Библиотека ARIMA - авторегрессионная модель проинтегрированного скользящего среднего

Источник: http://www.nickart.spb.ru/analysis/index.php

ARIMA - авторегрессионная модель проинтегрированного скользящего среднего

Допустим, Вы изучаете, как работает так называемое "сарафанное радио", т.е. как Ваши клиенты невольно распространяют Вашу рекламу. Покажем возможности применения моделей ARIMA на этом примере:
Введем следующие обозначения
x(t) - объем заказов за t -й месяц
x(t-1) - объем заказов за (t -1)й месяц
e(t-1) - отклонение прогноза в предыдущем периоде от фактического объема заказа прошлого месяца
Оценим с помощью метода наименьших кварадтов модель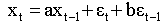

подставим оценки коэффициентов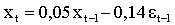

полученные результаты позволяют нам сделать следующий вывод:
При прочих равных, эффект сарафанного радио увеличивает количество клиентов в среднем на 5% в месяц, а отклонения прошлого периода, не учтенные этой моделью входят с коэффициентом 0,14. Что это за отклонения, и зачем они нужны? Вспомним пример о маркетинговой акции и включим в число объясняющих переменных фактор budget, обозначающий величину бюджета отдела продаж.
Рассмотрим новую модель

Теперь переменная x(t-1) интерпретируется по-прежнему, budget мы обозначаем как вклад текущего бюджета в приток новых клиентов, а e(t-1) заслуживает отдельного внимания.

Допустим, в прошлом периоде мы провели широкую рекламную кампанию, но по какой-то причине покупатели начали приходить только сейчас. Таким образом, в прошлом месяце наш фактический поток клиентов окажется ниже прогноза (думали, что придут сразу), а в текущем месяце мы получим поток "внеплановых клиентов". Коэффициент "-0,79" позволяет перенести 79 процентов отклонений прошлого периода (непришедшие клиенты) на текущий месяц. Такая модель позволяет предсказать аншлаг, имея в распоряжении лишь данные об отклонениях прошлого месяца.

Обозначается рассмотренная спецификация как ARMA(1,1), где (1, ) - количество лагов переменной, а ( ,1) - количество лагов "ошибки". Очень высокие порядки (сумма первого и второго параметров модели) на практике не встречаются, как правило, в хорошей модели это не больше 4-х.

При применении модели надо помнить о границах применимости и предпосылках использования подхода. К примеру, нестационарность рассматриваемых переменных приведет к ошибочным результатам. В этой ситуации рекомендуется использование моделей корректировки отклонений (ECM)

ECM - модель корректировки отклонений

Возвратимся к предыдущему примеру. Последнее замечание указывает на некорректность оценивания в случае, когда переменные обнаруживают нестационарность. Нестационарность достаточно хорошо можно обнаружить, используя графики. Существуют также и строгие критерии. Если сам процесс нестационарен, а его приращения стационарны, то говорят, что он интегрируем первого порядка.
Итак, вооружившись необходимой теорией, перейдем к практическим задачам. Допустим, мы рассматриваем, как влияет температура воздуха на спрос на наш товар (мороженное, купальники и т.п.). Если мы определили, что спрос на продукцию и температура нестационарны (это, скорее всего, именно так), а интегрируемы первого рода, то можно построить следующую модель:
Пусть
x - спрос на продукт
p - температура воздуха
тогда модель будет иметь вид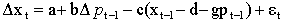

Оценим коэффициенты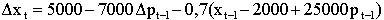

Поясним, что обозначают полученные результаты:

при прочих равных, вне зависимости от изменения температуры воздуха, прирост спроса летом составляет около 5 тыс. единиц в неделю;
снижение температуры воздуха на градус, при прочих равных приведет к росту в продаж продукции на 7000 единиц;
увеличение на 1000 разницы приведет к снижению продаж на 700 на этой неделе.

Последнее выражение и называется, собственно, моделью корректировки отклонений. Ее суть заключается в том, что если модель хорошая, то превышение плана сегодня, при прочих равных, скорее всего, выльется в небольшое снижение факта завтра, и наоборот.

VAR - Векторная авторегрессионная модель

Допустим, мы анализируем изменение во времени таких показателей предприятия, как чистый денежный поток, объем инвестиций, и объем продаж. Очевидно, что показатели взаимосвязаны между собой и зависят не только друг от друга, но и от своих предыдущих значений. Будем рассматривать модель с 2-мя лагами.
В предыдущих разделах мы рассматривали модели, так или иначе связанные с множественной регрессией. Предположим теперь, что в качестве зависимой переменной берется вектор, состоящий из различных показателей, а объясняющими переменными являются его лаги и константа. Поясним на примере:

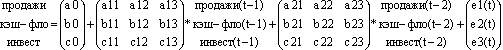
Коэффициенты в этой модели допускают следующую интерпретацию:
a11 - влияние "вчерашних" продаж на продажи сегодня;
b11 -влияние "вчерашних" продаж на денежный поток сегодня;
c11 - влияние "вчерашних" продаж на инвестиционный поток сегодня;
a12 - влияние "вчерашнего" денежного потока на продажи сегодня.

Как правило, в моделях такого рода используются предположения о структуре взаимосвязи между переменными, т.е., условно говоря, если мы продаем товар в рассрочку с периодом в месяц, навряд ли сегодняшние объемы сильно повлияют на текущий инвестиционный бюджет. Можно также предположить, что инвестиционные проекты начинают влиять на продажи, в среднем через два месяца, после начала финансирования. Такое предположение означает, что коэффициент a13 равен нулю. Обратим внимание на некоторые особенности модели: это не просто несколько авторегрессионных моделей, оцененных вместе. VAR модели позволяют исследовать не только влияние лагов на текущие значения переменных, но и их совместное изменение. Подход имеет ряд проблем - как вычислительного, так и концептуального характера. Основные из них - это

проблема идентифицируемости ограничений (в нашем примере мы заранее предположили а13=0, что позволяет идентифицировать влияние денежного потока и инвестиционного потока предыдущего периода на текущие показатели). Введение в модель таких предпосылок требует, по меньшей мере, хорошего экономического обоснования.
квадратичная зависимость количества коэффициентов от размерности модели. Здесь следует подчеркнуть недостаточную ценность для прогнозов моделей с числом переменных ниже 4-х.

Обратим внимание на то, что прежде чем давать интерпретацию коэффициентов, полученных при оценивании в рамках VAR подхода, рекомендуется провести тест причинности по Грейнджеру, а также проверить, не обнаруживают ли необъясненные моделью отклонения свойств гетероскедастичности и автокорреляции.

VECM - Векторная модель корректировки отклонений

VECM представляет собой аналог модели корректировки отклонений, использование которого основано на VAR-подходе