 (5)
(5)
МАТРИЧНЫЕ ПОСТРОЕНИЯ В Кi- ЗНАЧНОЙ ЛОГИКЕ.
2000 г. М. Я. Эйнгорин.
Нижний Новгород. Институт Прикладной Физики РАН.
URL: http://www.uic.nnov.ru/~emy/mnogolog.html
Работа относится к разделу многозначной логики. Рассматриваются построения и преобразование матричных логических структур с различным базисом по каждому из переменных. Для расширения функциональных возможностей вводятся понятия обобщенной и полной инверсий. Показана возможность значительного расширения функциональных свойств за счет управления законами инверсии. Смена инверсии практически означает смену логики. Приводятся примеры. На базе латинских гиперпрямоугольников и дизъюнктивных нормальных форм строятся матрицы наборов ортогональных функций. Построение обеспечивает синтез практически любых матриц функций многозначной логики. Приводятся методы построения полных ортогональных наборов функций и матриц. Работа представляет интерес для специалистов в области математической логики, микроэлектроники, молекулярной биологии, компьютерной технике и цифровым системам управления.
Введение. Значительными темпами развивающаяся цифровая техника практически вся строится на базе двухзначной математической логики. Это ни всегда экономично, но средства микроэлектроники и ее достижения, в настоящее время, слабо считаются с этими потерями. Современная микроэлектроника показала и еще одну важную тенденцию. Существенное значение при синтезе больших устройств, играет возможность их матричного выполнения на регулярных структурах. При этом существенно меньшее значение играет минимизация, которая была важна на ранних стадиях развития, когда приходилось считаться с каждым лишним контактом реле, электронной лампой, диодом или транзистором. Существенно большее значение приобретает "глобальная" минимизация на уровне больших функциональных узлов и блоков. К сожалению, твердотельная микроэлектроника подходит к своему естественному пределу по размерам кристалла, ширине соединительных шин, запаздыванию в них сигналов и мощности, выделяемой на одном кристалле. Возможности повышения рабочей частоты, увеличения плотности размещения элементов с их миниатюризацией и увеличение (уменьшение) размеров кристалла скоро будут исчерпаны. Даже наращивание разрядности имеет свой логический предел. Слишком быстро прогресс приближается к тупиковому состоянию. Необходимы новые пути решения чрезвычайно важной для человечества задачи построения быстродействующих и интеллектуальных помощников и партнеров, само развивающихся и самовоспроизводящихся, под контролем человека, партнеров. В настоящее время видится ряд путей преодоления этих трудностей.
Во первых, решение задачи лежит в развитии конвейерных вычислительных систем, что в значительной степени определяется развитием и применением сетей.
Во вторых, далеко не исчерпаны новые перспективные направления в физике и, следовательно, в микроэлектронике, которые обеспечат новые пути развития.
В третьих, должны быть найдены новые пути развития запоминающих устройств, как главного компонента цифровых систем управления.
В четвертых, это исследования в области организации логических структур и памяти, близких к созданным природой. В этом направлении еще предстоит большая совместная работа биологов, молекулярных биологов и кибернетиков.
В пятых, не следует забывать и микробиологический путь, как главное перспективное направление будущего.
В шестых, решение задачи дальнейшего прогресса в цифровой технике может быть найдено в использовании несколько "забытой" многозначной логике [1; 2; 3] с ее богатыми возможностями представления и переработки информации.
Многозначная логика предоставляет более широкие возможности для синтеза управляющих и запоминающих устройств, чем двухзначная, являющаяся ее малой частью. Решения задач на базе многозначной логики могут быть часто значительно компактнее изящнее и шире в части функциональных возможностей.
Последнее направление близко к четвертому и пятому путям. Природа для записи программной, генетической, информации использует четырехзначный базис, а синтез белков по генетическим программам ведется на базе двадцатизначного базиса. Природа чаще всего выбирает оптимальный путь решения своих задач, что должны помнить мы - люди в своих разработках. Поэтому рассмотрим шестой путь, всегда имея в виду четвертый и пятый пути.
Для возможности применения многозначной логики "сегодня", ее необходимо привести к виду, удобному для моделирования на тех отработанных микроэлектронных структурах достижения, в области которых и обеспечило современное развитие. Только это может привлечь внимание специалистов в области микроэлектроники и обеспечить достаточно быстрый переход и прогресс. Безусловно, применение многозначной логики потребует новых решений в области принципов работы элементов и схемотехнических решений.
В настоящей работе сделана попытка "приблизить" многозначную логику к современной микроэлектронике.
Не нарушая общности, будем иметь в виду "пространственное" представление информации, которое приближает ее к представлению, привычному для двоичной логики, легко реализуемой средствами современной микроэлектроники. В современной микроэлектронике весьма широко используются дешифраторы, а это уже не что иное, как пространственное представление многозначной информации. В настоящей работе построение будем вести в виде функциональных матричных блоков, удобных для моделирования и применения. При этом хотелось бы вновь отметить, что главным источником прогресса является синтез широких классов запоминающих устройств, особенно многофункциональных [4], с возможностью "ухода" от электромеханики. Синтез многоустойчивых элементов и устройств приводится в работах [5; 6].
Постановка задачи. Расширить математический аппарат многозначной логики, для построения матричных структур с естественной "привязкой" к базису каждого из переменных, расширить функциональные возможности блоков с тем, чтобы дать исследователям и разработчикам возможность использования достижений современной электроники и применить их к новым перспективным разработкам. Дать в руки биологов, и специалистов других направлений математический аппарат для анализа, толкования и исследования сложных систем.
Пусть Xi - независимое многозначное переменное, Xi [0,(ni - 1)], i = [1,N].
(Заменим привычное для заголовка "Кi", на привычное для содержания "ni").
Не меняя общности рассуждений, примем, что:
n1 ≤ n2 ≤ . ≤ ni ≤ . ≤ nN , в силу чего: Xi [0,(nN -1)]. (1)
Для дальнейших функциональных построений воспользуемся базовых набором: Max(Xi¨), Min(Xi¨), и инверсией, для чего введем обобщенное ее понятие.
Запишем базовую таблицу ni для построения ортогональных латинских квадратов (ОЛК). В ней по вертикали расположим по ni чисел от 0 до (ni - 1), повторив столбцы ni раз. На основе полученной базовой таблицы могут быть построены до (ni - 1) ОЛК, в зависимости от свойств чисел nί . В большинстве практически важных случаях, число ОЛК равно (ni - 1). В данной работе не будем останавливаться на способах построения полной системы ОЛК. Для построения их воспользуемся [7; 8; 9]. Перенумеруем ОЛК через Wi = [1,ni-1], i = [1,N]. В каждом построенном ОЛК будет по ni одинаковых чисел wi ε[0,(ni - 1)], расположенных в различных строках и столбцах.
Назовем набор чисел (Wi, wi) - характеристическим.
В каждом ОЛК введем координаты абсцисс Xi и ординат Zi . Введем понятие "латинского преобразования" (LP) и обозначим его через:
L(Wi ,wi , Xi ) (2)
и
L(Wi ,wi ,Xi ≈ Zj ), (3)
при Wi ,wi , Xi , Zj ε (0,ni -1).
Выражение (2) будет означать, что оно принимает значение ординаты Zj в латинском квадрате с номером Wi при пересечении значения независимой переменной Xi с заданным числом wi .
Выражение (3) будет означать, что некоторое число принимает значение, равное Рi, при соответствии независимой переменной Xi и ординаты Zj в латинском квадрате Wί на заданном числе wί .
На базе (2) (положив Zj = NXi) запишем обобщенное выражение для "одноканальной" инверсии многозначной логики в виде:
NXi = L(Wi ,wi ,Xi ) (4)
Обобщенное выражение (положив Zj = σij) для "пространственной" инверсии запишем в виде:
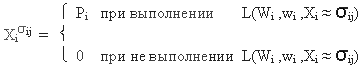 (5)
(5)
При этом в зависимости от принятой системы, Pi [1,(ni - 1)].
Выражения (4) и (5) значительно расширяют понятие инверсии, число которых формально может быть Ňi ≤ ni . (ni - 1), для каждого i = [1,N]. Каждое из переменных Xi может иметь "свой" набор* возможных инверсий. Поэтому общее число комбинаций инверсий может достигать значения:
____________________
* В более общем случае независимые переменные Xi = |1,ni| могут принимать значения Xi = |a1i,ani|, для всех i = |1,N|. В этом случае не работает закон коммутативности, происходит переход к позиционной системе.
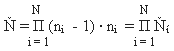 (6)
(6)
Если функции Max и Min справедливы для любой логики, то инверсия - это функция, принципиально меняющая логику. В связи с чем, выбор той или иной функции инверсии из (6), является фактически сменой логики.
Приведем пример. Пусть ni = 5. Запишем "базовую" таблицу для построения ОЛК. Так как 5 - простое число, то общее число ОЛК W = 4. Построим их на основе, например, работы [7].
 (7)
(7)
Если для (4) в (7) принять Wi = 1 и wi = 3 , то получим известное выражение
отрицания в многозначной логике "циклического" типа [1], вида:
NXi = (Xi + 1) mod ni .
При Wi = 4 и wi = 0 , получим так - же известное выражение: NXi = (ni - 1) - Xi ,
названное в литературе "отрицанием Лукашевича". Оно известно, как же, как "зеркальное отображение" инверсии циклического вида. Но, видимо, ближе к "зеркальному отображению" лежат отрицания с параметрами Wi = 4 ,wi = 1 или Wi = 4 , wi = 4 .
Если для выражения (5) принять Wi = 1 ,wi = 4 и Pi = (ni - 1), получим известное выражение для многозначной инверсии, вида:
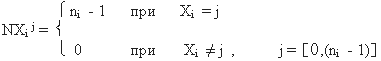 (8)
(8)
Приняв Pi = 1, получим известное выражение для многозначного отрицания [1, 5].
Аналогично тому, как введена обобщенная инверсия для независимых переменных, введем функциональную инверсию (ФИ) для функций fj(Xi¨) при i = [1,N], j Î Mj . Пусть промежуточный набор функций fj(Xi¨) некоего функционального построения таков, что всегда лишь одна функция из набора Mi равна P, остальные равны нулю. Тогда, обобщенная пространственная ФИ для набора Mj запишется в виде:
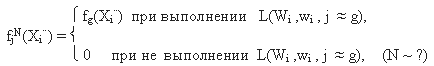 (9)
(9)
_______________
*) Существует (ni - 1) ОЛК для простых чисел ni , степеней простых чисел, произведения степеней простых чисел [7; 8; 9]. Для других чисел, число ОЛК может
быть равно или меньше (ni - 1). Так для n = 6, существует лишь три ОЛК.
При этом, на оси абсцисс в латинском квадрате LP откладываются все функции
fj(Xi¨), а по оси ординат fg(Xi¨).
Заметим, что если выражение для обобщенной многозначной инверсии (4), при моделировании на конкретных физических элементах, дает одиночный многозначный канал, то выражение для той же многозначной инверсии (5), дает
"пространственный" канал. При этом в каждом из "пространственных" каналов многозначное переменное принимает два значения. Последнее обеспечивает легкость моделирования функций многозначной логики методами современной
микроэлектроники, сохраняя определенные ее преимущества.
Введем понятие полной инверсии. Под полной инверсией будем понимать инверсию от всех переменных конституанты, функции или группы функций, выполненную в соответствии с выбранными характеристическими числами для каждого из переменных. Аналогичное понятие было введено для систем логических уравнений [5]. В связи с введением обобщенной и полной инверсий, связанных с характеристическими числами, возникает проблема циклов при взятии инверсии в многозначной логике.
Под циклом инверсии будем понимать число последовательно взятых инверсий, при котором переменное, конституанта, функция или система функций переходит в себя. Число ni можно представить в виде произведения простых сомножителей, вида: ni = Пji gj при ji = (1, hi), где: gj - простые числа. В зависимости от первоначального значения переменного при последовательности взятых инверсий, оно может принимать только gi из ni возможных значений и только в одном из циклов hi. Принципиально для одного переменного ni могут существовать циклы с различным числом простых сомножителей. В этом случае и число циклов будет различно.
Наибольший практический интерес представляют полные инверсии над системами функций с малым периодом: два и три при равных циклах.
Известно [1; 2; 3], что для элементарных функций и их сочетаний имеют место следующие свойства, которые верны и для многозначных функций переменных оснований:
1) Свойство ассоциативности: (X1 о X2) о X3 = X1 о (X2 о X3), (10)
2) Свойство коммутативности: (X1 о X2) = (X2 о X1),
3) Свойство дистрибутивности: (X1 v X2) X3 = (X1 X3) v (X2 X3), (X1 X2) v X3 =
= (X1 v X3) (X2 v X3).
4) Правило введения переменной: X1 = X1[I0(X2) v .v In-1(X2)],
5) Правило исключения переменных:
X = 1.I1(X) v 2.I2(X) v . v (n -
1).In-1(X), при 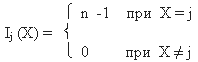
6) Правило упрощений:
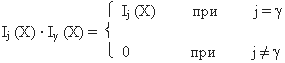
Отметим еще ряд свойств, справедливых для многозначной логики переменных
оснований: (n - 1) X = X , 0 X = 0, (n - 1) v X = (n - 1), 0 v X = X .
Указанные свойства сохраняются и для введенной функции обобщенной инверсии.
В соответствии с поставленной задачей, рассмотрим матричные принципы построения функциональных блоков на базе многозначной логики. Это целесообразно для упрощения перехода современной микроэлектроники к построению больших функциональных устройств на ее основе.
Будем строить функции многозначной логики переменных оснований (МЛПО), с
учетом (1), на основе совершенных нормальных дизъюнктивных [1; 2; 3; 6] форм (СНДФ), приняв за базисный набор Max, Min и инверсию по (4) и (5). Если
функции Max и Min будем относить ко всем переменным, то функцию инверсии по (4) и (5), будем относить к каждому переменному Xi "персонально". То есть каждое переменное Xi, в общем случае, может иметь "свои" характеристические
числа (Wi ,wi), i = [1,N] и, "свой" закон инверсии. Положим в (5) Pi = (nN - 1).
Тогда, выражение для пространственной инверсии (5) будет иметь [1] вид:
 (11)
(11)
В этом случае элементарную конституанту МЛПО от N независимых переменных запишем в виде:
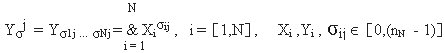 (12)
(12)
Очевидно, что число полных и различных конституант K от N переменных равно:
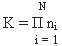 (13)
(13)
Охарактеризуем каждую конституанту (11) набором:
( σ1j, σ2j, . , σij, ., σNj ), (14)
число которых, также определяет выражение (13).
Сформулируем некоторые определения:
1. Назовем многозначную функцию fd(Xi¨) , записанную в СНДФ и содержащую
ni различных конституант вида (12) с разложением по независимой переменной Xi , элементарной функцией
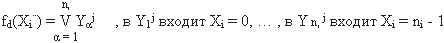 (15)
(15)
2. Две элементарные функции fd(Xi¨) и fg(Xi¨) назовем независимыми, если они не
содержат ни одной совпадающей конституанты Yαj .
3. Две элементарные функции fd(Xi¨) и fg(Xi¨) назовем ортогональными, если они имеют не более одной общей конституанты Yαj .
4. Назовем все возможные независимые элементарные функции с разложением по одной из переменных, например ni , - базовым по ni набором |F|i .
5. Назовем базовый набор |F|i элементарных функций - координатным базовым
набором |F|i0 , если все его элементарные функции (15) для i = [1,N] вырождаются в отдельные конституанты вида:
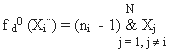 (16)
(16)
Число функций или конституант (16) в |F|i0 равно:
 (17)
(17)
Рассмотрим наборы (14) как позиционные числа с переменным основанием счисления в каждом из разрядов. Пусть основания систем счисления соответственно равны: n1, n2, . ,ni , . , nN . Составим таблицу, в которой по горизонтали расположим ni наборов при i = 1 из (13), а по вертикали (17) наборов. Пусть, так же справа в каждом наборе расположены "старшие" разряды, а слева, "младшие". В каждом из столбцов вертикально расположим "перебор" всех наборов с i = 2, до i = N. Слева в крайнем столбце в наборе будут стоять нули, справа в последнем наборе будут стоять (n1 - 1). Таблицу можно построить и иначе.
Обозначим полученную таблицу через |G|10 . Эта таблица является базовой для построения максимальной системы ортогональных латинских гиперпрямоугольников. Не нарушая общности дальнейших рассуждений, для простоты, примем, что все ni взаимно просты. Для большинства важных случаев и не взаимно простых ni , ниже сформулированные результаты будут верны [7; 8; 9].
Заменим в полученной таблице наборы (14) на эквивалентные им конституанты (12), получим таблицу |K|10. Поставим в таблице |K|10 между конституантами каждой строки знаки дизъюнкции, тогда каждая строка будет соответствовать элементарной функции (15). Полученную таблицу обозначим через |F|10 . В этом случае вся таблица будет соответствовать координатному базовому набору функций с одной конституантой в каждой элементарной функции, и числом переменных N - 1. Переменную n1 заменит константа (n1 - 1).
На основе выполненного построения, докажем следующее:
Теорема. Для любой многозначной логики переменных оснований G с аргументами Xi , i = [1,N], при 0 ≤ Xi ≤ (ni - 1), ni ≤ ni+1, и инверсии с характеристическими числами (Wi ,wi) , можно построить
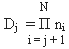 (18)
(18)
базовых наборов |F|j ортогональных элементарных функций, состоящих из nj конституант, с числом независимых элементарных функций в каждом наборе:
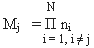 (19)
(19)
Доказательство. Для построения возьмем координатную базовую таблицу конституант |K|10. Каждая строка таблицы соответствует элементарной функции (15) МЛПО. Очевидно, что исходная таблица |K|10 даст вырожденные элементарные функции, ибо каждая строка таблицы фактически является разложением одной и той же конституанты по всем значениям переменной n1. Для построения всех базовых наборов |K|jη, 1 ≤ η ≤ Di , удовлетворяющих, для элементарных функций определениям 2) и 3), воспользуемся методами построения латинских гиперпрямоугольноков, изложенными в [7; 8; 9].
Для сформулированного в теореме случая взаимно простых ni , при i = [1,N], применим метод "кручения" или "сдвига" [7]. В результате его использования на первом шаге, получим:
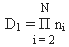 (20)
(20)
базовых наборов таблиц |K|1η, (1 ≤ η ≤ D1), каждая из которых содержит:
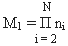 (21)
(21)
строк, соответствующих (15) независимым элементарным функциям, имеющим по n1 конституант. При этом в каждой из конституант, слева направо будут стоять переменные Xi от 1 до N, а сами переменные могут иметь значения от 0 до (ni - 1).
На втором шаге координатную базовую таблицу |K|10 преобразуем так, чтобы разложение элементарных функций в |F|2 шло по n2 . Вновь применения метода "сдвига", получим:
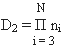 (22)
(22)
и 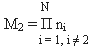 (23)
(23)
Действуя аналогичным образом, на j - ом шаге, получим:
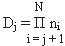 (24)
(24)
базовых таблиц конституант |K|jη (1 ≤ η ≤ Di), или соответствующих им базовых наборов элементарных функций |F|jη , с числом независимых ЭФ в каждом наборе:
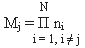 (25)
(25)
и числом конституант nj в каждой элементарной функции.
Продолжая аналогичные процедуры, на (nN - 1) и nN шагах получим число базовых ортогональных таблиц, соответственно:
DN-1 = nN и DN = 1, (26)
Число независимых элементарных функций в таблицах последних шагов будут иметь соответственно следующие значения:
N N-1
MN-1 = П ni и MN = П ni (27)
i = 1, i ≠ N-1 i = 1
N
При этом в (26) для DN принято, что П ni = 1.
i = N+1
В силу способа построения таблиц |K|jη и, соответственно, наборов таблиц функций |F|jη , в каждой таблице |F|jη элементарные функции будут независимы, а в различных таблицах |F|gη и |F|sβ , при g ≠ s - ортогональны.
Сравнивая выражения (24) и (25) с выражениями (18) и (19) в формулировке теоремы, можно заключить, что теорема доказана.
Следствия, вытекающие из способа доказательства теоремы.
1) В каждом базовом наборе функций |F|jη (24), одна из них координатная базовая таблица, начиная с |F|10 от |K|10, взятой за исходную (1 ≤ j ≤ N).
2) Элементарные функции всех координатных базовых наборов |F|j0 для j = [1,N] -
вырожденные и представляет собой одну конституанту, в которой переменное Xi заменено соответствующим значением (ni - 1).
3) Любые две элементарные функции любого базового набора - независимы.
4) Любая элементарная функция базового набора |F|gη имеет не более одной
совпадающей конституанты c элементарной функцией набора |F|sβ, при g ≠ s.
5) Для каждой элементарной функции базового набора |F|gη найдется точно ng
элементарных функций базового набора |F|sβ, с которыми, первая имеет совпадающие конституанты (по числу конституант в ЭФ |F|gη), при g ≠ s и Dg ≤ Ds.
6) Каждая конституанта (12) входит лишь в одну элементарную функцию базового набора |F|gη , g = [1,N].
7) Дизъюнкция элементарных функций любого базового набора |F|gη независима
с ЭФ, не вошедшими в нее, из того же базового набора.
8) Конъюнкция любых ЭФ базового набора |F|gη , f u(Xi¨) & f p(Xi¨) ≡ 0, при u ≠ p.
9) Дизъюнкция всех элементарных функций любого базового набора |F|jη ,
j = [1,N] представляет собой полную дизъюнктивную нормальную форму:
Fj(Xi¨) = V fd(Xi¨) = (nj - 1), для j= [1,N]. (28)
По всем Mj
11) Любая функция fd(Xi¨) Ki - значной логики i = [1,N] может быть получена путем дизъюнкции элементарных функций любого базового набора |F|jη и удаления отдельных конституант из них.
12) Для синтеза набора требуемых функций, может быть взят любой наиболее подходящий из базовых наборов (24), как по числу конституант в элементарных функциях ni , так и по базовому набору в пределах (25).
13) Расширение возможностей синтеза может быть получено за счет одновременного использования нескольких базовых наборов ЭФ. В случае наличия в них одинаковых конституант, совпадающие будут поглощены.
14) Из доказательства теоремы и (24) следует, что число базовых наборов для разных i = [1,N] различно. Для получения требуемого числа ортогональных базовых наборов функций при конкретном ni , возможно произвести подстановку:
n1 n2 . ni . nN-1 nN
nα1 nα2 . nαi . nαN-1 nN (29)
и повторить построение.
15) Максимально, общее число ортогональных наборов элементарных функций
равно: 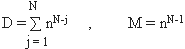
16) При всех равных ni = nj , i,j Î [1,N],
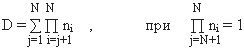 (30)
(30)
Очевидно, что при n = 2 для всех i = [1,N], теорема и все следствия - справедливы.
Функции, построенные согласно следствиям 11 - 13, могут быть использованы как функции многозначной логики с переменным основанием; в виде равенств, разрешенных относительно констант; в виде систем уравнений функций; систем уравнений, разрешенных относительно переменных или в виде систем эквивалентности многозначных функций и некоторого набора констант, возможно и, не входящих в наборы значений переменных.
Рассмотрим простейший пример. Пусть n1 = n2 = 2, N = 2. Выберем избыточный базис Max(X1,X2), Min(X1,X2) и инверсию в виде (9), приняв p = (ni - 1) = 1. Формально выберем характеристическое число для формирования закона инверсии. Для этого построим латинский квадрат на основе базового.
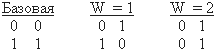 (31)
(31)
Базовая таблица и таблица W = 2 являются координатными, в силу чего рассматривать их не будем. Для n1 = n2 = 2 существует один ОЛК, поэтому рассмотрим W = 1. Выберем характеристическое число w = 0. В силу простоты примера, "координаты" вводить не будем. В этом случае, при Х = 0, Х0 = 1 и, наоборот, при Х = 1, Х0 = 0. Это обычный закон инверсии для логики с n1 = n2 = 2.
Конституанты для нашего примера будут иметь вид: Х11Х21, Х11Х20, Х10Х21, Х10Х20, или, учтя коэффициенты над переменными, можем записать первую координатную базовую таблицу |G|10 для построения ОЛК и базовых ортогональных наборов элементарных функций:
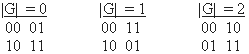 (32)
(32)
Таблицы |G|10 = 0 и |G|20 = 2 соответствуют базовым координатным наборам и, при переходе к |F|10 и |F|20 , вырождаются в функции f10 = X10, f20 = X11, f30 = X20 и f40 = X21. Функции же базовой таблицы |G|11 = 1 при переходе к |F|11 , дают две не тривиальные независимые функции f11 = X10 X20 V X11 X21 и f21 = X11 X20 V X10 X21 . При этом, f21(Xi¨) является элементарной функцией суммирования по mod 2, а элементарная функция f11(Xi¨) является ее инверсией.
Очевидно, что более подробное исследование элементарных функций и их комбинаций при ni ≥ 2, N ≥ 2 и различных характеристических числах (Wi ,wi),
i = [1,N], даст много красивых и интересных решений для синтеза и преобразования функций многозначной логики переменных оснований.
Геометрическая модель. Независимые переменные Xi , i = [1,N] представляет собой координатные направления N - мерного пространства, в котором размещен гиперкуб со сторонами nj , j = [0,(nj - 1)].
В каждой точке дискретного N мерного гиперкуба расположена конституанта (12), с входящими в нее значениями (14) N переменных (1), соответствующими их значениям по координатным направлениям. (При этом, следует заметить, что запись каждой конституанты становится позиционной. Следствием этого является неработоспособность законов ассоциативности, коммутативности и дистрибутивности (10). Последнее связано с тем, что положение каждой конкретной конституанты, в геометрической модели, зависит от расположения в ней переменных). Базовые наборы |F|gη объединяют знаком дизъюнкции те конституанты (12) гиперкуба, которые соответствуют строками ЭФ этих наборов. N ортогональных базовых наборов элементарных функций, расположенные по N координатным направлениям, являются вырожденными (15) и содержат по одной конституанте, переменное данного направления в которых заменено на (ni - 1). Всего в гиперкубе конституант может быть "размещено" для каждого i = [1,N] по (Dg - 1) (24), не вырожденных БНЭФ с числом ортогональных ЭФ в каждом (25) и числом конституант в ЭФ ni . Каждый базовый набор функций |F|gη из (24) строится на базе одной таблицы латинского гиперпрямоугольника.
Микроэлектронная модель. На базовом кристалле сформирована матрица элементов "И" размером n1 x П ni , для i = |2,N|. В матрице каждое значение переменного Xi , для σij = [0,(ni - 1)] соединены отдельными шинами и образуют пространственное переменное Xi . В каждом пространственном переменном ni шин. Число пространственных групп шин N. Над базовым кристаллом (или внутри него) над матрицей из ni элементов "И" расположены шины "ИЛИ", объединяющие "лежащие" под ней элементы "И" в соответствии с независимыми ЭФ одного из базовых наборов функций |F|gη . Это ортогональный набор из (25) элементарных функций. При необходимости, над той же матрицей элементов "И" через дополнительные элементы объединения "ИЛИ", могут быть "сформированы" другие ортогональные наборы элементарных функций |F|hβ в соответствии с (20) - (27). Для получения более сложных функций из ЭФ, они объединяются в дизъюнкции простым соединением шин. Для более рационального использования площади кристалла, матрица "ИЛИ" может быть сформирована и иначе. Необходимо заметить, что конфигурация шин для элементарных функций и новых ортогональных базовых наборов, будут "ажурнее", чем для "первого координатного" построенного набора с "горизонтальными" шинами.
Блок - схемы устройств на базе МЛПО. Рассмотренные логические построения базируются на N независимых переменных, каждое из которых имеет значность ni , при i = [1,N] . Для каждого значения ni может быть построено Di базовых наборов |F|iη (24) из Mi элементарных функций (25), имеющих по ni конституант вида (11) каждая. Для заданных значений независимых переменных в каждой базовой таблице |F|iη одна элементарная функция имеет значение равное единице. Для формирования функции отличной от элементарной, может быть использовано объединение ЭФ одного или нескольких наборов |F|iη .
В работе было введено обобщенное понятие инверсии (4),(5), поэтому, число возможных "комбинаций" инверсий составит (6). В результате последнего появляется дополнительная и широкая возможность управления ортогональными базовыми наборами - матрицами через характеристические числа (Wi ,wi), меняя логику самой переработки информации. Дополнительное управление по обобщенным инверсиям может быть как в блоках входных переменных, так и на выходах блоков |F|iη , применяя обобщенную функциональную инверсию (10).
Передача информации от ее источника к блоку многозначной переработки (при пространственном представлении) может быть выполнена в "свернутом" двоичном или ином коде. Этим может быть сокращено число шин передачи информации, что важно для практических применений. То же, если приходящая информация представлена в пространственном или двоичном коде, а блок многозначной переработки информации является одноканальным по каждому из независимых переменных.
Дополнительно следует отметить следующее. При равных ni = nj для всех i,j Î [1N], каждая из ортогональных базовых таблиц - матриц обеспечит различные алгоритмы переработки информации, поступающей от независимых переменных. Для ряда технических приложений такая переработка информации представляет определенный практический интерес. Кроме того, на базе ортогональных базовых таблиц могут быть построены оптимизированные более функционально сложные образования. Дополнительное "управление" по параметру "инверсия", меняющее в целом логику переработки информации, значительно расширит функциональные возможности синтезируемых устройств.
В качестве одного из примеров можно привести многомерный дешифратор [10]. В нем N = 2, n1 = n2. Над матрицей конституант сформированы базовые наборы матриц функций |F|11, . , |F|1K, каждая из которых содержит по ni независимых ЭФ. Все функции разных матриц - ортогональны. Каждый из выходных ортогональных наборов |F|1j преобразуется "своим" законом обобщенной ФИ (10). В результате дешифратор имеет два входных набора управления X1, X2 и набор управления по ФИ. Выходными являются K наборов |FN|1j при j = |1,K|.
Дешифратор может управлять трехмерным устройством, выполненным в виде набора плоских двухмерных матриц, с частичным возбуждением на не выбранном мажоритарном элементе не более 2/K. Выбранный элемент имеет сигнал выборки K/K=1. Дешифратор значительно экономичнее традиционных.
Заключение. В результате выполненных построений имеет место следующее:
Показана возможность широкого применения комбинаторных методов (латинских гиперпрямоугольников, неполных уравновешенных блок-схем) для синтеза функций и матриц в многозначной логике.
За счет введенного более широко (обобщенного и полного) понятий инверсии, получена возможность смены логики функционального преобразования информации, смены логики "работы" матриц, что во много раз расширяет функциональные возможности синтезируемых устройств.
Любая из базовых ортогональных наборов таблиц обеспечивает синтез любых, необходимых в данной задаче, функций в виде СНДФ (СНКФ).
Элементарные функции и их объединения, в пределах одной ортогональной таблицы, не имеют избыточности и обеспечат синтез, минимальных схем.
Разработчик имеет возможность подобрать оптимальный набор стандартных элементарных ячеек (элементарных функций) путем выбора базовой таблицы из значительного их набора, построенного в процессе доказательства теоремы.
Разработчику предоставлена возможность "регулировать" число и состав ортогональных базовых таблиц с заданным числом конституант в элементарной функции.
Синтезируемые функциональные устройства, в виде матриц, принимают "стандартизованные" размеры, что важно для синтеза больших интегральных схем.
Показана возможность построения функциональных матричных устройств, которые могут реализоваться на базе современной микроэлектроники.
Синтез устройств на базе многозначной логики может свестись к синтезу привычных устройств на базе двухзначной логики, по отработанным технологическим методикам и даже схемам.
Любое устройство, работающее по двузначной логике и имеющее выход с дешифратора и вход с него, может рассматриваться, как устройство с многозначными переменными вида (10). Необходимо лишь дальнейшую "переработку" информации вести по закону той или иной многозначной инверсии.
Настоящая работа доложена на XII Международной конференции "Проблемы теоретической кибернетики" 17 - 22 мая 1999 года.
Литература.