|
Cauchy problem for the ordinary differential equation of 1-st order is described by the formula (4.1).
 (4.1)
For the numerical solving of Cauchy problem it is necessary to calculate set of values of approximated function on
the specified interval. The infinite set of points of an interval is replaced by the final cluster. Values of unknown function
are being recalculated in points of the grid that replaces initial interval. Points of the grid are placed to the
equally-spaced positions; distance between the neighbors forms a step
( ).
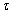The approximate solution is restored with the set accuracy which is defined by frequency of grid points and characteristics
of a numerical solving method [5].
Let the set M of points of a uniform grid {tm}, m = 1, M и tm = T
is divided on N the blocks (where
-
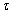is step size). Each block consists of k points of the finite grid. Thus, the total number of points of all blocks is multiple to the
total number of blocks.
Let n – number (index) of the block of a grid, i – number (index) of a point within the block and tn,i – a point
with number i in the block with number n. Characteristic points of the n-th block are:
- tn,0 - index point of the block which is not included in it;
- tn,k - final point of the block.
-
The scheme of subdividing into blocks for a single-step k-dotted method is shown on figure 4.1.
Figure 4.1 –Scheme of subdividing of initial interval into blocks for a single-step k-dotted method
The main feature of a single-step block method is ability of simultaneously calculation of k new values of required function.
Such computation independence allows performing of approximate solution simultaneous calculation in points of the block [5].
The equations for multistep difference methods for the block of k points are shown on figure (4.2). These methods are using
the calculated values of the approximate solution in m points previous the block. The given formula defines a single-step
k-dotted method [5].
 (4.2)
|
