В. Соловьев, А. Климович
Использование входных буферов ПЛИС в качестве элементов памяти конечных автоматов
Рассматривается новый подход к проектированию конечных автоматов на ПЛИС, когда входные буферы ПЛИС используются в качестве элементов памяти конечных автоматов. Конечные автоматы типа Мили, допускающие такую реализацию, получили название автоматов класса E, а конечные автоматы типа Мура - автоматов класса F. Описывается метод синтеза автоматов классов E и F. Результаты экспериментальных исследований предложенных методов в сравнении с традиционными подходами, реализованными в пакетах MAX+PLUSII и WebPack, показали высокую эффективность новых методов синтеза, которые позволяют уменьшить число используемых макроячеек ПЛИС, в среднем, в 3,5 раза, а для отдельных примеров - в 8–9 раз.
Введение
В [1] было рассмотрено использование триггеров выходных макроячеек ПЛИС в качестве элементов памяти конечных автоматов. Но входные буферы ПЛИС также часто содержат триггеры. Отсюда возникает вопрос, нельзя ли эти триггеры использовать в качестве элементов памяти при синтезе конечных автоматов? Оказывается, что можно, а структурными моделями таких конечных автоматов являются автоматы классов E и F, рассмотренные в [2].
На основании автоматов классов E и F в [2] предложено 8 различных структурных моделей, допускающих эффективную реализацию на ПЛИС: EI, E0, F0, EI0, EI’, FI’, EI0’ и FI0’. Для реализации этих моделей достаточно располагать только двумя методами синтеза: автомата класса E и автомата класса F. Другие модели строятся на основании структур автоматов классов E и F путём установки регистров на входе (EI), регистров на выходе (E0, F0), регистров одновременно на входе и выходе (EI0), защёлок на входе (EI’, FI’), а также защёлок на входе и регистров на выходе (EI0’, FI0’).
Структуры конечных автоматов классов E и F
Автоматом класса E (F) является автомат типа Мили (Мура), каждый входной набор которого совпадает с кодом следующего состояния. Это позволяет в качестве элементов памяти использовать триггеры входных буферов ПЛИС, а также исключить из структуры конечного автомата комбинационную схему, реализующую функции переходов [2]. Отметим, что значение каждой входной переменной всегда проходит через входной буфер ПЛИС, поэтому использование триггеров входных буферов в качестве элементов памяти конечного автомата не увеличивает стоимость реализации конечного автомата на ПЛИС.
Однако на практике не всегда наборы значений входных переменных могут выступать в качестве кодов внутренних состояний. Например, если число L входных переменных меньше значения intlog2M, где М - число внутренних состояний конечного автомата, или когда переходы в различные внутренние состояния конечного автомата инициируются одним и тем же набором значений входных переменных. С другой стороны, не всякая совокупность выходных наборов пригодна для кодирования внутренних состояний автомата: из условия детерминированности поведения конечного автомата коды различных состояний должны быть ортогональны между собой (по крайней мере в одном разряде иметь различные значащие значения). Во всех этих случаях в структуру автоматов классов E и F необходимо вводить дополнительные элементы памяти для различия кодов внутренних состояний.
Таким образом, наиболее часто реализуемые структуры автоматов классов E и F показаны соответственно на рис. 1а, б, где CL - комбинационная часть конечного автомата; RGI - входной буфер; RG - регистр дополнительных элементов памяти; X = {x1,...,xL} - множество входных переменных конечного автомата; Y = {y1,...,yN} - множество выходных функций (выходных переменных) конечного автомата; G = {g1,...,gL} - множество переменных, определяющих коды внутренних состояний, соответствующих входным переменным; D = {d1,...,dL} - множество функций возбуждения элементов памяти (переходов); E = {e1,...,eL} - множество переменных обратных связей.
Рисунок 1. Структуры конечных автоматов с входными буферами ПЛИС в качестве элементов памяти: а) автомат класса E (Мили); б) автомат класса F (Мура)
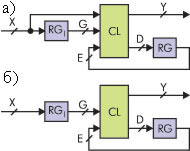
Отметим, что в структуре автомата класса E (рис. 1а) входной буфер имеет две связи с комбинационной частью конечного автомата: буферизированную (регистровую) и прямую (комбинационную). Это связано с тем, что в автоматах типа Мили (а автомат класса E является автоматом типа Мили) выходные функции непосредственно зависят от входных переменных. Поэтому для реализации автоматов класса E каждый входной буфер ПЛИС должен иметь две связи с внутренней логикой: регистровую и комбинационную. Такими свойствами обладают, например, ПЛИС MACH 215, семейства MACH 3, 4 и 5, а также FPGA XC3000, XC4000 [3].
Синтез конечных автоматов класса E
Пусть A - множество всех внутренних состояний конечного автомата.
Определим множество AE, AE ![]() A, состояний автомата
класса E, то есть множество состояний, коды которых определяются входными
наборами. Пусть, как и прежде, конечный автомат задан таблицей переходов,
столбцы которой имеют обозначения am, as,
X(am,as) и Y(am,as). Обозначим
через U(ai) множество всех условий переходов в состояние
ai, ai € A:
A, состояний автомата
класса E, то есть множество состояний, коды которых определяются входными
наборами. Пусть, как и прежде, конечный автомат задан таблицей переходов,
столбцы которой имеют обозначения am, as,
X(am,as) и Y(am,as). Обозначим
через U(ai) множество всех условий переходов в состояние
ai, ai € A:
U(ai) = {X(am,ai) | am € B(ai)}, (1)
где B(ai) - множество состояний, переходы из которых оканчиваются в состоянии ai. Обычно при реализации конечных автоматов на ПЛИС условие X(am,as) перехода автомата из состояния am в состояние as представляет собой некоторую элементарную конъюнкцию входных переменных. Однако в общем случае в качестве условия X(am,as) может выступать любая логическая функция, единичное значение которой вызывает переход автомата из состояния am в состояние as.
Состояние ai, ai € A, является состоянием автомата класса E, то есть ai € AE, если выполняются условия:
|U(ai)| = 1, (2)
и
U(ai)U(aj) =
(3)
при i ![]() j для всех aj € A.
j для всех aj € A.
Выполнение (2) обеспечивает осуществление всех переходов в состояние ai по одному и тому же условию перехода (то есть состояние ai имеет только один код), а выполнение (3) обеспечивает то, что условия переходов в состояние ai не вызывают переходов в другие состояния автомата (то есть состояния ai и aj имеют различные коды).
Условия (2) выполняются путём расщепления состояний. Пусть, например, для некоторого состояния ai, ai € A, имеет место |U(ai)| = H > 1. Можно расщепить состояние ai на состояния ai1,...,aiH таким образом, чтобы переходы в каждое состояние aih определялись только одним условием переходов, то есть выполнялось |U(aih)| = 1, h = ¯1,H. Теперь вместо состояния ai имеем H состояний, для которых выполняются условия (2). Выполнение условий (3) осуществляется путём введения дополнительных переменных обратных связей и соответствующих им элементов памяти для различия кодов внутренних состояний автомата.
Условия (2) и (3) являются необходимыми, но не достаточными для построения конечного автомата класса E. Дело в том, что для детерминированности поведения конечного автомата все коды его внутренних состояний должны быть взаимно ортогональны. Однако однозначное соответствие различных входных наборов различным внутренним состояниям конечного автомата, то есть выполнение условия (3), ещё не обеспечивает ортогональность кодов. Для сравнения, при синтезе автоматов классов А и В различные выходные наборы всегда ортогональны, так как это двоичные наборы. Входные же наборы представляют собой троичные векторы, причём доопределение безразличных значений входных переменных в общем случае не допустимо. Поэтому обязательным этапом синтеза конечных автоматов класса E является обеспечение ортогональности наборов входных переменных путём их доопределения с помощью дополнительных внутренних переменных.
Суть метода синтеза конечного автомата класса E заключается в расщеплении всех состояний, для которых не выполняются условия (2), и введении внутренних переменных для обеспечения ортогональности кодов внутренних состояний. Пусть P(ai) - множество переходов конечного автомата из состояния ai; C(ai) - множество переходов конечного автомата, которые оканчиваются в состоянии ai, ai € A; X(ai) - некоторое условие перехода в состояние ai, X(ai) € U(ai). Тогда алгоритм синтеза конечных автоматов класса E имеет следующий вид.
Алгоритм 1
- Для каждого внутреннего состояния ai, ai € A, согласно (1) определяется множество U(ai).
- Обеспечивается выполнение условий (2). Последовательно
просматриваются состояния множества A. Если для некоторого состояния
ai, ai € A, нарушено условие (2), то выполняется
расщепление состояния ai.
Для этого вводится H = |U(ai)| новых состояний ai1,...,aiH. Каждому состоянию aih, h = ¯1,H, ставится в соответствие одно и только одно условие X(aih) множества U(ai). Для каждого состояния aih, h = ¯1,H, определяются множества P(aih) и C(aih) следующим образом: P(aih) := P(ai), а C(aih) образуется из всех переходов, которые осуществляются при выполнении условия X(aih). Полагается: A := A \ {ai} и A := A
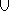 {ai1,...,aiH}.
{ai1,...,aiH}.Пункт 2 выполняется для всех состояний ai множества А.
- Вводятся дополнительные внутренние переменные для обеспечения
ортогональности кодов внутренних состояний автомата класса E. Для этого
строится троичная матрица W. Строки матрицы соответствуют внутренним
состояниям множества A, а столбцы - переменным
g1,...,gL. На пересечении строки i и столбца j
матрицы W ставится единица, если входная переменная xj входит
в условие X(ai) в прямом значении; ноль - в инверсном; и
неопределённое значение (дефис), если переменная xj не входит
в условие X(ai).
Решается следующая задача: добавить в матрицу W минимальное число столбцов, соответствующих дополнительным переменным e1,...,eR, и закодировать строки матрицы W двоичными значениями переменных e1,...,eR таким образом, чтобы все строки матрицы W были взаимно ортогональны. Алгоритм решения последней задачи приводится в [1].
- Определяются коды внутренних состояний автомата класса E. При этом код K(ai) каждого состояния ai, ai € A, будет определяться содержимым соответствующей строки матрицы W.
- Строится структурная таблица переходов конечного автомата, составляются логические уравнения функций переходов и выходов.
- Конец.
Пример 1. В качестве примера рассмотрим синтез автомата Мили класса E, таблица переходов которого представлена в табл. 1. Отметим, что поскольку |A| = 5, то при синтезе автомата Мили класса A потребуется не менее трёх элементов памяти для хранения кодов внутренних состояний. Множества U(ai), ai € A, сформированные в результате выполнения пункта 1, приведены в табл. 2. Поскольку для состояний a4 и a5 нарушены условия (2), то согласно пункту 2 выполняется их расщепление, причём состояние a4 расщепляется на два состояния, состояние a5 - на три. Построенная в пункте 3 матрица W показана в табл. 3 (первые четыре столбца). Для обеспечения ортогональности кодов внутренних состояний конечного автомата введены две дополнительные переменные e1 и e2, а также выполнено кодирование строк таблицы W (пятый и шестой столбец табл. 3). В результате определены следующие коды внутренних состояний:
K(a1) = ¯g4·¯e1·¯e2;
K(a2) = g1·¯e1·e2;
K(a3) = ¯g1·¯e1·e2;
K(a41) = g1·¯g2·e1·¯e2;
K(a4²) = g3·e1·e2;
K(a51) = g1·g1·e1·¯e2;
K(a5²) = ¯g3·e1·e2;
K(a5³) = g4·¯e1·¯e2.
Таблица 1. Исходная таблица переходов автомата Мили
| am | X(amas) | as | Y(amas) |
| a1 | x1 ¯x1 |
a2 a3 |
y3,y4 y3,y4 |
| a2 | x1
x2 x1 ¯x2 ¯x1 |
a5 a4 a3 |
y4 y3 – |
| a3 | x3 ¯x3 |
a4 a5 |
y3 y4 |
| a4 | x4 ¯x4 |
a5 a1 |
y2 – |
| a5 | x4 ¯x4 |
a5 a1 |
y1 – |
Таблица 2. Множества U(am)
| am | U(am) |
| a1 | ¯x4 |
| a2 | x1 |
| a3 | ¯x1 |
| a4 | x1 ¯x2; x3 |
| a5 | x1 x2; x3; x4 |
Таблица 3. Матрица W
| g1 | g2 | g3 | g4 | e1 | e2 | |
| a1 | - | - | - | 0 | 0 | 0 |
| a2 | 1 | - | - | - | 0 | 1 |
| a3 | 0 | - | - | - | 0 | 1 |
| a41 | 1 | 0 | - | - | 1 | 0 |
| a4² | - | - | 1 | - | 1 | 1 |
| a51 | 1 | 1 | - | - | 1 | 0 |
| a5² | - | - | 0 | - | 1 | 1 |
| a5³ | - | - | - | 1 | 0 | 0 |
Структурная таблица переходов представлена в табл. 4, на основании которой составляются следующие логические уравнения функций переходов и выходов:
d1 = g1·e1·e2·x1·x2 + g1·e1·e2·x1·x2 + g1·e1·e2;
d2 = ¯g4·¯e1·¯e2 + g1·¯e1·e2·¯x1 + ¯g1·¯e1·e2;
y1 = g1·g2·e1·¯e2·x4 + ¯g3·e1·e2·x4 + g4·¯e1·¯e2·x4;
y2 = g1·¯g2·e1·¯e2¯x4 + g3·e1·e2·x4;
y3 = ¯g4·¯e1·¯e2 + g1·e1·e2·x1·¯x2 + ¯g1·¯e1·e2·x3;
y4 = ¯g4·¯e1·¯e2 + g1·¯e1·e2·x1·x2 + ¯g1·¯e1·e2·¯x3.
Таблица 4. Структурная таблица переходов автомата класса E
| am | K(am) | X(am,as) | as | K(as) | Y(am,as) | D(am,as) |
| a1 | ¯g4·¯e1·¯e2 | x1 ¯x1 |
a2 a3 |
g1·¯e1·e2 ¯g1·¯e1·e2 |
y3,y4 y3,y4 |
d2 d2 |
| a2 | g1·¯e1·e2 | x1
x2 x1 ¯x2 ¯x1 |
a51 a41 a3 |
g1·g2·e1·¯e2 g1·¯g2·e1·¯e2 ¯g1·¯e1·e2 |
y4 y3 – |
d1 d1 d2 |
| a3 | ¯g1·¯e1·e2 | x3 ¯x3 |
a4² a5² |
g3·e1·e2 |
y3 y4 |
d1,d2 d1,d2 |
| a41 | g1·¯g2·e1·¯e2 | x4 ¯x4 |
a5³ a1 |
g4·¯e1·¯e2 ¯g4·¯e1·¯e2 |
y2 – |
- - |
| a4² | g3·e1·e2 | x4 ¯x4 |
a5³ a1 |
g4·¯e1·¯e2 ¯g4·¯e1·¯e2 |
y2 – |
- - |
| a51 | g1·g2·e1·¯e2 | x4 ¯x4 |
a5³ a1 |
g4·¯e1·¯e2 ¯g4·¯e1·¯e2 |
y1 – |
- - |
| a5² | ¯g3·e1·e2 | x4 ¯x4 |
a5³ a1 |
g4·¯e1·¯e2 ¯g4·¯e1·¯e2 |
y1 – |
- - |
| a5³ | g4·¯e1·¯e2 | x4 ¯x4 |
a5³ a1 |
g4·¯e1·¯e2 ¯g4·¯e1·¯e2 |
y1 – |
- - |
Окончательная реализация конечного автомата класса E показана на рис. 2.
Рисунок 2. Реализация на ПЛИС автомата класса E
Отметим, что в данном примере при синтезе автомата класса E, по сравнению с автоматом класса A, удалось на единицу сократить число макроячеек ПЛИС, необходимых для построения памяти конечного автомата.
Синтез конечных автоматов класса F
Существенное отличие автомата класса F от автомата класса E заключается в том, что выходные функции автомата класса F непосредственно не зависят от входных переменных. Это позволяет для построения конечных автоматов класса F использовать ПЛИС, входные буферы которых имеют только одну регистровую связь с комбинационной частью ПЛИС, например, SPLD PLS30S16; CPLD семейств MACH 1 и 2, MAX 7000, MAX 9000, FLEX [3]. Таким образом, в общем случае автоматы класса F, по сравнению с автоматами класса E, могут быть реализованы на более широком разнообразии ПЛИС. Следует однако отметить, что в некоторых случаях входные переменные могут являться аргументами дополнительных функций возбуждения элементов памяти, вводимых для различия кодов внутренних состояний автомата класса F.
Для синтеза автомата класса F без всяких изменений может быть применён алгоритм 1.
Программная реализация методов синтеза автоматов классов E и F
Рассмотренные методы синтеза конечных автоматов классов E и F реализованы программно в пакете ZUBR, при этом производится следующая последовательность действий.
- Выполняется минимизация внутренних состояний исходного конечного автомата одним из известных методов.
- Если необходимо синтезировать автомат класса F, то выполняется алгоритм 2 работы [1] расщепления внутренних состояний для приведения автомата типа Мили к эквивалентному автомату типа Мура.
- Выполняется алгоритм 1 синтеза автоматов класса E или F.
- Строится система булевых функций, соответствующая комбинационной части конечного автомата.
- Построенная в пункте 4 система булевых функций реализуется на выбранной ПЛИС одним из методов синтеза комбинационных схем.
Программа ZUBR позволяет пользователю задавать следующие режимы и параметры синтеза:
- разрешать/запрещать минимизацию внутренних состояний исходного конечного автомата;
- задавать параметры ПЛИС или указывать семейство ПЛИС из имеющегося списка;
- выбирать метод синтеза комбинационной схемы (одноуровневой, двухуровневой или многоуровневой);
- задавать параметры метода синтеза комбинационной схемы.
Дальнейшее проектирование конечного автомата может выполняться с помощью индустриального пакета. Для этого программа ZUBR позволяет представлять результаты синтеза на следующих языках проектирования: VHDL, Verilog, AHDL, Abel и других.
Результаты экспериментальных исследований методов синтеза автоматов классов E и F
Для проверки эффективности предложенных методов в качестве исходных данных использовались эталонные примеры конечных автоматов, разработанные в центре MCNC (Microelectronics Center of North Carolina) [4]. В качестве исследуемого метода синтеза рассматривался только метод синтеза конечных автоматов класса E, поскольку большинство эталонных примеров являются автоматами типа Мили. Метод синтеза автоматов класса E сравнивался с традиционными методами синтеза конечных автоматов пакета MAX+PLUSII для семейства FLEX 10K фирмы Altera и пакета Webpack для семейства VIRTEX2 фирмы Xilinx.
Результаты сравнения приведены в табл. 5 и 6, где Name - имя эталонного примера; L, N, M и P - число входов, выходов, внутренних состояний и переходов конечного автомата, соответственно; C1 - число используемых макроячеек ПЛИС при синтезе конечного автомата с помощью метода синтеза пакета MAX+PLUSII для семейства FLEX 10K; C2 - число используемых макроячеек ПЛИС семейства FLEX 10K при синтезе конечного автомата класса F с помощью рассматриваемого метода синтеза; C1/C2 - отношение C1 к C2; D1 - временная задержка, измеряемая в наносекундах, при синтезе конечного автомата с помощью метода синтеза пакета MAX+PLUSII для семейства FLEX 10K; D2 - временная задержка, измеряемая в наносекундах, при реализации конечного автомата класса F на ПЛИС семейства FLEX 10K с помощью рассматриваемого метода синтеза; D1/D2 - отношение D1 к D2; C3, C4, D3 и D4 - аналогичные параметры, но в отношении ПЛИС семейства VIRTEX2.
Таблица 5. Сравнение метода синтеза автоматов классов E и F с методом, реализованным в пакете MAX+PLUSII для семейства FLEX 10K
| Name | L | N | M | P | C1 | C2 | C1/C2 | D1 | D2 | D1/D2 |
| beecount | 3 | 4 | 7 | 28 | 37 | 10 | 3,7 | 23 | 14,1 | 1,63 |
| dk15 | 3 | 5 | 4 | 32 | 49 | 24 | 2,04 | 23,1 | 15,9 | 1,45 |
| ex3 | 2 | 2 | 10 | 36 | 22 | 10 | 2,2 | 16,4 | 18,2 | 0,90 |
| ex5 | 2 | 2 | 9 | 32 | 23 | 6 | 3,83 | 17,7 | 13,5 | 1,31 |
| ex7 | 2 | 2 | 10 | 36 | 20 | 4 | 5,0 | 18,5 | 11,5 | 1,61 |
| keyb | 7 | 2 | 19 | 170 | 102 | 83 | 1,23 | 31,3 | 28,6 | 1,09 |
| lion | 2 | 1 | 4 | 11 | 10 | 3 | 3,33 | 16,4 | 10,7 | 1,53 |
| lion9 | 2 | 1 | 9 | 25 | 23 | 3 | 7,67 | 18,2 | 11,5 | 1,58 |
| mc | 3 | 5 | 4 | 10 | 14 | 8 | 1,75 | 15,9 | 12,8 | 1,24 |
| s27 | 4 | 1 | 6 | 34 | 40 | 20 | 2,0 | 27 | 19,3 | 1,40 |
| shiftreg | 1 | 1 | 8 | 16 | 10 | 3 | 3,33 | 17,2 | 10,2 | 1,69 |
| tav | 4 | 4 | 4 | 49 | 42 | 9 | 4,67 | 22,3 | 13,2 | 1,69 |
| train11 | 2 | 1 | 11 | 25 | 24 | 3 | 8,0 | 18,6 | 10,7 | 1,74 |
| train4 | 2 | 1 | 4 | 14 | 5 | 3 | 2,0 | 12,8 | 10,7 | 1,20 |
| 50,75 | 20,06 | |||||||||
| mid | 3,63 | 1,43 |
Анализ табл. 5 показывает, что для приведённых примеров применение метода синтеза автоматов класса E, по сравнению с традиционным методом синтеза, реализованном в пакете MAX+PLUSII, позволяет снизить число используемых макроячеек ПЛИС семейства FLEX 10K, в среднем, в 3,63 раза (а для отдельных примеров - в 8 раз), при этом быстродействие конечных автоматов повышается, в среднем, в 1,43 раза (для отдельных примеров - в 1,74 раза).
Таблица 6. Сравнение метода синтеза автоматов классов E и F с методом, реализованным в пакете WebPack для семейства VIRTEX2
| Name | L | N | M | P | C1 | C2 | C1/C2 | D1 | D2 | D1/D2 |
| beecount | 3 | 4 | 7 | 28 | 31 | 8 | 3,88 | 8,57 | 6,03 | 1,42 |
| dk15 | 3 | 5 | 4 | 32 | 40 | 21 | 1,9 | 7,95 | 6,47 | 1,23 |
| ex3 | 2 | 2 | 10 | 36 | 19 | 11 | 1,73 | 7,65 | 6,47 | 1,18 |
| ex5 | 2 | 2 | 9 | 32 | 17 | 4 | 4,25 | 8,04 | 6,03 | 1,33 |
| ex7 | 2 | 2 | 10 | 36 | 17 | 3 | 5,67 | 7,20 | 5,58 | 1,29 |
| keyb | 7 | 2 | 19 | 170 | 99 | 81 | 1,22 | 10,61 | 7,82 | 1,36 |
| lion | 2 | 1 | 4 | 11 | 8 | 3 | 2,67 | 7,61 | 5,58 | 1,36 |
| lion9 | 2 | 1 | 9 | 25 | 26 | 3 | 8,67 | 7,51 | 5,58 | 1,35 |
| mc | 3 | 5 | 4 | 10 | 12 | 6 | 2,0 | 7,94 | 5,93 | 1,34 |
| s27 | 4 | 1 | 6 | 34 | 26 | 19 | 1,37 | 7,66 | 6,47 | 1,18 |
| shiftreg | 1 | 1 | 8 | 16 | 9 | 3 | 3,0 | 6,25 | 5,13 | 1,22 |
| tav | 4 | 4 | 4 | 49 | 9 | 8 | 1,13 | 7,71 | 6,03 | 1,28 |
| train11 | 2 | 1 | 11 | 25 | 27 | 3 | 9,0 | 7,63 | 5,58 | 1,37 |
| train4 | 2 | 1 | 4 | 14 | 6 | 3 | 2,0 | 6,53 | 5,58 | 1,17 |
| 48,49 | 18,08 | |||||||||
| mid | 3,46 | 1,29 |
Анализ табл. 6 показывает, что для приведённых примеров применение метода синтеза автоматов класса E, по сравнению с традиционным методом синтеза, реализованном в пакете WebPack, позволяет снизить число используемых макроячеек ПЛИС семейства VERTEX2, в среднем, в 3,46 раза (а для отдельных примеров - в 9 раз), при этом быстродействие конечных автоматов повышается, в среднем, в 1,29 раза (для отдельных примеров - в 1,42 раза).
Выводы
- Методы синтеза конечных автоматов классов E и F позволяют значительно снизить стоимость реализации и одновременно повысить быстродействие реализуемого конечного автомата.
- Снижение стоимости реализации автоматов классов E и F, по сравнению с традиционными автоматами классов A и B, осуществляется за счёт упрощения комбинационной части автомата, поскольку значительно упрощаются функции переходов, а также уменьшается число макроячеек ПЛИС для реализации памяти автомата, так как в качестве элементов памяти используются триггеры входных буферов.
- Снижению стоимости реализации автоматов классов E и F также способствует то, что в качестве кодов внутренних состояний для этих автоматов выступают элементарные конъюнкции, а не полные конъюнкции, как в традиционных моделях автоматов классов A и B.
- Повышение быстродействия автоматов классов E и F, по сравнению с традиционными автоматами классов A и B, обусловлено тем, что для этих автоматов реализуются преимущественно выходные функции, которые, как правило, значительно проще функций возбуждения элементов памяти.
- Для реализации автоматов класса F ПЛИС должны допускать буферизацию в регистрах (триггерах) значений входных переменных; для реализации автоматов класса E входные буферы ПЛИС должны иметь две связи, регистровую (буферизированную) и комбинационную (прямую), с внутренней логикой ПЛИС.
- В некоторых случаях для реализации конечных автоматов класса F также необходимо, чтобы входные буферы ПЛИС имели две связи (буферизированную и прямую) с внутренней логикой, поскольку функции возбуждения дополнительных элементов памяти могут непосредственно зависеть от входных переменных.
- Метод синтеза автоматов классов E и F не зависит от параметров ПЛИС, поэтому его можно применять для любых типов ПЛИС: основанных на концепции двух программируемых матриц или на архитектуре FPGA.
- Эффективность метода синтеза автоматов классов E и F позволяет рекомендовать разработчикам архитектур ПЛИС предусматривать возможность буферизации входных переменных, причём входные буферы должны иметь две связи с внутренней логикой ПЛИС: буферизированную (регистровую) и прямую (комбинационную).
Литература