![]() ,
,
(1)
Кулаков Николай, Подоляко Сергей
Оценка инвестиционных проектов
Источник:
http://www.cfin.ru/
Переход к
библиотеке
Для сравнения альтернативных инвестиционных проектов в теории и на практике широко используются дисконтированные критерии оценки эффективности, как-то: чистая приведенная стоимость (net present value) NPV и внутренняя ставка дохода (internal rate of return) IRR. Эти два критерия взаимно дополняют друг друга: внутренняя ставка дохода показывает доходность проекта, а чистая приведенная стоимость – размер дохода с учетом реальной стоимости денег.
Согласно [1] чистая приведенная стоимость NPV получается при дисконтировании финансовых потоков и определяет стоимость будущей прибыли проекта в настоящий момент времени для случая совершенного рынка капитала.
|
|
(1) |
где N – продолжительность проекта, выраженная в числе
шагов расчетного периода, например в годах или месяцах, ![]() i,
Zi - доходы и затраты
проекта на i шаге расчетного периода, r
– ставка дисконта.
i,
Zi - доходы и затраты
проекта на i шаге расчетного периода, r
– ставка дисконта.
Внутренняя норма дохода IRR определяется как ставка дисконта, при которой чистая приведенная стоимость равна нулю, т.е.:
|
|
(2) |
Согласно современным представлениям, внутренняя норма дохода определена только для стандартных («типичных») финансовых потоков [1, 2], т.е. таких потоков, при которых уравнение (2) имеет одно решение на экономически обоснованном интервале задания IRR.
Воспользуемся примером из [1] для пояснения понятия стандартный финансовый поток. В Таблице 1 представлены денежные потоки по годам для двух проектов, у которых на первых шагах расчетного периода осуществляются только затраты (отрицательные значения), а на последующих шагах получаются доходы (положительные значения).
Таблица 1
|
|
Денежные потоки по годам | |||||
|
0 |
1 |
2 |
3 |
4 |
5 | |
|
Проект 1 |
-60 |
11 |
15 |
18 |
18 |
18 |
|
Проект 2 |
-45 |
11 |
11 |
15 |
14 |
14 |
Зависимость NPV от ставки дисконта для этих проектов представлена на Рис.1. Как видно, в обоих случаях кривые лишь один раз пересекают ось абсцисс, и, поэтому для Проекта 1 IRR = 10%, а для Проекта 2 – 13%.
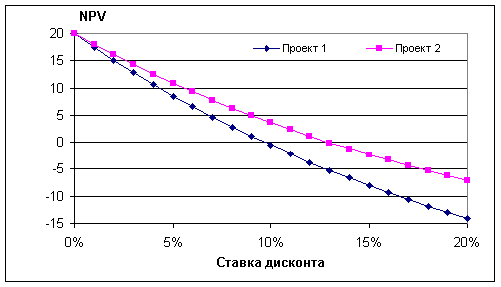
Рис. 1. Зависимость чистой приведенной стоимости от ставки
дисконта
в случае стандартного финансового потока.
В случае проектов с нестандартными («нетипичными») финансовыми потоками внутренняя ставка дохода может иметь либо несколько значений, либо вообще не определена. Более того, метод оценки таких проектов на основе IRR может противоречить оценке на основе NPV [3]. По этой причине некоторые авторы [4 5] вообще считают IRR не пригодной для оценки инвестиционных проектов..
На практике встречаются проекты, когда затраты могут осуществляться не только в начале, но и в середине или в конце расчетного периода. При этом зависимость NPV(r) отличается от изображенной на Рис.1. В качестве примера рассмотрим Проект 3 из Таблицы 2 со следующим распределением денежных потоков.
Таблица 2
|
|
Денежные потоки по годам | |||
|
0 |
1 |
2 |
3 | |
|
Проект 3 |
-10 |
60 |
-110 |
62 |
|
Проект 3а |
-10 |
59,8 |
-110 |
60,8 |
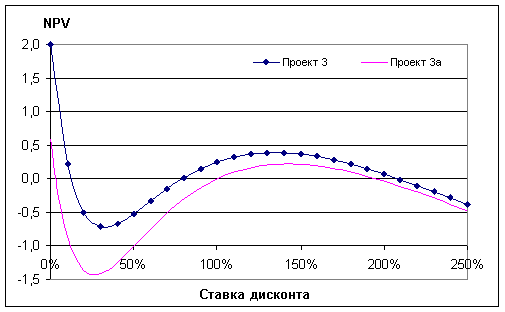
Рис. 2. Зависимость NPV от ставки дисконта в
случае
нестандартного финансового потока.
Кривая зависимости чистой приведенной стоимости от ставки дисконта показана на Рис. 2 (верхняя кривая). Как видно, кривая несколько раз (3 раза) пересекает ось абсцисс. Данный пример характеризуется нестандартным («нетипичным») финансовым потоком. Здесь NPV принимает нулевое значение при ставке дисконта: 12%, 80% и 205%.
Для стандартных потоков с некоторыми допущениями [1] IRR рассматривают как максимальную ставку, под которую можно брать кредит для реализации проекта, не превращая его в неэффективный. Посмотрим, как изменится кривая NPV в случае, если для финансирования Проекта 3 будет использован кредит. При этом условия кредитования таковы: ставка 2%, а проценты выплачиваются в конце каждого шага расчетного периода. Денежный поток для рассматриваемого примера представлен в Таблице 2 Проектом 3а, а нижняя кривая на Рис. 2 показывает зависимость NPV от ставки дисконта. Как видно, теперь NPV хотя также трижды принимает нулевое значение, но уже при значениях ставки дисконта 3%, 100% и 200
Рассмотрим пример из [1], представленный в Таблице 3. Здесь приведены два денежных потока с практической точки зрения одинаковые. Разница в инвестициях на шаге «0» составляет 0,2%, а в поступлениях на шаге «3» и того меньше – 0,1%.
Таблица 3
|
|
Денежные потоки по годам |
Прибыль проекта | |||
|
0 |
1 |
2 |
3 | ||
|
Проект A |
-1000 |
3700 |
-4540 |
1848 |
8 |
|
Проект B |
-998 |
3700 |
-4540 |
1846 |
8 |
На Рис.3. представлены зависимости NPV проектов от величины ставки дисконта.
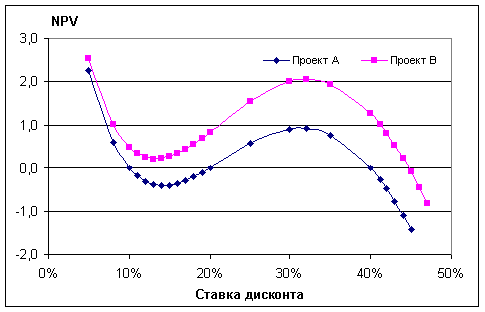
Рис. 3. Зависимость NPV от ставки дисконта.
Как видно из вышеприведённого примера, при небольшом изменении значений финансовых потоков проекта и чистой приведённой стоимости, мы формально получили иное «качество» проекта. Для Проекта А существуют три значения IRR (10%, 20% и 40%). В случае же Проекта В имеем одно значение IRR (45%). Нарушается одно из основных свойств IRR, как критерия эффективности, – непрерывность [1], когда небольшие изменения параметров не должны существенно влиять на результат.
Анализу внутренней нормы доходности в случае «нетипичных» проектов посвящено много работ [2], некоторые авторы, например, Крушвиц [4] вообще считают IRR не пригодной для оценки инвестиционных проектов. С другой стороны, из-за легкости понимания и наглядности IRR как меры доходности, много усилий было потрачено на разработку альтернативных методов оценки проектов на основе нормы дохода. Однако, все существующие методы ранжирования проектов на основе нормы дохода, оказываются не полностью совместимыми с методом NPV [5,6]. Поэтому метод на основе чистой приведенной стоимости считают предпочтительнее метода IRR [3] и рекомендуют ему следовать при оценке эффективности проектов.
В работе [7] мы определили собственную доходность проекта , которой не свойственны недостатки IRR и предложили метод ее расчета. Разберемся в чем различие нового критерия и IRR.
Определим доходность проекта как предельную процентную ставку на
вложенные средства [7]. Будем рассматривать непрерывное наращение
вложенных средств, применяя особый вид процентной ставки ![]() , которую
обычно называют силой роста [8]. Сила роста характеризует
относительный прирост наращенной суммы за бесконечно малый
промежуток времени. Тогда инвестиция Z0,
произведенная в момент
, которую
обычно называют силой роста [8]. Сила роста характеризует
относительный прирост наращенной суммы за бесконечно малый
промежуток времени. Тогда инвестиция Z0,
произведенная в момент ![]() , будет увеличиваться со
временем как
, будет увеличиваться со
временем как
|
|
(5) |
значок ~ обозначает наращенное значение. Удобство использования непрерывной ставки в том, что дальнейшее наращение уже наращенной инвестиции эквивалентно увеличению срока наращения первоначальной инвестиции, а именно:
|
|
(6) |
Если теперь, в момент ![]() доход от инвестиции
составит
доход от инвестиции
составит ![]() ,
то доходность P операции как предельная сила
роста определяется из условия:
,
то доходность P операции как предельная сила
роста определяется из условия:
|
|
(7) |
Используя метод наращения для денежного потока, определим доходность проекта в самом общем случае. Пусть денежный поток имеет вид:
![]() , где Фn =
Ф(tn) =
, где Фn =
Ф(tn) = ![]() (tn) –
Z(tn) .
(tn) –
Z(tn) .
Определим изменение наращенного денежного потока во времени при
постоянной силе ![]() . Наращение потока будем осуществлять
последовательно от момента tn
до tn+1, проходя весь расчетный интервал по
n от 0 до N. Пусть первое
ненулевое значение потока Ф0 возникло в момент t0.
Очевидно, что наращенный поток
. Наращение потока будем осуществлять
последовательно от момента tn
до tn+1, проходя весь расчетный интервал по
n от 0 до N. Пусть первое
ненулевое значение потока Ф0 возникло в момент t0.
Очевидно, что наращенный поток ![]() . В момент t1 суммарный
наращенный поток определим следующим правилом:
. В момент t1 суммарный
наращенный поток определим следующим правилом:
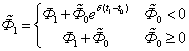
Аналогично в момент t2 наращенный поток будет равен:
|
|
(8) |
Отметим, что очередному наращению подлежат только отрицательные
значения. Поясним смысл этого ограничения. Пусть в момент t0
вы положили (инвестировали) в банк сумму Ф0 под
проценты, начисляемые по непрерывной ставке ![]() на условиях вклада до
востребования (считаем, что каждый день на остаток начисляются
сложные проценты). Затем в момент t1 вы пришли и сняли сумму
Ф1. Если вы сняли не всю наращенную к этому моменту времени
сумму
на условиях вклада до
востребования (считаем, что каждый день на остаток начисляются
сложные проценты). Затем в момент t1 вы пришли и сняли сумму
Ф1. Если вы сняли не всю наращенную к этому моменту времени
сумму ![]() , то
на оставшиеся деньги будут также начисляться проценты. Если же вы
снимете всю наращенную сумму
, то
на оставшиеся деньги будут также начисляться проценты. Если же вы
снимете всю наращенную сумму ![]() , то ваш счет в банке
обнулится и сумма вклада не будет меняться со временем, т.к.
на нулевую сумму банк не будет начислять проценты. Если же вы
снимите сумму, превышающую ваш имеющийся вклад (так называемый
овердрафт)
, то ваш счет в банке
обнулится и сумма вклада не будет меняться со временем, т.к.
на нулевую сумму банк не будет начислять проценты. Если же вы
снимите сумму, превышающую ваш имеющийся вклад (так называемый
овердрафт) ![]() , то скорее всего уже банк будет начислять вам проценты на
возникший заем.
, то скорее всего уже банк будет начислять вам проценты на
возникший заем.
Таким образом, общее правило для расчета наращенного потока к моменту tn имеет вид:
|
|
(9) |
Продолжая последовательно наращивать отрицательные значения
наращенного потока согласно (9) к моменту tN
будем иметь наращенный поток ![]() . Предельная сила роста
определяется из условия, что наращенный поток в момент
. Предельная сила роста
определяется из условия, что наращенный поток в момент ![]() равен
0. Имеем:
равен
0. Имеем:
|
|
(10) |
Мы утверждаем, что предельная сила роста ![]() , определяемая в
результате решения рекуррентной системы уравнений (9,10) и есть
доходность проекта как такового. Мы назвали ее собственной
доходностью. Собственная доходность как критерий,
основанный на норме дохода, применим для проектов с любыми
финансовыми потоками! В случае проектов с «типичным»
финансовым потоком, собственная доходность эквивалентна
внутренней норме дохода. Докажем последнее утверждение.
, определяемая в
результате решения рекуррентной системы уравнений (9,10) и есть
доходность проекта как такового. Мы назвали ее собственной
доходностью. Собственная доходность как критерий,
основанный на норме дохода, применим для проектов с любыми
финансовыми потоками! В случае проектов с «типичным»
финансовым потоком, собственная доходность эквивалентна
внутренней норме дохода. Докажем последнее утверждение.
Определением «типичного» потока в принятом нами изложении будет условие:
|
|
(11) |
тогда последовательно применяя формулу (9) от N до 0 получим формулу для расчета наращенной суммы «типичного» денежного потока:
|
|
(12) |
Эта формула означает, что все слагаемые потока наращиваются от момента появления до конца проекта. Приравняв (12) к нулю, получим уравнение для расчета IRR, а именно:
|
|
(13) |
Чтобы доказать это, умножим (12) на ![]() , что равносильно
дисконтированию всех слагаемых потока к началу проекта. В результате
получим уравнение для расчета NPV при
непрерывной ставке дисконта, а именно:
, что равносильно
дисконтированию всех слагаемых потока к началу проекта. В результате
получим уравнение для расчета NPV при
непрерывной ставке дисконта, а именно:
![]() .
.
Приравняв его к нулю, получим уравнение для расчета IRR, что и требовалось доказать.
Определим теперь собственную доходность рассмотренных выше проектов. Проекты 1 и 2, потоки которых приведены в Таблице 1, имеют соответственно доходность 10% и 13%, которые совпадают со ставками IRR этих проектов (см. Рис. 1). Собственная доходность Проекта 3 из Таблицы 2 равна 2,85%, а проекта 3а – 0,85%. Как видим, доходности их отличаются ровно на ставку по кредиту, равную 2%, что очень даже логично. Нет никакой путаницы с выбором одной из трех ставок IRR, тем более что ни одна из этих ставок не имеет ничего общего с доходностью проекта. Наконец, собственная доходность Проектов А и В из Таблицы 3 равна 0,2814% и 0,2818% соответственно. Относительная разница в значениях всего 0,14%. Это подтверждает очевидный, судя по денежным потокам, факт, что проекты практически одинаковы. При этом к собственной доходности в отличие от IRR применимо свойство непрерывности.
Можно показать, что.![]() , где
, где ![]() - монотонно убывающая функция, а
следовательно собственная доходность в отличие от IRR определена для проектов с любыми
денежными потоками, если выполняется следующее условие
- монотонно убывающая функция, а
следовательно собственная доходность в отличие от IRR определена для проектов с любыми
денежными потоками, если выполняется следующее условие![]() и рассматривается
диапазон
и рассматривается
диапазон ![]() .
.
Таким образом, собственная доходность проекта есть предельная сила роста или процентная ставка, удовлетворяющая уравнениям (9) и (10). Собственная доходность в отличие от IRR определена для проектов с любыми денежными потоками.
Рассмотрим уравнения (9) и (12) определяющие наращенную сумму
денежного потока для расчета собственной доходности и внутренней
нормы дохода. Выясним разницу между уравнениями, это позволит
понять, почему для «нетипичных» потоков всегда существует
единственно возможная сила роста ![]() , но не всегда
определена IRR.
, но не всегда
определена IRR.
Таблица 4.
|
|
Денежные потоки по годам | |||
|
0 |
1 |
2 |
3 | |
|
Проект 4 |
-100 |
230 |
0 |
-150 |
Рассмотрим проект с денежным потоком, представленным в Таблице 4. Наращенная сумма потока согласно уравнению (12) определяется выражением:
|
|
(14а) |
а согласно уравнению (9) выражением:
|
|
(14б) |
График зависимости наращенной суммы потока Проекта 4 в зависимости от силы роста в обоих случаях представлены на Рис.4.
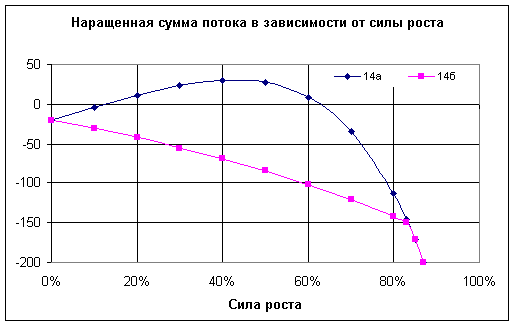
Рис. 4. Зависимость наращенной суммы потока,
рассчитанной по
формулам 14а и 14б, от силы роста
Как видно из рисунка, наращенная сумма потока при силе роста
более 83% определяется одинаково обеими формулами. Иначе обстоит
дело при силе роста меньше 83%. Так, кривая 14а дважды пересекает
ось абсцисс при значениях ![]() 13% и 63%. Что соответствует двум значениям
внутренней нормы дохода IRR. Какую же из ставок
считать доходностью проекта? С учетом выше сказанного, ни одно из
этих значений не определяет доходность данного проекта, что
подтверждает кривая 14б, которая вообще не пересекает ось абсцисс
при положительных значениях
13% и 63%. Что соответствует двум значениям
внутренней нормы дохода IRR. Какую же из ставок
считать доходностью проекта? С учетом выше сказанного, ни одно из
этих значений не определяет доходность данного проекта, что
подтверждает кривая 14б, которая вообще не пересекает ось абсцисс
при положительных значениях ![]() . Следовательно,
проект убыточен, что собственно было ясно сразу, т.к. суммарный
денежный поток без наращения отрицателен (-20). Хотя традиционный
метод оценки проекта на основе дисконтированного потока говорит об
обратном (при силе дисконта 30% NPV > 0, см. Рис. 7). Это мы обсудим ниже,
а сейчас объясним суть различия между собственной доходностью и
IRR.
. Следовательно,
проект убыточен, что собственно было ясно сразу, т.к. суммарный
денежный поток без наращения отрицателен (-20). Хотя традиционный
метод оценки проекта на основе дисконтированного потока говорит об
обратном (при силе дисконта 30% NPV > 0, см. Рис. 7). Это мы обсудим ниже,
а сейчас объясним суть различия между собственной доходностью и
IRR.
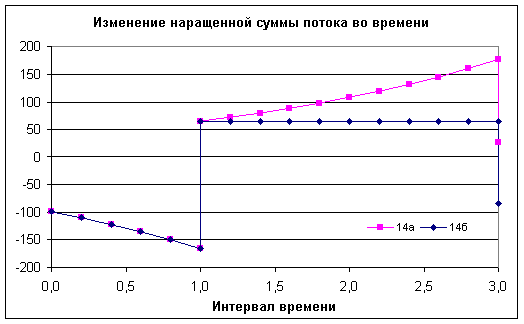
Рис.5. Зависимость наращенной суммы потока, рассчитанной
по
формулам 14а и 14б, от времени.
Рассмотрим графики на Рис.5, показывающие как изменяется
наращенная сумма потока со временем. При использовании формулы 14а
меняются (увеличиваются) как отрицательные, так и положительные
значения потока. При использовании формулы 14б наращиваются только
отрицательные значения потока, а положительные значения не меняются
со временем. В результате итоговые значения наращенного потока
к концу проекта оказываются разными по величине для формул 14а и
14б. В случае 14а из-за того, что положительные значения
потока также наращиваются по непрерывной ставке ![]() , итоговая сумма
становится положительной! Однако доходы проекта (положительный
поток) могут быть увеличены только за счет размещения их в другом
проекте, но никак не данном. Расчет внутренней нормы дохода
подразумевает, что свободные средства проекта могут быть
реинвестированы (размещены на денежном рынке) по ставке
IRR. Однако, это не верно! Во-первых:
свободные средства, возможно, могут быть размещены на депозите по
рыночной ставке Е [1] или реинвестированы по
средневзвешенной цене капитала WACC [3]. Но эти ставки меньше
IRR, иначе проект убыточен. Во-вторых:
доходность проекта становится зависимой от доходности других
проектов и операций. Какой тогда смысл во внутренней норме дохода !
, итоговая сумма
становится положительной! Однако доходы проекта (положительный
поток) могут быть увеличены только за счет размещения их в другом
проекте, но никак не данном. Расчет внутренней нормы дохода
подразумевает, что свободные средства проекта могут быть
реинвестированы (размещены на денежном рынке) по ставке
IRR. Однако, это не верно! Во-первых:
свободные средства, возможно, могут быть размещены на депозите по
рыночной ставке Е [1] или реинвестированы по
средневзвешенной цене капитала WACC [3]. Но эти ставки меньше
IRR, иначе проект убыточен. Во-вторых:
доходность проекта становится зависимой от доходности других
проектов и операций. Какой тогда смысл во внутренней норме дохода !
Таким образом, при расчете внутренней нормы дохода применяется некорректное условие, а именно: все потоки проекта могут быть размещены по ставкеIRR, что является справедливым только для «типичного» денежного потока. В случае «нетипичного» потока, это условие не всегда выполняется, т.е. не всегда доходы проекта могут быть реинвестированы в сам проект по ставке IRR. При расчете собственной доходности реинвестирование положительных наращенных потоков в проект по ставкеIRR всегда запрещено.
Анализируя различные методы оценки проектов на основе нормы дохода, всегда обращают внимание на совместимость этих методов с оценкой на основе NPV [2,6], считая последнее правило оптимальным. Напомним, в чем суть метода оценки на основе чистой приведенной стоимости [3].
Если NPV > 0, проект следует принять, если NPV < 0, проект должен быть отвергнут. Если имеются два взаимоисключающих проекта, то должен быть выбран тот, у которого положительный NPV больше.
Логика данного критерия достаточно очевидна. Нулевой NPV означает, что получаемого в ходе проекта денежного потока вполне достаточно для возмещения вложенного в проект капитала и обеспечения требуемой отдачи на этот капитал. При нулевом NPV стоимость фирмы не меняется - масштабы производства растут, но стоимость акций не меняется. Если NPV > 0, тогда проект увеличивает стоимость фирмы. Поэтому из двух проектов следует выбирать тот, который дает большую стоимость.
Важным параметром при расчете чистой приведенной стоимости является ставка дисконта. От ее величины зависит значение NPV, а, следовательно, и решение об инвестициях. Рассмотрим для примера два проекта с денежными потоками, представленными в Таблице 5.
Таблица 5
|
Проект \ Период |
1 |
2 |
3 |
|
Проект С |
-100 |
130 |
0 |
|
Проект |
-100 |
0 |
150 |
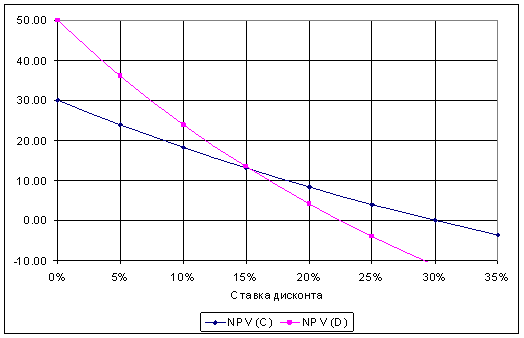
Рис. 6. Зависимость NPV от ставки дисконта.
Зависимость NPV от ставки дисконта
для обоих проектов показана на Рис. 6. Как видно из рисунка, при
r < 15% NPV
Проекта ![]() больше, следовательно, выгоднее принять этот
проект. Однако при r > 15% уже Проект C имеет больший NPV и значит,
следует принять его. При r > 23%
от Проекта
больше, следовательно, выгоднее принять этот
проект. Однако при r > 15% уже Проект C имеет больший NPV и значит,
следует принять его. При r > 23%
от Проекта ![]() вообще следует отказаться, следуя правилу NPV .
Можно сразу предположить, что следует выбирать проект с
большим NPV при более высокой ставке
дисконта. Однако, это предположение не всегда верно.
вообще следует отказаться, следуя правилу NPV .
Можно сразу предположить, что следует выбирать проект с
большим NPV при более высокой ставке
дисконта. Однако, это предположение не всегда верно.
Определению величины дисконтной ставки уделено достаточно много
внимания [3]. В основе лежит цена капитала, инвестируемого в проект.
Расчет цены капитала фирмы предполагает выделение основных его
составляющих и вычисления их цены. Результаты расчета сводятся в
единый показатель, называемый средневзвешенной ценой капитала
WACC (Weighted
Average Cost
of
Capital). Однако, выбор ставки
дисконта при расчете NPV, равной цене капитала,
справедлив для безрисковых или почти безрисковых проектов. В случае,
когда инвестиции в проект сопряжены с рисками (снижение
запланированных доходов, увеличение расходов и т.д.) в ставку
дисконта включают премию за риск. Такой подход всегда повышает
ставку дисконта, и тогда вероятнее выбор Проекта C. Не
наступление рискового случая при завершении проекта ведет к потере
прибыли, т.к. задним числом менеджер понимает, что надо было выбрать
Проект ![]() . К
тому же, расчет премии выполняется, как правило, достаточно
субъективно и поэтому высока вероятность ошибки. А в случае проектов
с «нетипичным» денежным потоком включение премии в ставку
дисконта вообще абсурд.
. К
тому же, расчет премии выполняется, как правило, достаточно
субъективно и поэтому высока вероятность ошибки. А в случае проектов
с «нетипичным» денежным потоком включение премии в ставку
дисконта вообще абсурд.
С течением времени цена капитала может меняться, и принятый при прежних условиях проект может быть отвергнут. Сделать точный прогноз цены капитала весьма не просто, а значит и значение NPV правильно оценить не всегда возможно. Поэтому очень важен «резерв безопасности проекта» [3], показателем которого является доходность. Инвесторам куда понятнее оперировать критерием доходности проекта, который никоим образом не зависит от ставки дисконта. Внутренняя норма дохода, как известно, не всегда соответствует доходности, поэтому не во всех случаях её можно использовать.
Оценим с позиций правила NPV Проект 4 из Таблицы 4. Кривая зависимости чистой приведенной стоимости от величины ставки дисконта приведена на Рис. 7. Правило NPV говорит, что при цене капитала больше 13% (например, при WACC = 20%, NPV > 0), проект следует принять. А что говорит правило IRR?
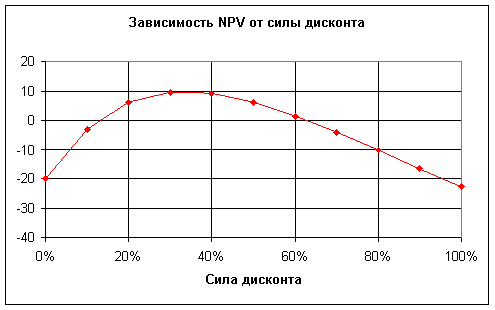
Рис.7. Зависимость чистой приведенной стоимости от силы дисконта.
У проекта два значения IRR (13% и 63%). Следуя теории [1] в качестве IRR следует принять первое значение, на это также указывает модифицированная норма дохода MIRR [3], равная 10%. Но, согласно правилу IRR проект принимается, если для всех ставок дисконтирования меньших IRR выполнено условие NPV > 0. Поэтому согласно правилу IRR Проект 4 должен быть отвергнут. Между правилами возникает противоречие. Чистый приведенный поток положителен при ставках дисконта больших IRR, а не меньших. Ничего не меняет замена IRR модифицированной нормой дохода, между методами оценки, основанными на MIRR и NPV такое же противоречие. По этой причине многие экономисты для оценки эффективности инвестиций и принятия решения советуют использовать лишь одно правило NPV.
Однако на столько уж безупречен метод оценки на основе чистой приведенной стоимости? Ведь сальдо проекта отрицательно. Положительным приведенный поток становится только при условии размещения доходов Проекта 4 в других проектах, что в принципе возможно. Например, размещение свободных средств на депозите под проценты или покупка акций, по которым выплачиваются дивиденды. Пусть размещение средств возможно по ставке, равной средневзвешенной цене капитала WACC. Какова тогда собственная доходность P Проекта 4?
Согласно (8) и (9) результирующий наращенный поток будет равен:
![]() ,
,
здесь учтено, что положительный наращенный поток размещается на
два года по ставке, равной WACC (20%). Тогда
решая уравнение ![]() , получим P =
, получим P = ![]() пред = 25% и
собственная доходность превышает стоимость капитала.
Следовательно, Проект 4 следует принять.
пред = 25% и
собственная доходность превышает стоимость капитала.
Следовательно, Проект 4 следует принять.
Таким образом, оценка проектов с «нетипичными» финансовыми потоками на основе правила собственной доходности, эквивалентного правилу IRR, совпадает с оценкой на основе правила NPV.
В настоящей работе изложено следующее:
1. Предложен метод расчета доходности проекта как предельной силы роста наращенной суммы инвестируемых средств. Показано, что данный метод исключает неоднозначность определения доходности в случае «нетипичных» финансовых потоков.
2. Введено понятие собственной доходности проекта. Собственная доходность является в самом общем случае доходностью собственно проекта (как генератора прибыли), и в отличие от IRR не предполагает капитализацию свободных средств. Показано, что IRR является частным случаем собственной доходности и совпадает с ней при «типичных» финансовых потоках.
3. Рассмотрено правило принятия решения об инвестициях на основе собственной доходности. Данное правило эквивалентно правилу IRR , и совместимо с правилом NPV в случае любых, в том числе и «нетипичных» финансовых потоков.
Литература.
1.Виленский П.Л., Лифшиц В.Н., Смоляк С.А. Оценка эффективности инвестиционных проектов: Теория и практика. – М.: Дело, 2002.
2.Proctor, Michael D. and John R. Canada, "Past and Present Methods of Manufacturing Investment Evaluation: A Review of the Empirical and Theoretical Literature," The Engineering Economist, Fall 1992, Vol. 38, No. 1.
3.Бригхем Ю., Гапенски Л. Финансовый менеджмент: Полный курс: в 2-х т. – СПб.: Экономическая школа, 2001.
4. Крушвиц Л. Инвестиционные расчеты. – СПб.: Питер, 2001.
5.Block, Stanley "Capital Budgeting Techniques Used by Small Business Firms in the 1990s," The Engineering Economist, Summer 1997, Vol. 42, No.4.
6. Hajdasinsky, Miroslaw M. "NPV-Compatibility, Project Ranking, and Related Issues," The Engineering Economist, Summer 1997, Vol. 42, No. 4.
7. Кулаков Н.Ю., Подоляко С.В. Расчет доходности инвестиционных проектов в случае нестандартных финансовых потоков. – М.: Сборник научных трудов, РосЗИТЛП, 2004.
8.Лытнев О.Н., Основы финансового менеджмента. Курс лекций. – М.: Дело, 2001.
Переход к библиотеке