Первоисточник: http://en.wikipedia.org/wiki/Finite_state_machine
Статья посвящена конечным управляющим автоматам, их классификации. В ней рассматриваются два класса управляющих автомата: автомат Мура и автомат Мили.
Finite state machine
A finite state machine (FSM) , finite state automaton (plural: automata ) is a model of behavior composed of a finite number of states , transitions between those states, and actions.
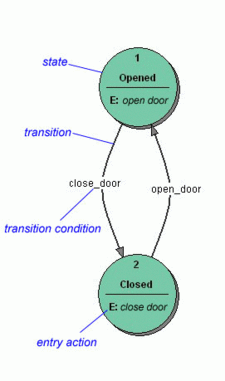
Fig.1 Finite State Machine
Concepts and vocabulary
A state stores information about the past, i.e. it reflects the input changes from the system start to the present moment. A transition indicates a state change and is described by a condition that would need to be fulfilled to enable the transition. An action is a description of an activity that is to be performed at a given moment. There are several action types:
Entry action
which is performed when entering the state
Exit action
which is performed when exiting the state
Input action
which is performed depending on present state and input conditions
Transition action
which is performed when performing a certain transition
FSM can be represented using a state diagram (or state transition diagram) as in figure 1. Besides this, several state transition table types are used. The most common representation is shown below: the combination of current state (B) and condition (Y) shows the next state (C). The complete actions information can be added only using footnotes. An FSM definition including the full actions information is possible using state tables (see also VFSM ).
State transition table |
|||
Current State/ |
State A |
State B |
State C |
Condition X |
... |
... |
... |
Condition Y |
... |
State C |
... |
Condition Z |
... |
... |
... |
In addition to their use in modeling reactive systems presented here, finite state automata are significant in many different areas, including electrical engineering , linguistics , computer science , philosophy , biology , mathematics , and logic . A complete survey of their applications is outside the scope of this article. Finite state machines are a class of automata studied in automata theory and the theory of computation . In computer science, finite state machines are widely used in modeling of application behavior, design of hardware digital systems, software engineering, compilers, network protocols, and the study of computation and languages.
Classification
There are two different groups: Acceptors/Recognizers and Transducers.
Transducers
Transducers generate output based on a given input and/or a state using actions. They are used for control applications. Here two types are distinguished:
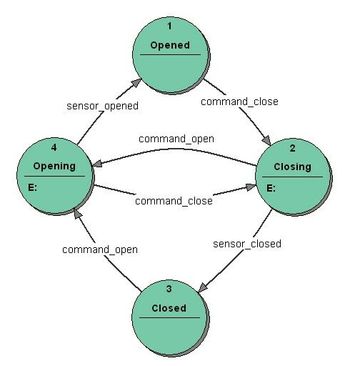
Fig. 2 Transducer FSM: Moore model example
The FSM uses only entry actions, i.e. output depends only on the state. The advantage of the Moore model is a simplification of the behaviour. The example in figure 2 shows a Moore FSM of an elevator door. The state machine recognizes two commands: "command_open" and "command_close" which trigger state changes. The entry action (E:) in state "Opening" starts a motor opening the door, the entry action in state "Closing" starts a motor in the other direction closing the door. States "Opened" and "Closed" don't perform any actions. They signal to the outside world (e.g. to other state machines) the situation: "door is open" or "door is closed".

Fig. 3 Transducer FSM: Mealy model example
The FSM uses only input actions, i.e. output depends on input and state. The use of a Mealy FSM leads often to a reduction of the number of states. The example in figure 3 shows a Mealy FSM implementing the same behaviour as in the Moore example (the behaviour depends on the implemented FSM execution model and will work e.g. for virtual FSM but not for event driven FSM ). There are two input actions (I:): "start motor to close the door if command_close arrives" and "start motor in the other direction to open the door if command_open arrives".
In practice mixed models are often used.
More details about the differences and usage of Moore and Mealy models, including an executable example, can be found in the external technical note "Moore or Mealy model?"
A further distinction is between deterministic ( DFA ) and non-deterministic ( NDFA , GNFA ) automata. In deterministic automata, for each state there is exactly one transition for each possible input. In non-deterministic automata, there can be none or more than one transition from a given state for a given possible input. This distinction is relevant in practice, but not in theory, as there exists an algorithm which can transform any NDFA into an equivalent DFA, although this transformation typically significantly increases the complexity of the automaton.
The FSM with only one state is called a combinatorial FSM and uses only input actions. This concept is useful in cases where a number of FSM are required to work together, and where it is convenient to consider a purely combinatorial part as a form of FSM to suit the design tools.