Первоисточник: http://www.chipinfo.ru/literature/chipnews/200305/3.html
В. Соловьев, А. Климович
Рассматриваются общие вопросы проектирования комбинационных схем на основе ПЛИС. Предлагается аналитический обзор наиболее известных методов синтеза комбинационных схем: традиционных и реализованных в широко используемых программных пакетах. Особое внимание при этом уделено работам зарубежных авторов, мало известным отечественным читателям. Описываются архитектурные возможности современных ПЛИС при реализации комбинационных схем. Для этого вводятся три архитектурные модели ПЛИС со структурой двух программируемых матриц: "классические" PAL, универсальные PAL и CPLD. Приводится также характеристика нового подхода к проектированию комбинационных схем на ПЛИС, который будет описан в следующих статьях данной серии.
Введение
В предыдущих статьях [2-5] рассматривались различные методы синтеза конечных автоматов на ПЛИС, важное место в которых занимает синтез комбинационной части конечного автомата, представляющей собой комбинационную схему. При разработке различных цифровых систем проектировщики часто сталкиваются с необходимостью синтеза комбинационных схем. Кроме комбинационных частей конечных автоматов, комбинационные схемы широко используются в качестве оригинальных функциональных узлов, функционирование которых не совпадает с работой стандартных функциональных узлов комбинационного типа. Поэтому мы решили включить в данную серию несколько статьей, посвящённых проблеме проектирования комбинационных схем.
Настоящая статья является вводной, в ней рассматриваются общие вопросы, касающиеся проблемы проектирования комбинационных схем на ПЛИС. В последующем предполагается опубликовать следующие статьи:
Под комбинационной схемой понимается логическая схема, значения выходных сигналов которой в каждый момент времени полностью определяются значениями сигналов на её входах. Иногда говорят, что комбинационная схема — это конечный автомат с одним состоянием или последовательностная схема без памяти. Однако методы синтеза конечных автоматов и комбинационных схем значительно различаются между собой.
Пусть комбинационная схема задана системой булевых функций (СБФ), представленных в дизъюнктивной нормальной форме (ДНФ) [1]. СБФ будем характеризовать числом N выходных функций (выходных переменных) множества Y = {y1,...,yN} и числом L аргументов функций (входных переменных) множества X = {x1,...,xL}. Кроме того, каждая функция yi характеризуется числом Q(yi) слагаемых в ДНФ функции yi, yi € Y. Если функция yi представлена кратчайшей ДНФ, содержащей минимальное число слагаемых, то значение Q(yi) совпадает с числом промежуточных шин ПЛИС, требуемых для её реализации.
Традиционные методы синтеза комбинационных схем
Методы синтеза комбинационных схем принято делить на два больших класса: двухуровневый и многоуровневый синтез.
Двухуровневый синтез предполагает прохождение сигнала со входа на выход комбинационной схемы через два уровня логических элементов, обычно это вентили И и ИЛИ, и соответствует синтезу комбинационных схем на ПЛИС со структурой двух программируемых матриц. Многоуровневый синтез обычно сводится к синтезу логической сети, узлами которой являются логические элементы, и соответствует синтезу комбинационных схем на FPGA (Field Programmable Gate Array).
Главной задачей двухуровневого синтеза является минимизация булевых функций в классе ДНФ. Первые решения этой задачи [10,17] принято считать классическими. Целью минимизации булевых функций является сокращение числа слагаемых и литералов в представлении булевых функций. Напомним, что при синтезе комбинационных схем на ПЛИС достаточно минимизировать число слагаемых булевой функции, то есть найти кратчайшую ДНФ [1].
Задаче минимизации булевых функций посвящено огромное число работ, простое перечисление которых уже представляет собой далеко не тривиальную задачу. Поэтому ограничимся указанием основных направлений данных исследований: точные алгоритмы, эвристические алгоритмы, минимизация частично определённых булевых функций, минимизация слабо определённых булевых функций, совместная минимизация СБФ и др.
Следующее направление развития двухуровневого синтеза связано с использованием концепции многозначных функций. В соответствии с этой концепцией СБФ рассматривается как одна функция с одним многозначным входом и одним многозначным выходом, а одна булева функция нескольких аргументов - как многозначная функция с бинарным выходом.
В [22] классические методы минимизации булевых функций были расширены для многозначных входов и бинарных выходов. В [21] показано, что минимизация СБФ сводится к минимизации одной бинарной функции с многозначными аргументами.
Хотя на первый взгляд это может показаться странным, но ключевой момент в развитии методов двухуровневого синтеза комбинационных схем непосредственно связан с новым подходом к синтезу конечных автоматов. В [14,15] предложено минимизацию комбинационной части конечного автомата выполнять до этапа кодирования внутренних состояний, а внутренние состояния, входные и выходные наборы представлять в символьной форме. Подобный подход получил название символьной минимизации, которая тесно связана с многозначной логической минимизацией. Таким образом, минимизация комбинационной части конечного автомата сводится к минимизации многозначной функции.
Поскольку частично определённые булевы функции можно рассматривать как многозначную функцию, а доопределение значений частично определённых булевых функций - как аналог кодирования внутренних состояний конечного автомата, то методы символьной минимизации могут также применяться и для синтеза комбинационных схем. Классические методы синтеза СБФ принято называть булевыми методами, а методы синтеза многозначных и символьных функций - алгебраическими методами синтеза комбинационных схем.
Наиболее известной программной реализацией двухуровневого синтеза комбинационных схем является программа ESPRESSO [7], разработанная в лаборатории электронных исследований Калифорнийского университета в Беркли (США). Приближенные методы многозначной минимизации реализованы в программе ESPRESSO-MV [19,20], а точные - в ESPRESSO-EXACT [20].
Целью многоуровневого синтеза является синтез комбинационной схемы в виде логической сети, удовлетворяющей заданным ограничениям. Ограничения на синтез логической сети, в основном, касаются типов логических элементов, выступающих в качестве узлов сети, их параметров и коэффициентов разветвления по входам и выходам. Главными критериями оптимизации при многоуровневом синтезе являются длина критического пути прохождения сигнала со входа на выход (время максимальной задержки) и площадь (стоимость), занимаемая логической сетью. Причём при определении площади сети часто учитывается не только площадь логических элементов, но и площадь межсоединений. Многоуровневый синтез обычно применяется при реализации комбинационных схем на заказных и полузаказных СБИС, а также на FPGA.
В основе методов многоуровневого синтеза лежат классические методы декомпозиции и факторизации булевых функций [6,8,11,18]. Классические методы были развиты в работе [12], где предложены точные и приближенные алгоритмы минимизации многовыходной логической сети при ограничениях на число уровней сети и на коэффициенты расширения выходов вентилей. Классические методы, хотя и позволяют получать точные решения, однако не пригодны для решения задач большой размерности. Поэтому для практического применения были разработаны приближенные методы многоуровневого синтеза, основанные на локальных преобразованиях логических сетей.
Следующее направление развития логических методов многоуровневого синтеза связано с широким использованием программируемых логических матриц (ПЛМ - Programmable Logic Array - PLA) для построения комбинационных схем.
Первые методы решения задач многоуровневого синтеза были основаны на дизъюнктивном разложении Шеннона. Однако ввиду своей малой эффективности, данный подход не получил широкого распространения.
Недостатком традиционных методов декомпозиции является необходимость в разбиении множества X на два непересекающихся подмножества X1 и X2. В отдельных работах предлагаются подходы, в которых допускается пересечение множеств X1 и X2. В ряде случаев это позволяет более качественно решать задачу декомпозиции с точки зрения минимизации числа входов ПЛМ нижнего уровня и числа используемых промежуточных шин ПЛМ.
Большинство современных методов многоуровневого синтеза реализовано в программе MIS [9] и её модификациях, которая была разработана в лаборатории электронных исследований Калифорнийского университета в Беркли. В программе MIS реализованы как быстрые, так и медленные алгоритмы, а также алгебраические и булевы методы, основанные на операциях деления, выделения ядра и подстановки. В подсистеме MIS-MV [13] реализованы методы многозначной минимизации многоуровневого синтеза. Ввиду широкого распространения FPGA на основе функциональных генераторов (Look-Up Table - LUT) специально была разработана программа MIS-PGA [16], ориентированная на узлы логической сети данного типа.
Возможности ПЛИС при синтезе комбинационных схем
Ограничимся рассмотрением архитектур ПЛИС, в основе структуры которых лежат две программируемые матрицы: "классических" PAL (Programmable Array Logic), универсальных PAL и CPLD (Complex Programmable Logic Device).
Возможности "классических" PAL
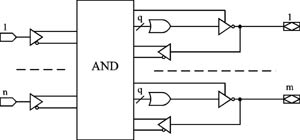
Структура "классических" PAL изображена на рис. 1. Она включает n входов, программируемую матрицу AND и m выходных макроячеек, связанных с двунаправленными выводами. Выходы матрицы AND называются промежуточными шинами или термами. Архитектура выходных макроячеек "классических" PAL достаточно проста, для комбинационных выходов она включает вентиль ИЛИ, объединяющий q промежуточных шин, выходной буфер с тремя состояниями и обратную связь со входом матрицы AND. Все входы матрицы AND являются парафазными. Для управления третьим состоянием выходного буфера служит отдельная промежуточная шина.
Рисунок 1. Обобщённая структура "классической" PAL

Рассмотрим возможности, которые предоставляет архитектура "классических" PAL при реализации СБФ. Прежде всего, поскольку все входы матрицы AND являются парафазными, отпадает необходимость специально инвертировать входные переменные. Таким образом, на промежуточных шинах можно реализовать любую конъюнкцию входных переменных и их инверсий, а также переменных обратных связей, максимальный ранг (число литералов) которой не превышает значение n+m-1 (один выход необходим для реализации функции).
Далее, с каждой выходной макроячейкой PAL связано отдельное множество промежуточных шин. Это позволяет применять раздельную минимизацию булевых функций, что значительно упрощает задачу, поскольку минимизация одной булевой функции решается намного проще и качество её решения лучше, чем совместная минимизация СБФ [1]. Кроме того, нет необходимости применять классические методы минимизации, рассчитанные на реализацию булевых функций из отдельных вентилей, а достаточно найти кратчайшую ДНФ. "Классические" PAL также позволяют программировать высокоимпедансное (третье) состояние выходного буфера, что делает возможным двунаправленный вывод использовать как вход. Кроме того, индивидуальное управление с помощью отдельного терма третьим состоянием выходного буфера позволяет двунаправленный вывод в один момент времени использовать как выход, а в другой момент - как вход или отключать от внешней шины, например, для уменьшения нагрузки.
Возможность PAL передачи значения выходного сигнала по цепи обратной связи на вход матрицы AND позволяет в одном устройстве строить многоуровневые каскадные схемы. Однако следует избегать случаев, когда значение некоторой функции является аргументом этой же функции, так как в подобной ситуации схема перестаёт быть комбинационной и переходит в класс последовательностных схем, а отсутствие в циклах элементов задержки приводит к непредсказуемости поведения схемы.
Классическая PAL допускает реализацию любой СБФ (тривиальная реализация), если выполняются условия:
N <= m;
L <= n + m – N; (1)
Q(yi) <= q; для всех yi € Y.
Первое неравенство в условии (1) накладывает ограничение на число реализуемых функций, второе - на число аргументов функций, а третье - на число слагаемых в ДНФ каждой функции.
Нарушение первых двух неравенств в (1) делает реализацию СБФ на одной классической PAL невозможной. Если в (1) для некоторой функции yi, yi О Y, нарушено третье неравенство, то прежде всего необходимо выполнить минимизацию функции yi одним из известных методов.
Возможности универсальных PAL
Обобщенная структура универсальных PAL (рис. 2) включает n входов, программируемую матрицу AND, m выходных макроячеек с одной обратной связью и m2 макроячеек с двумя обратными связями. Архитектура макроячейки с двумя обратными связями показана на рис. 3. В макроячейках с одной обратной связью отсутствует цепь от входа выходного буфера к входу матрицы AND. С каждой макроячейкой универсальных PAL связано различное число промежуточных шин, что позволяет более рационально их использовать: простые функции назначать для реализации на выходы, связанные с небольшим числом промежуточных шин, а сложные - назначать на выходы, связанные с большим числом промежуточных шин. Кроме того, каждая макроячейка допускает программирование логического уровня выходного сигнала благодаря наличию в архитектуре макроячейки вентиля Исключающее ИЛИ с программируемой связью одного входа с "землёй". Поэтому из двух функций yi или ¯yi для реализации можно выбрать наиболее подходящую (например, которая требует для реализации меньше промежуточных шин), а необходимый вид функции на выходе PAL образуется путём программирования логического уровня выходного сигнала. Макроячейки с двумя обратными связями допускают одновременное использование в двух целях: для реализации промежуточных функций и для приёма входных переменных.
Рисунок 2. Обобщённая структура универсальных PAL
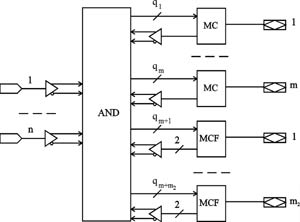
Рисунок 3. Обобщённая структура выходной макроячейки универсальных PAL с двумя обратными связями

Универсальную PAL будем характеризовать параметрами n, m и m2, а также множеством Q = {q1,...,qk}, где qj - число промежуточных шин, подсоединяемых к макроячейке MCj, qj € Q, j = 1,k, k = m + m2. СБФ допускает тривиальную реализацию на универсальной PAL при выполнении условий:
N <= k; (2)
L <= n + k – N,
а также, если для каждой функции yi, yi € Y, найдётся значение qj, qj € Q, такое, что
Q(i) <= qj (3)
где Q( ![]() i) = min(Q(yi),Q(
i) = min(Q(yi),Q(![]() i)), причём разным функциям yi, yi € Y, должны соответствовать различные значения qj, qj € Q.
i)), причём разным функциям yi, yi € Y, должны соответствовать различные значения qj, qj € Q.
Возможности CPLD
Структура CPLD представляет собой совокупность функциональных блоков, объединяемых матрицей переключений SM. Архитектура функциональных блоков (рис. 4) во многом подобна архитектуре универсальных PAL. Отличия заключаются в том, что все выходные макроячейки имеют две обратные связи, а промежуточные шины макроячейкам назначаются с помощью распределителя (allocator). Некоторые макроячейки CPLD не имеют связи с внешним выводом. Такие макроячейки называются скрытыми. Скрытые макроячейки имеют только одну обратную связь.
Рисунок 4. Обобщённая структура функционального блока CPLD и его взаимодействие с матрицей переключений

Каждый функциональный блок CPLD будем характеризовать числом входов n; выходных макроячеек m; общим числом макроячеек r, из которых r-m являются скрытыми; суммарным числом промежуточных шин функционального блока q![]() и максимальным числом промежуточных шин qmax, которые могут быть подсоединены к одной макроячейке. Кроме того, общая структура CPLD характеризуется числом E функциональных блоков и числом dI "чистых" входов.
и максимальным числом промежуточных шин qmax, которые могут быть подсоединены к одной макроячейке. Кроме того, общая структура CPLD характеризуется числом E функциональных блоков и числом dI "чистых" входов.
Отметим некоторые особенности синтеза комбинационных схем на CPLD, обусловленные их архитектурными свойствами:
Пусть Yt - подмножество функций, реализуемых t-м функциональным блоком CPLD, Yt ![]() Y, t = 1,T, T <= E. СБФ Y допускает тривиальную реализацию на одном CPLD, если выполняются условия:
Y, t = 1,T, T <= E. СБФ Y допускает тривиальную реализацию на одном CPLD, если выполняются условия:
N <= m·E;
L <= dI + m·E – N; (4)
Q(yi) <= qmax, для всех yi, yi € Y,
а также, если для каждого подмножества Yt, t = 1,T, имеет место:
|Xt| <= n;
|Yt| <= m;nbsp; (5)
Qt <= q,
где ![]() ;
; ![]() ; X(yi) - множество аргументов функции yi, yi € Y.
; X(yi) - множество аргументов функции yi, yi € Y.
Условия (4) и (5) остаются справедливыми и для случая, когда промежуточные шины между макроячейками CPLD распределяются кластерами. Для этого достаточно положить:
Q(i) := ]Q(
i)/qCL[;
qmax := ]qmax/qCL[;
q:= ]q
/qCL[,
где ]A[ - наименьшее целое, большее или равное A.
Характеристика предлагаемых методов синтеза
Традиционно методы синтеза комбинационных схем на ПЛИС включают следующие последовательно выполняемые этапы:
Недостатки традиционного подхода заключаются в следующем:
Основные отличия предлагаемого подхода к синтезу комбинационных схем на ПЛИС от традиционного заключаются в следующем:
Снижение стоимости реализации комбинационных схем в предлагаемых методах синтеза достигается за счёт эффективного использования:
Более подробно новые методы синтеза комбинационных схем будут рассмотрены в следующих номерах журнала.
Литература