Первоисточник: http://www.sgu.ru/ie/mehmat/odfka/r2/R2-1.htm
В статье рассматривается введение в теорию детерминированных автоматов: основные определения, формулы, примеры.
Построение конечного детерминированного автомата
Конечным детерминированным автоматом
(к.д.а.) Мили называется система ![]() , где
, где ![]() ,
, ![]() ,
, ![]() – конечные множества (алфавиты), а
– конечные множества (алфавиты), а ![]()
![]() – функции, определенные на этих
множествах. Множества X, Y называются соответственно алфавитом
состояний, входным и выходным алфавитом, d
– функцией переходов, l
– функцией выходов. Если, кроме того, в автомате A выделено одно
состояние, называемое начальным (обычно будет считаться, что это
– функции, определенные на этих
множествах. Множества X, Y называются соответственно алфавитом
состояний, входным и выходным алфавитом, d
– функцией переходов, l
– функцией выходов. Если, кроме того, в автомате A выделено одно
состояние, называемое начальным (обычно будет считаться, что это ![]() ), то автомат называется
инициальным. К.д.а. А называется автоматом Мура, если его
функция выходов зависит только от состояний, т. е.
), то автомат называется
инициальным. К.д.а. А называется автоматом Мура, если его
функция выходов зависит только от состояний, т. е.
Функцию выходов автоматов Мура считают
одноаргументной функцией (![]() ) и называют функцией отметок.
) и называют функцией отметок.
Будучи определенными на конечных множествах функции d и l могут быть заданы с помощью таблицы, которая называется таблицей переходов-выходов (рис. 2.1).
| x1 | . . . | xj | . . . | xk | |
| s0 s1 |
|||||
| si | 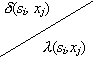 |
||||
В верхнем треугольнике каждой клеточки
таблицы записывается значение ![]() функции переходов, в нижнем – значение
функции переходов, в нижнем – значение
![]() функции выходов.
функции выходов.
Поскольку для автомата Мура значение функции выходов определяется только состоянием, то для каждой строки значение функции выходов (в нижнем треугольнике) одно и то же, поэтому это значение часто выносится в отдельный столбец (рис. 2.2).
| x1 | . . . | xj | . . . | xk | |||
| s0 s1 |
l (s0 ) | ||||||
| si | d (si,xj ) | l (si ) | |||||
| l (sr-1 ) |
Другой распространенный способ задания
автомата – с помощью диаграммы Мура, фигуры на плоскости (графа),
состоящей из вершин, изображаемых точками, и дуг, изображаемых отрезком прямой
со стрелкой. Вершины взаимно однозначно соответствуют состояниям автомата, а
дуги – входным символам. Из каждой вершины исходит к дуг (к –
число символов входного алфавита). Из вершины ![]() проводится дуга в вершину
проводится дуга в вершину ![]()
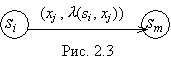 в том и только в том случае, когда
в том и только в том случае, когда ![]() для некоторого
для некоторого ![]() . Эта дуга помечается парой
. Эта дуга помечается парой ![]() (рис.2.3).
(рис.2.3).
Начальное состояние в инициальном автомате помечается символом *.

В автомате Мура значение функции
выходов (отметка) ставится при вершине, а дуги помечаются только ![]()
(рис. 2.4).
Конечный детерминированный автомат
может служить математической моделью технического устройства с конечной памятью,
функционирующего в дискретном времени ![]() Сигналы, поступающие на вход устройства, кодируются
буквами входного алфавита X, на выходе сигналы обозначаются буквами
выходного алфавита Y. Устройству, имеющему n входов, отвечает
автомат со структурным входным алфавитом
Сигналы, поступающие на вход устройства, кодируются
буквами входного алфавита X, на выходе сигналы обозначаются буквами
выходного алфавита Y. Устройству, имеющему n входов, отвечает
автомат со структурным входным алфавитом ![]() . Состояние автомата характеризует вариант
распределения памяти дискретного устройства.
. Состояние автомата характеризует вариант
распределения памяти дискретного устройства.
Работа к.д.а. как абстрактного (воображаемого) устройства может быть описана следующим образом.
В каждый момент t дискретного
времени автомат, находясь в некотором состоянии s(t) из множества
S, под действием входного сигнала x(t) из множества
X выдает выходной сигнал y(t) из множества Y
согласно функции выходов l,
а затем меняет свое состояние на s(t+1) согласно функции переходов
d.
В момент t=1 автомат находится в некотором начальном состоянии ![]() . Таким образом, работа автомата может
быть описана системой равенств:
. Таким образом, работа автомата может
быть описана системой равенств:
 для автомата Мили
или
для автомата Мили
или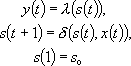 для автомата Мура.
для автомата Мура.
Указанные системы равенств называются каноническими уравнениями. Описывая некоторый дискретный процесс преобразования информации, модель к.д.а. может быть использована для построения функциональной схемы устройства, осуществляющего этот процесс.
Рассмотрим процедуру построения схемы устройства, содержащую этапы:
1) построение к.д.а. на основе какого-либо описания дискретного процесса;
2) минимизация автомата;
3) построение канонической таблицы и канонических уравнений;
4) минимизация канонических уравнений;
5) построение схемы устройства.
В примерах построения к.д.а. преобразование информации задается формулами.
Пример 1
где
Построить автомат – это значит
определить множества S, X, Y и задать функции переходов и
выходов (построить их таблицу или диаграмму Мура). Ясно, что для данной задачи
![]() .
.
Для определения множества состояний
автомата необходимо уяснить содержательный смысл и назначение понятия состояние,
а для этого удобно представить себе функционирование автомата как работу
абстрактного устройства. В моменты дискретного времени, отмеченные числами
натурального ряда ![]() , на вход автомата поступает сигнал
x(t), на выходе наблюдается сигнал y(t). После
преобразования сигнала x(t) это значение теряется.
, на вход автомата поступает сигнал
x(t), на выходе наблюдается сигнал y(t). После
преобразования сигнала x(t) это значение теряется.
Иначе говоря, в любой тактовый момент
x(t) в устройстве нет как таковой информации о сигналах во все
предыдущие моменты, т. е. ![]() Поэтому, если при вычислении значения функции по
формуле необходима информация об этих тактовых моментах, то ее нужно
предварительно каким-либо образом “запомнить”. В этом и состоит содержательное
назначение состояний.
Поэтому, если при вычислении значения функции по
формуле необходима информация об этих тактовых моментах, то ее нужно
предварительно каким-либо образом “запомнить”. В этом и состоит содержательное
назначение состояний.
Итак, состояния – вспомогательные объекты, которые подбираются таким образом, чтобы в совокупности с входным значением x(t) однозначным образом определить выходное значение y(t). Обычно состояния обозначают (кодируют) ту необходимую для вычисления y(t) информацию, которая поступила до момента t.
Учитывая, что состояния – вспомогательные объекты, их можно описывать словесно, однако это не является обязательным.
Анализируя формулу рассматриваемой функции, видно, что кроме текущего входного значения x(t) каждое выходное значение y(t) зависит от входного значения в момент, непосредственно предшествующий моменту t, поэтому логично рассмотреть состояния, соответствующие различным значениям x(t-1) и описать их следующим образом:
![]() – “на предыдущем такте поступил 0”,
– “на предыдущем такте поступил 0”,
![]() – “на предыдущем такте поступила 1”.
– “на предыдущем такте поступила 1”.
| 0 | 1 | |
| s1 |  |
 |
| s1 |  |
 |
После этого можно начать заполнять таблицу перходов–выходов автомата (рис. 2.5).
| 0 | 1 | |
| s1 |  |
 |
| s1 |  |
 |
Нижние треугольники каждой клеточки
таблицы содержат значения y(t), которые вычисляются по формуле
![]() , причем значение x(t-1)
определяется на основе значения состояния s(t) в левой части
соответствующей строки, а значение x(t) есть верхняя часть
соответствующего столбца. Итак, для нижнего треугольника 1-й клеточки 1-й строки
, причем значение x(t-1)
определяется на основе значения состояния s(t) в левой части
соответствующей строки, а значение x(t) есть верхняя часть
соответствующего столбца. Итак, для нижнего треугольника 1-й клеточки 1-й строки
![]() , так как
, так как ![]() (на предыдущем такте t-1 поступил
0) (рис.2. 6).
(на предыдущем такте t-1 поступил
0) (рис.2. 6).
Вторая нижняя клеточка 1- й строки
таблицы содержит ![]() , так как
, так как ![]() ,
, ![]() .
.
Аналогично для второй строки в нижнем
треугольнике 1-й клеточки ![]() , так как
, так как ![]() (на предыдущем такте
(на предыдущем такте ![]() поступила 1), а
поступила 1), а ![]() , для 2-й клеточки
, для 2-й клеточки ![]() .
.
Начинаем заполнять значения функции
переходов. В верхний треугольник каждой строки помещается значение ![]() , т.е. состояние на следующем такте. Выбирая в
качестве состояния s(t+1) одно из значений
, т.е. состояние на следующем такте. Выбирая в
качестве состояния s(t+1) одно из значений ![]() или
или ![]() , учитываем, что для такта t+1
предыдущим тактом является такт t, поэтому значение состояния
s(t+1) определяется очередным значением x(t),
которое располагается в верхней части соответствующего столбца. В верхнем
треугольнике 1-й клеточки 1-й строки имеем
, учитываем, что для такта t+1
предыдущим тактом является такт t, поэтому значение состояния
s(t+1) определяется очередным значением x(t),
которое располагается в верхней части соответствующего столбца. В верхнем
треугольнике 1-й клеточки 1-й строки имеем ![]() , поскольку
, поскольку ![]() , а потому для такта t+1 это и есть
поступившее предыдущее значение (табл. 2.1).
, а потому для такта t+1 это и есть
поступившее предыдущее значение (табл. 2.1).
| 0 | 1 | |
| s1 |  |
 |
| s1 |  |
 |
Для второй клеточки 1-й строки ![]() , так как
, так как ![]() . Аналогично заполняется 2-я строка: 1-я
клеточка содержит
. Аналогично заполняется 2-я строка: 1-я
клеточка содержит ![]() , 2-я –
, 2-я – ![]() . Таким образом, в том или ином состоянии
. Таким образом, в том или ином состоянии
![]() или
или ![]() запоминается поступившее входное значение
x(t) для последующего такта.
запоминается поступившее входное значение
x(t) для последующего такта.
Указанная таблица описывает работу
автомата на всех тактах, начиная со второго. Для завершения построения автомата
необходимо обеспечить формирование значения ![]() на 1-м такте так, как это указано в
первоначальной формуле. Эта задача решается выбором того или иного начального
состояния. Для начала проанализируем таблицу построенного автомата и решим,
можно ли в качестве начального состояния выбрать одно из состояний
на 1-м такте так, как это указано в
первоначальной формуле. Эта задача решается выбором того или иного начального
состояния. Для начала проанализируем таблицу построенного автомата и решим,
можно ли в качестве начального состояния выбрать одно из состояний ![]() или
или ![]() .
.
Начальное состояние ![]() должно обеспечивать выполнение двух условий:
должно обеспечивать выполнение двух условий:
1) при ![]() значение функции выходов y(1) должно быть
равно 0 независимо от входного значения x(t). Иначе говоря, нижние
треугольники строки для состояния
значение функции выходов y(1) должно быть
равно 0 независимо от входного значения x(t). Иначе говоря, нижние
треугольники строки для состояния ![]() должны все содержать нули;
должны все содержать нули;
2) под действием входного значения
x(t) состояние ![]() должно переходить в такое состояние
s(t+1), которое бы “запоминало” значение x(t) и
обеспечивало бы правильную работу автомата для тактов
должно переходить в такое состояние
s(t+1), которое бы “запоминало” значение x(t) и
обеспечивало бы правильную работу автомата для тактов ![]()
В таблице нет состояния, которое
удовлетворяло бы первому условию, поэтому к множеству S состояний
добавляется новое состояние ![]() , а к таблице приписывается новая строка,
которая заполняется таким образом, чтобы удовлетворялись условия 1) и 2) (табл.
2.2).
, а к таблице приписывается новая строка,
которая заполняется таким образом, чтобы удовлетворялись условия 1) и 2) (табл.
2.2).
Автомату с таблицей 2.2 соответствует диаграмма Мура (рис. 2.7).

| 0 | 1 | |
| s1 |  |
 |
| s2 |  |
 |
| * s0 |  |
 |
Замечание. При задании выходного
значения на 1-м такте в качестве начального состояния можно было бы взять состояние
![]() , тогда окончательная таблица автомата
приняла бы вид табл. 2.3.
, тогда окончательная таблица автомата
приняла бы вид табл. 2.3.
| 0 | 1 | |
| s1 | 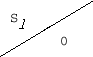 |
 |
| * s2 |  |
 |
Символом * отмечают начальное состояние.
Пример 2
Из условия задачи X = Y = E2.
Для определения множества состояний необходимо понять, от чего зависит очередное выходное значение y(t) кроме значения x(t). На первый взгляд для вычисления y(t) необходимо “помнить” значения входной переменной на всех предыдущих тактах. Однако анализ формулы и свойство операции Ú позволяют сделать вывод, что помимо x(t)для вычисления y(t) имеет лишь значение, встречалась ли хотя бы одна единица среди значений x(1), x(2), ... , x(t – 1). При положительном ответе все выражение y(t) обращается в 1, при отрицательном – y(t) определяется значением x(t).
Таким образом, естественно ввести в рассмотрение два состояния, которые могут быть описаны следующим образом:
![]() – “ни на одном из предыдущих тактов
единица не появлялась”;
– “ни на одном из предыдущих тактов
единица не появлялась”;
![]() – “на одном из предыдущих тактов
появилась единица ”.
– “на одном из предыдущих тактов
появилась единица ”.
Таблица переходов-выходов для автомата
содержит строки с состояниями ![]() и
и ![]() (табл. 2.4).
(табл. 2.4).
| 0 | 1 | |
| s1 | 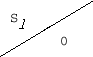 |
 |
| s2 |  |
 |
Первая строка таблицы определяется
ситуацией, когда ни на одном из тактов, предшествующих такту t, на входе
не появлялась единица (состояние ![]() ). Отсюда
). Отсюда![]() . Тогда, если
. Тогда, если ![]() (1-й столбец 1-й строки), то
(1-й столбец 1-й строки), то ![]() , а, если
, а, если ![]() (2-й столбец 1-й строки), то
(2-й столбец 1-й строки), то ![]() . Этим выходным значениям соответствуют
нижние треугольники 1-й строки. Для заполнения значений функции переходов
. Этим выходным значениям соответствуют
нижние треугольники 1-й строки. Для заполнения значений функции переходов ![]() (верхние треугольники) необходимо
вспомнить, что для такта
(верхние треугольники) необходимо
вспомнить, что для такта ![]() такт t также является одним из
предшествующих, поэтому если в состоянии
такт t также является одним из
предшествующих, поэтому если в состоянии ![]() на вход поступает
на вход поступает ![]() , то это определяет
, то это определяет ![]() (единица так и не появилась), а если
поступает
(единица так и не появилась), а если
поступает ![]() , то
, то ![]() .
.
Вторая строка таблицы заполняется для
состояния ![]() , т. е. на одном из предшествующих тактов
такту t поступила 1. Ясно, что
, т. е. на одном из предшествующих тактов
такту t поступила 1. Ясно, что ![]() , а тогда
, а тогда ![]() в обоих столбцах 2-й строки. По этой же
причине устанавливается значение
в обоих столбцах 2-й строки. По этой же
причине устанавливается значение ![]() в обоих столбцах.
в обоих столбцах.
Для завершения построения автомата необходимо выбрать начальное состояние, определяющее значение функции y(t) на 1-м такте работы.
Поскольку ![]() , т. е. выходное значение
y(t) полностью определяется входным значением x(t),
то логично в качестве начального состояния предложить состояние
, т. е. выходное значение
y(t) полностью определяется входным значением x(t),
то логично в качестве начального состояния предложить состояние ![]() . Анализ 1-й строки таблицы показывает,
что в этом случае выходные значения удовлетворяют заданной формуле. Состояния же
“запоминают” для такта 2, поступила или нет единица на 1-м такте. Таким образом,
состояние
. Анализ 1-й строки таблицы показывает,
что в этом случае выходные значения удовлетворяют заданной формуле. Состояния же
“запоминают” для такта 2, поступила или нет единица на 1-м такте. Таким образом,
состояние ![]() устраивает в качестве начального и “по
переходам” и “по выходам”. Таблица и диаграмма Мура автомата приведены в табл.
2.5 и на рис. 2.8 соответственно.
устраивает в качестве начального и “по
переходам” и “по выходам”. Таблица и диаграмма Мура автомата приведены в табл.
2.5 и на рис. 2.8 соответственно.
| 0 | 1 | |
| * s1 | 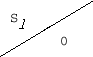 |
 |
| s2 |  |
 |
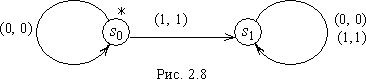
Пример 3
Из способа задания функции следует ![]() . Анализ формулы показывает, что очередное
выходное значение y(t) не зависит от очередного входного значения
x(t) в тот же момент, поэтому к. д. а. будет иметь вид автомата
Мура.
. Анализ формулы показывает, что очередное
выходное значение y(t) не зависит от очередного входного значения
x(t) в тот же момент, поэтому к. д. а. будет иметь вид автомата
Мура.
Поскольку выходное значение
y(t) полностью определяется входным значением, поступившем 2 такта
тому назад, то очевидно, что автомат, в каждый момент t должен “помнить”
это значение ![]() , а поскольку для следующего такта
, а поскольку для следующего такта ![]() выходное значение
выходное значение ![]() будет определяться значением
будет определяться значением ![]() (два такта тому назад), то в каждый момент
t надо “помнить” значение
(два такта тому назад), то в каждый момент
t надо “помнить” значение ![]() также, иначе это значение будет
потеряно.
также, иначе это значение будет
потеряно.
Определяем состояния таким образом, чтобы каждое из них характеризовало определенный вариант “распределения памяти”. Предлагается следующее описание состояний:
![]() – “2 такта тому назад (т. н.) на вход
автомата поступил 0, 1 такт тому назад поступил 0”;
– “2 такта тому назад (т. н.) на вход
автомата поступил 0, 1 такт тому назад поступил 0”;
![]() – “2 такта т. н. на вход автомата
поступил 0, 1 такт т. н. поступила
1”;
– “2 такта т. н. на вход автомата
поступил 0, 1 такт т. н. поступила
1”;
![]() – “2 такта т. н. на вход автомата
поступила 1, 1 такт т. н. поступил 0”;
– “2 такта т. н. на вход автомата
поступила 1, 1 такт т. н. поступил 0”;
![]() – “2 такта т. н. на вход автомата
поступила 1, 1 такт т. н. поступила 1”;
– “2 такта т. н. на вход автомата
поступила 1, 1 такт т. н. поступила 1”;
Заполним соответствующие строки таблицы переходов и выходов (табл. 2.6).
Содержимое столбца для функции выходов
полностью определяется состоянием. В состояниях ![]() и
и ![]()
![]() , поскольку эти состояния соответствуют
, поскольку эти состояния соответствуют
![]() аналогично в состоянии
аналогично в состоянии ![]() и
и ![]()
![]() . Заполним теперь таблицу переходов.
Вспомним еще раз, что в клеточках таблицы записывается значение состояния в
момент t+1. По отношению к этому моменту 2 такта тому назад был момент
t –1 и то, что поступило на этом такте можно определить через состояние:
в состоянии
. Заполним теперь таблицу переходов.
Вспомним еще раз, что в клеточках таблицы записывается значение состояния в
момент t+1. По отношению к этому моменту 2 такта тому назад был момент
t –1 и то, что поступило на этом такте можно определить через состояние:
в состоянии ![]() и
и ![]() – это 0, в состоянии
– это 0, в состоянии ![]() ,
, ![]() – 1. Один такт тому назад для t+1
был такт t, и значение входной переменной на этом такте – это значение
x(t) в верхней части соответствующего столбца. Таким образом, для
первой клеточки 1-й строки имеем: 2 такта т. н. поступил 0, 1 такт т. н. – 0.
Этой ситуации соответствует состояние
– 1. Один такт тому назад для t+1
был такт t, и значение входной переменной на этом такте – это значение
x(t) в верхней части соответствующего столбца. Таким образом, для
первой клеточки 1-й строки имеем: 2 такта т. н. поступил 0, 1 такт т. н. – 0.
Этой ситуации соответствует состояние ![]() . Второй клеточке 1-й строки соответствует
ситуация: 2 такта т. н. поступил 0 (состояние в строке
. Второй клеточке 1-й строки соответствует
ситуация: 2 такта т. н. поступил 0 (состояние в строке ![]() ), 1 такт т. н. – 1 (значение столбца).
Получаем состояние
), 1 такт т. н. – 1 (значение столбца).
Получаем состояние ![]() . Для второй строки: состояние
. Для второй строки: состояние ![]() говорит о том, что 2 такта т. н. для
такта t+1 поступила 1, а 1 такт т. н.
для первой клеточки – это 0, для второй – 1. Тогда 2-я строка заполняется
соответственно состояниями
говорит о том, что 2 такта т. н. для
такта t+1 поступила 1, а 1 такт т. н.
для первой клеточки – это 0, для второй – 1. Тогда 2-я строка заполняется
соответственно состояниями ![]() и
и ![]() и т. д. Аналогично в 3-й строке имеем
и т. д. Аналогично в 3-й строке имеем
![]() и
и ![]() , в 4-й –
, в 4-й – ![]() и
и ![]() .
.
| 0 | 1 | |||
| s1 | s1 | s2 | 0 | |
| s2 | s3 | s4 | 0 | |
| s3 | s1 | s2 | 1 | |
| s4 | s3 | s4 | 1 |
Выберем теперь начальное состояние автомата, которое дало бы необходимые выходные значения на такте 1 и 2, а также обеспечило бы запоминание необходимой информации таким образом, чтобы, начиная с такта 3, автомат работал согласно уже заполненной таблице.
Итак, начальное состояние ![]() должно удовлетворять следующим требованиям:
должно удовлетворять следующим требованиям:
1) на такте 1 выходное значение y(1) должно быть равно 1 согласно начальному условию;
2) на такте 2 ![]() ;
;
3) входное слово 00 должно переводить
состояние ![]() в состояние
в состояние ![]() , которому соответствует описание: “2
такта т. н. – 0, 1 такт т. н. – 0”;
, которому соответствует описание: “2
такта т. н. – 0, 1 такт т. н. – 0”;
4) аналогично слово 01 переводит ![]() в состояние
в состояние ![]() ;
;
5) слово 10 переводит ![]() в состояние
в состояние ![]() ;
;
6) слово 11 переводит ![]() в состояние
в состояние ![]() .
.
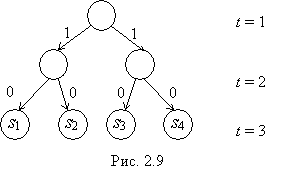
Все эти условия удобно графически
изобразить в виде диаграммы (дерева), в котором вершины соответствуют
состояниям, а дуги – входному сигналу на соответствующем такте (рис. 2.9).
Корень дерева (верхний кружок) соответствует начальному состоянию ![]() . Левая дуга, исходящая из каждой вершины,
соответствует входному значению
. Левая дуга, исходящая из каждой вершины,
соответствует входному значению ![]() , правая –
, правая – ![]() . Эти значения на дуге не
отмечаются, но подразумеваются. Начальная вершина дерева вместе с дугами,
исходящими из нее, образуют 1-й ярус, на котором отмечается информация,
относящаяся к первому такту работы автомата. Пометки на дугах соответствуют
выходному значению y(t), если автомат находился в начальном
состоянии, а на вход поступает значение x(t), определяемое
направлением дуги. Поскольку
. Эти значения на дуге не
отмечаются, но подразумеваются. Начальная вершина дерева вместе с дугами,
исходящими из нее, образуют 1-й ярус, на котором отмечается информация,
относящаяся к первому такту работы автомата. Пометки на дугах соответствуют
выходному значению y(t), если автомат находился в начальном
состоянии, а на вход поступает значение x(t), определяемое
направлением дуги. Поскольку ![]() то обе дуги 1-го яруса помечаются
единицами (независимо от значения x(t)).
то обе дуги 1-го яруса помечаются
единицами (независимо от значения x(t)).
Вершины, являющиеся концами дуг 1-го
яруса, вместе с дугами, исходящими из них, образуют 2-й ярус, на котором
отмечается информация, относящаяся ко 2-му такту работы автомата. Левая вершина
2-го яруса – это состояние, в которое попадает начальное состояние ![]() по входному значению
по входному значению ![]() , правая – состояние, в которое попадает
, правая – состояние, в которое попадает
![]() по
по ![]() . Все эти состояния первоначально
неизвестны, поэтому им соответствуют пустые кружочки.
. Все эти состояния первоначально
неизвестны, поэтому им соответствуют пустые кружочки.
Поскольку пометка каждой дуги есть
выходное значение y(t), соответствующее входному значению
x(t), определяемому направлением дуги и вершиной, то все дуги 2-го
яруса помечаются 0 (по условию ![]() независимо от
x(t)).
независимо от
x(t)).

Вершины, являющиеся концами дуг 2-го
яруса, относятся к 3-му ярусу и им соответствуют состояния, в которое попадает
автомат под действием слов 00 (1-я вершина слева), 01 (2-я вершина), 10 (3-я
вершина) и 11. Таким образом, на 3-м ярусе состояния (вершины) определены.
Учитывая это и двигаясь снизу вверх по дереву можно начать подбирать остальные
состояния на основе имеющейся информации. Чтобы заполнить левый кружочек 2-го
яруса, нужно подобрать такое состояние, будучи в котором автомат на выходе
даст![]() независимо от x(t) (нулевые
пометки дуг) и, кроме того, по нулевому значению x(t) это
состояние переходит в состояние
независимо от x(t) (нулевые
пометки дуг) и, кроме того, по нулевому значению x(t) это
состояние переходит в состояние ![]() , а по единичному – в
, а по единичному – в ![]() (концы соответствующих дуг). Анализ
таблицы автомата показывает, что таким состоянием может быть состояние
(концы соответствующих дуг). Анализ
таблицы автомата показывает, что таким состоянием может быть состояние ![]() . Состояние, соответствующее правому
кружочку 2-го яруса подбирается так, чтобы выходное значение также было равно 0,
а переходы соответственно в
. Состояние, соответствующее правому
кружочку 2-го яруса подбирается так, чтобы выходное значение также было равно 0,
а переходы соответственно в ![]() и
и ![]() по 0 или 1. В таблице автомата таким
условиям удовлетворяет состояние
по 0 или 1. В таблице автомата таким
условиям удовлетворяет состояние ![]() (рис.2.10). Осталось подобрать начальное
состояние. В нем на выходе автомат дает единицы, а переходы –
(рис.2.10). Осталось подобрать начальное
состояние. В нем на выходе автомат дает единицы, а переходы – ![]() и
и ![]() по 0 или 1 соответственно. Очевидно, что
в качестве
по 0 или 1 соответственно. Очевидно, что
в качестве ![]() можно взять
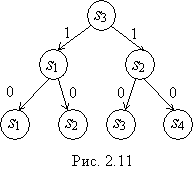
можно взять ![]() (рис. 2.11).
(рис. 2.11).
Окончательная таблица и соответствующая диаграмма Мура представлены в табл. 2.7 и на рис. 2.12.

| 0 | 1 | |||
| s1 | s1 | s2 | 0 | |
| s2 | s3 | s4 | 0 | |
| s3 | s1 | s2 | 1 | |
| s4 | s3 | s4 | 1 |
В диаграмме Мура жирно выделены метки вершин, соответствующие выходным значениям. Метки на дугах есть соответствующие входные значения x(t). Можно проверить, что эта диаграмма идентична диаграмме Мура, построенной с использованием аппарата деревьев для аналогичного примера (см. гл.1, параграф 1.3) с точностью до обозначения состояний.
В рассматриваемой задаче не было необходимости вводить новые состояния. Если при подборе состояний в таблице автомата нет состояния, удовлетворяющего необходимым условиям, то добавляются новые и к таблице дописываются новые строки, как это было показано в примере 1) этого параграфа. При этом при подборе состояний также удобно двигаться снизу вверх, на каждом шаге используя вновь полученную информацию
Пример 4
Дискретный процесс преобразования
информации, описываемый приведенной формулой, может быть реализован устройством
с двумя входными каналами, по первому поступают значения ![]() , по второму -
, по второму - ![]() в каждый момент
в каждый момент ![]() Очевидно, что
Очевидно, что ![]()
Для определения множества состояний проанализируем формулу. Видно, что очередное значение y(t), зависит от значения входной переменной, поступающей по первому входному каналу в момент, предшествующий моменту t. А это значение может быть 0 или 1. Таким образом, естественно рассмотреть два состояния:
![]() - "на предыдущем такте по первому
входному каналу поступил 0";
- "на предыдущем такте по первому
входному каналу поступил 0";
![]() – "на предыдущем такте по первому
входному каналу поступила 1".
– "на предыдущем такте по первому
входному каналу поступила 1".
Заполняем таблицу автомата (табл. 2.8).
| (0,0) | (0,1) | (1,0) | (1,1) | |
| s1 |  |
 |
 |
 |
| s2 |  |
 |
 |
 |
Первая строка таблицы соответствует
состоянию ![]() , а значит ситуации, когда
, а значит ситуации, когда ![]() , тогда по свойству операции Ú
выходное значение y(t) полностью определяется значением второй координаты
входной переменной
, тогда по свойству операции Ú
выходное значение y(t) полностью определяется значением второй координаты
входной переменной ![]() , которая находится в верхней части
каждого столбца. Поэтому выходные значения в 1-й строке слева направо будут
, которая находится в верхней части
каждого столбца. Поэтому выходные значения в 1-й строке слева направо будут ![]()
![]() . Вторая строка таблицы соответствует
состоянию
. Вторая строка таблицы соответствует
состоянию ![]() , а значит ситуации, когда
, а значит ситуации, когда ![]() , а потому согласно формуле выходные
значения
, а потому согласно формуле выходные
значения ![]() независимо от значения входной переменной
(т. е. столбца), поэтому выходные значения во второй строке все равны 1.
независимо от значения входной переменной
(т. е. столбца), поэтому выходные значения во второй строке все равны 1.
При заполнении значений функции
переходов ![]() учитываем, что предыдущим тактом для
такта t +1 является такт t, а поэтому значение первой координаты
входной пары (верхняя часть каждого столбца) однозначно определяет следующие
состояния: для первых двух столбцов первая нулевая компонента определяет
состояние
учитываем, что предыдущим тактом для
такта t +1 является такт t, а поэтому значение первой координаты
входной пары (верхняя часть каждого столбца) однозначно определяет следующие
состояния: для первых двух столбцов первая нулевая компонента определяет
состояние ![]() в обеих строках, в 3-м и 4-м столбцах
вторая единичная компонента дает состояние
в обеих строках, в 3-м и 4-м столбцах
вторая единичная компонента дает состояние ![]() для обеих строк.
для обеих строк.
Подберем начальное состояние, которое должно удовлетворять следующим условиям:
1) выходное значение на 1-м такте
согласно условию должно быть равно 1, ![]() ;
;
2) по входным наборам (0, 0), (0, 1)
начальное состояние ![]() должно переходить в состояние
должно переходить в состояние ![]() , которое “запоминает” первую координату
для такта t=2
, которое “запоминает” первую координату
для такта t=2
3) по входным наборам (1, 0), (1, 1)
![]() переходит в состояние
переходит в состояние ![]() , “запоминающее” единицу в первой
координате входных наборов.
, “запоминающее” единицу в первой
координате входных наборов.
Анализ таблицы показывает, что таким
условиям удовлетворяет состояние ![]() . Оно и выбирается в качестве начального.
Окончательная таблица и диаграмма Мура представлены в табл. 2.9 и на
рис.2.13.
. Оно и выбирается в качестве начального.
Окончательная таблица и диаграмма Мура представлены в табл. 2.9 и на
рис.2.13.
| (0,0) | (0,1) | (1,0) | (1,1) | |
| s1 |  |
 |
 |
 |
| * s2 |  |
 |
 |
 |
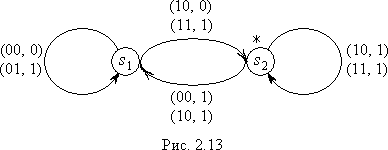
Замечание. При выборе начального
условия ![]() в таблице не нашлось бы необходимого
начального состояния
в таблице не нашлось бы необходимого
начального состояния ![]() . В этом случае к таблице следует добавить строку,
содержащую новое начальное состояние и определить необходимые переходы и выходы.
Таблица автомата в этом случае имеет вид табл. 2.10.
. В этом случае к таблице следует добавить строку,
содержащую новое начальное состояние и определить необходимые переходы и выходы.
Таблица автомата в этом случае имеет вид табл. 2.10.
![]()
![]()
![]()
| (0,0) | (0,1) | (1,0) | (1,1) | |
| s1 | 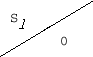 |
 |
 |
 |
| s2 |  |
 |
 |
 |
| * s0 | 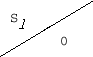 |
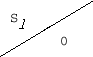 |
 |
 |
Пример 5
Дискретный процесс описан функцией поразрядного сложения двух бесконечных двоичных слов согласно обычному алгоритму сложения чисел, но в двоичной системе счисления.
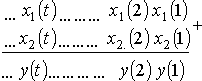
Очередной разряд суммы y(t) вычисляется по формуле:

Описанный дискретный процесс может быть
реализован техническим устройством, называемым сумматором последовательного
действия. В каждый момент t на вход сумматора поступает входное значение
x(t), содержащее две компоненты: ![]() На выходе формируется очередное значение
суммы y(t).
На выходе формируется очередное значение
суммы y(t).
Отсюда следует, что для автомата,
реализующего этот процесс, справедливо ![]()
Как обычно, состояния описывают то, что помимо входных значений в момент t определяет выходное значение y(t). Поскольку кроме входных значений в момент t выходное значение зависит от того, есть или нет перенос из предыдущего разряда, логично ввести состояния:
![]() – “нет переноса из предыдущего
разряда”;
– “нет переноса из предыдущего
разряда”;
![]() – “есть перенос из предыдущего
разряда”.
– “есть перенос из предыдущего
разряда”.
Тогда таблица автомата имеет вид табл. 2.11.
| (0,0) | (0,1) | (1,0) | (1,1) | |
| s1 | 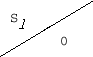 |
 |
 |
 |
| * s2 |  |
 |
 |
 |
Первая строка таблицы соответствует
состоянию ![]() , когда нет переноса из предыдущего
разряда. В этом случае выходное значение y(t) есть сумма по mod 2
компонент входной пары в верхней части каждого столбца. Поэтому в 1-й строке
слева направо имеем:
, когда нет переноса из предыдущего
разряда. В этом случае выходное значение y(t) есть сумма по mod 2
компонент входной пары в верхней части каждого столбца. Поэтому в 1-й строке
слева направо имеем:
![]() .
.
![]() , когда есть перенос из предыдущего
разряда, поэтому при вычислении суммы надо добавлять 1. Тогда слева направо
имеем:
, когда есть перенос из предыдущего
разряда, поэтому при вычислении суммы надо добавлять 1. Тогда слева направо
имеем:
![]()
При определении состояния
s(t +1) учитываем, будет ли перенос из разряда t в
разряд t +1 при вычислении суммы y(t). Ясно, что в 1-й
строке перенос будет, когда складываются две единицы в последнем столбце. Там
устанавливается состояние ![]() , в остальных клеточках –
, в остальных клеточках – ![]() , так как переноса нет.
, так как переноса нет.
Во 2-й строке, поскольку при вычислении
y(t) еще добавляется 1, то перенос будет во всех случаях, кроме
первого, когда складываются два нуля: ![]() и переноса нет.
и переноса нет.
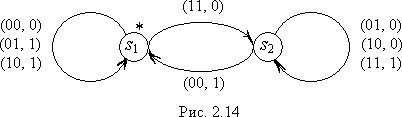
Итак, в рассматриваемой задаче в
состоянии “запоминается”, есть ли перенос. Очевидно тогда, что начальным
состоянием должно быть состояние ![]() , так как при вычислении y(1) нет
предыдущего разряда. В итоге получаем таблицу и диаграмму Мура, представленные в
табл. 2.12 и на рис.2.14.
, так как при вычислении y(1) нет
предыдущего разряда. В итоге получаем таблицу и диаграмму Мура, представленные в
табл. 2.12 и на рис.2.14.
| (0,0) | (0,1) | (1,0) | (1,1) | |
| * s1 | 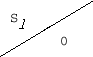 |
 |
 |
 |
| s2 |  |
 |
 |
 |