Первоисточник: http://www.sgu.ru/ie/mehmat/odfka/r2/R2-2.htm
В данной статье рассматриваются существующие методы минимизации конечной структуры управляющих автоматов.
Минимизация конечных автоматов
Пусть ![]() – автомат Мили. Расширим действие функций d
и l
на слова в алфавите X следующим образом:
– автомат Мили. Расширим действие функций d
и l
на слова в алфавите X следующим образом:
![]() ,
,![]() ,
,
![]() .
.
Функция ![]() называется расширенной функцией
переходов.
называется расширенной функцией
переходов.
![]()
![]() .
.
Функция ![]() называется расширенной функцией выходов.
Согласно приведенному определению она отмечает последний переход в автомате.
называется расширенной функцией выходов.
Согласно приведенному определению она отмечает последний переход в автомате.
Пусть ![]() , i = 1, 2 – автоматы с одинаковыми входными
и выходными алфавитами. Состояния
, i = 1, 2 – автоматы с одинаковыми входными
и выходными алфавитами. Состояния ![]() автомата А1 и
автомата А1 и ![]() автомата А2 называются
неотличимыми (эквивалентными) тогда и только тогда, когда для
любого слова
автомата А2 называются
неотличимыми (эквивалентными) тогда и только тогда, когда для
любого слова ![]() справедливо
справедливо
![]() .
.
Отсюда следует, что при подаче на вход
автоматов любого слова ![]() выходные слова автоматов, находящихся
соответственно в состоянии
выходные слова автоматов, находящихся
соответственно в состоянии ![]() и
и ![]() совпадают (состояния не различаются по
выходу).
совпадают (состояния не различаются по
выходу).
В частности, может быть А1= А2, и речь будет идти о неотличимых состояниях одного автомата. Отношение неотличимости на множестве состояний одного автомата является отношением эквивалентности. Оно разбивает множество всех состояний на непересекающиеся классы. Каждый класс содержит все неотличимые между собой состояния.
Автоматы А1 и
А2 называются неотличимыми (эквивалентными)
тогда и только тогда, когда для любого состояния ![]() автомата А1 существует
эквивалентное ему состояние
автомата А1 существует
эквивалентное ему состояние ![]() автомата А2, и для каждого
состояния
автомата А2, и для каждого
состояния ![]() автомата А2 существует
эквивалентное ему состояние
автомата А2 существует
эквивалентное ему состояние ![]() автомата А1. Неотличимые
автоматы осуществляют одно и то же отображение входных слов в выходные.
автомата А1. Неотличимые
автоматы осуществляют одно и то же отображение входных слов в выходные.
Автомат А называется
приведенным, если в нем нет эквивалентных состояний. Известно, что для
любого автомата![]() существует эквивалентный ему приведенный автомат
А. Число состояний в этом автомате является минимальным в классе всех
автоматов, эквивалентных автомату
существует эквивалентный ему приведенный автомат
А. Число состояний в этом автомате является минимальным в классе всех
автоматов, эквивалентных автомату ![]() . Процедура нахождения приведенного (минимального)
автомата
. Процедура нахождения приведенного (минимального)
автомата ![]() для произвольного автомата
для произвольного автомата ![]() называется минимизацией конечного автомата
называется минимизацией конечного автомата
![]() .
.
Для нахождения минимального автомата
множество ![]() всех состояний автомата
всех состояний автомата ![]() разбивается на классы по отношению неотличимости
состояний.
разбивается на классы по отношению неотличимости
состояний.
Пусть ![]() – разбиение на
– разбиение на ![]() , соответствующее отношению неотличимости. Тот
факт, что состояния s и t из
, соответствующее отношению неотличимости. Тот
факт, что состояния s и t из ![]() находятся в одном классе разбиения
находятся в одном классе разбиения ![]() будем обозначать:
будем обозначать: ![]() .
.
Через ![]() будем обозначать класс разбиения
будем обозначать класс разбиения ![]() , содержащий элемент s из
, содержащий элемент s из ![]() .
.
Разбиение ![]() , соответствующе отношению неотличимости, можно
построить согласно следующей процедуре, называемой алгоритмом Мили.
, соответствующе отношению неотличимости, можно
построить согласно следующей процедуре, называемой алгоритмом Мили.
Строится последовательность разбиений
![]() следующим образом:
следующим образом:
Шаг 1.
![]() .
.
Иначе одному классу ![]() принадлежат те состояния s и t,
которые одинаково реагируют на все слова длины 1.
принадлежат те состояния s и t,
которые одинаково реагируют на все слова длины 1.
Шаг к.![]()
В один класс разбиения ![]() объединяются те состояния из класса
объединяются те состояния из класса ![]() , которые по любому сигналу х переходят в
один и тот же класс разбиения
, которые по любому сигналу х переходят в
один и тот же класс разбиения ![]() . Поскольку
. Поскольку ![]() , т. е.
, т. е. ![]() получается из
получается из ![]() измельчением классов, то на шаге к в один
класс объединяются те состояния s и t, которые одинаково реагируют
на все слова длины к, а поскольку для нетривиальных автоматов число
состояний в каждом классе разбиения
измельчением классов, то на шаге к в один
класс объединяются те состояния s и t, которые одинаково реагируют
на все слова длины к, а поскольку для нетривиальных автоматов число
состояний в каждом классе разбиения ![]() не более п -1, то для некоторого шага
не более п -1, то для некоторого шага ![]() окажется
окажется ![]() , т. е. число классов перестает увеличиваться.
Разбиение
, т. е. число классов перестает увеличиваться.
Разбиение ![]() и является искомым разбиением
и является искомым разбиением ![]() , поскольку состояния из одного класса разбиения
, поскольку состояния из одного класса разбиения
![]() одинаково реагируют на слова любой длины.
Для автомата
одинаково реагируют на слова любой длины.
Для автомата ![]() полагают
полагают ![]() , в качестве же множества состояний S
приведенного автомата берется множество всех классов
, в качестве же множества состояний S
приведенного автомата берется множество всех классов ![]() разбиения p.
Функция переходов d
приведенного автомата А определяется следующим образом:
разбиения p.
Функция переходов d
приведенного автомата А определяется следующим образом:
т. е. значением функции переходов d
на классе разбиенияp,
содержащем некоторый элемент s, является класс разбиения, содержащий
элемент![]() , т. е. состояние, в которое переходит состояние
s автомата
, т. е. состояние, в которое переходит состояние
s автомата ![]() под действием заданного входного значения
х. (Такое задание является корректным, поскольку известно, что
эквивалентные состояния переходят в эквивалентные по любому входу х).Для
функции выходов l
полагают:
под действием заданного входного значения
х. (Такое задание является корректным, поскольку известно, что
эквивалентные состояния переходят в эквивалентные по любому входу х).Для
функции выходов l
полагают:
![]() , (2.2)
, (2.2)
т. е. значением функции выходов приведенного автомата на классе
разбиения p,
содержащем некоторый элемент s, является значение функции выходов
исходного автомата ![]() в состоянии s при том же входном значении
х. Это значение функции одно и то же для всех состояний s из
одного класса, так как все состояния в классе эквивалентны.
в состоянии s при том же входном значении
х. Это значение функции одно и то же для всех состояний s из
одного класса, так как все состояния в классе эквивалентны.
Данные о значении функции переходов и выходов заносятся в таблицу, строки которой соответствуют классам разбиения p (состояния автомата А), а столбцы – входным значениям х из Х.
Поскольку автомат Мура можно рассматривать как частный случай автомата Мили, то описанную процедуру можно использовать и для автомата Мура.
Пример 1
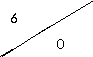
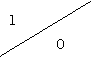
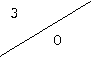
Пусть автомат Мили задан таблицей 2.13.
Построим разбиение p
по отношению неотличимости состояний. По определению разбиения ![]() в один класс должны объединяться те состояния, для
которых строки в таблице выходов (нижние треугольники клеток таблицы) совпадают.
Таким образом, имеем
в один класс должны объединяться те состояния, для
которых строки в таблице выходов (нижние треугольники клеток таблицы) совпадают.
Таким образом, имеем ![]() , где
, где ![]() ;
;![]() . Индекс вверху обозначает номер шага, на котором
отыскиваются классы. На шаге 2 методом перебора пар из классов
. Индекс вверху обозначает номер шага, на котором
отыскиваются классы. На шаге 2 методом перебора пар из классов ![]() и
и ![]() проверяем, какие из пар состояний принадлежат
одному классу
проверяем, какие из пар состояний принадлежат
одному классу ![]() . Для этого согласно определению проверяем условие
. Для этого согласно определению проверяем условие
![]() , для всех s, t из каждого
класса
, для всех s, t из каждого
класса ![]() и
и ![]() . Проверкой убеждаемся, что
. Проверкой убеждаемся, что ![]() и
и ![]()
![]() для любого x. По таблице
для любого x. По таблице ![]() ,
, ![]() в то время, как
в то время, как ![]() , а
, а ![]() . Отсюда следует, что состояния 1 и 4 должны
находиться в разных классах разбиения
. Отсюда следует, что состояния 1 и 4 должны
находиться в разных классах разбиения ![]() , а класс
, а класс ![]() таким образом расщепляется на два класса: {1, 3} и
{4}. По таблице проверкой убеждаемся, что для всех пар s, t из класса
таким образом расщепляется на два класса: {1, 3} и
{4}. По таблице проверкой убеждаемся, что для всех пар s, t из класса
![]() состояния
состояния ![]() и
и ![]() и принадлежат одному классу разбиения
и принадлежат одному классу разбиения ![]() для всех x, например
для всех x, например ![]() ,
, ![]() и
и ![]() .
.
|
0 | 1 | 2 | ||||
| 1 | 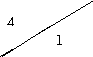
|
|
|
||||
| 2 | 
|

|
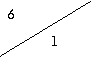
|
||||
| 3 | 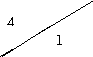
|

|
|
||||
| 4 | 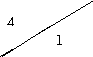
|

|

|
||||
| 5 | 
|

|

|
||||
| 6 | 
|

|
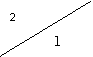
|
Таким образом, шаг 2 дает разбиение
![]() , где
, где ![]() ;
;![]() ;
; ![]() .
.
На шаге 3 перебираются пары состояний
из классов ![]() и проводится проверка переходов аналогично шагу
2.
и проводится проверка переходов аналогично шагу
2.
Шаг 3 дает разбиение ![]() .
.
Тем самым найдено разбиение по
отношению неотличимости ![]() .
.
Обозначим ![]() ;
;![]() ;
;![]() . Это и есть состояния приведенного автомата.
. Это и есть состояния приведенного автомата.
Определим теперь функцию переходов
приведенного автомата. Для этого согласно (2.1) надо найти, в какой класс
переходит каждый из классов ![]() ,
, ![]() ,
, ![]() по каждому входу 0, 1, 2.
по каждому входу 0, 1, 2.

Для функций выходов по классу ![]() согласно (2. 2) имеем:
согласно (2. 2) имеем:
![]()
![]()
![]()
Аналогично определяются значения
функций d
и l
для других классов ![]() . В итоге таблица переходов-выходов приведенного
автомата имеет вид табл. 2.14. Заменяя обозначения состояний
. В итоге таблица переходов-выходов приведенного
автомата имеет вид табл. 2.14. Заменяя обозначения состояний ![]() на более удобные обозначения i, получаем
табл. 2.15.
на более удобные обозначения i, получаем
табл. 2.15.
| 0 | 1 | 2 | |
| B1 | 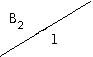
|

|
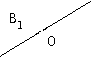
|
| B2 | 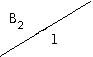
|
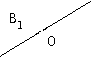
|
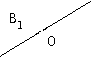
|
| B3 | 
|

|
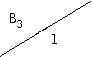
|
| 0 | 1 | 2 | |
| 1 | 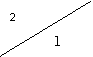
|

|

|
| 2 | 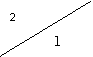
|

|

|
| 3 | 
|

|
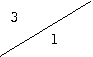
|
Пример 2
Найти минимальный автомат для автомата
![]() , заданного таблицей 2.16.
, заданного таблицей 2.16.
Найдем разбиение p:
![]() где
где ![]() ,
, ![]() .
.
| 0 | 1 | 2 | |
| 1 | 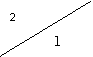
|

|

|
| 2 | 
|
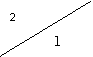
|

|
| 3 | 
|
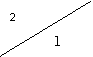
|

|
| 4 | 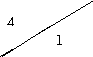
|

|
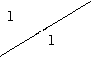
|
| 5 | 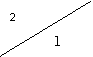
|

|

|
| 6 | 
|
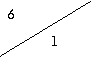
|

|
| 7 | 
|
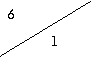
|
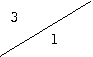
|
Для всех состояний внутри класса ![]() автомат выдает одинаковые выходные значения по
любому входу x.
автомат выдает одинаковые выходные значения по
любому входу x. ![]() где
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Пары s и t внутри классов
![]() по любому входу х переходят в пары
по любому входу х переходят в пары
![]() и
и ![]() , принадлежащие одному классу разбиения
, принадлежащие одному классу разбиения ![]() .
.
Таким образом, приведенный автомат
имеет 4 состояния: ![]() ;
;![]() ;
;![]() ;
;![]() .
.
>Определим переходы и выходы для
![]() .
.

Для функции переходов l:
![]()
![]()
![]()
Аналогично отыскиваются переходы и выходные значения для других состояний. В итоге получаем таблицу 2.17 или 2.18.
| 0 | 1 | 2 | |
| B1 | 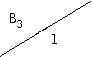
|
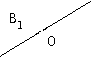
|
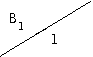
|
| B2 | 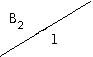
|

|
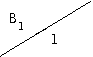
|
| B3 | 
|
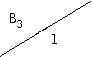
|
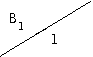
|
| B4 | 
|
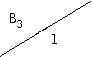
|
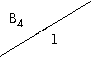
|
| 0 | 1 | 2 | |
| 1 | 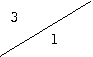
|

|
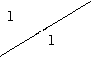
|
| 2 | 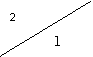
|
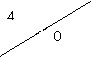
|
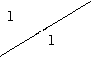
|
| 3 | 
|
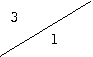
|
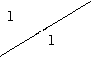
|
| 4 | 
|
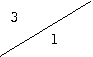
|
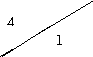
|