URL: http://cs.donntu.ru/~anoprien/Publ/1999/cogn99_7.htm

ОТ ВЫЧИСЛЕНИЙ К ПОНИМАНИЮ:
КОГНИТИВНОЕ КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
И  ОПЫТ ЕГО ПРАКТИЧЕСКОГО ПРИМЕНЕНИЯ НА ПРИМЕРЕ РЕШЕНИЯ ПРОБЛЕМЫ ФЕСТСКОГО ДИСКА

Аноприенко А. Я.
Кафедра ЭВМ ДонГТУ
anoprien@cs.donntu.ru

Abstract

Anoprienko A. A. From calculations to insight: cognitive computer simulation and its practical application on example of Phaistos Disc problem solution. The cognitive computer simulation (CCS) is fruitful synthesis of computer simulation capabilities and creative power of cognitive graphics. As an example of CCS  practical application the solution of Phaistos Disc problem is described.

"Cogito, ergo sum"
Декарт

"Информатика - это наука о
принципиально новой человеко-машинной технологии
расширенного воспроизводства качественно нового знания" [1, с.22]


 


Введение

К концу 90-х годов созрели предпосылки для качественного скачка в интенсификации познавательного использования компьютерных технологий: компьютер реально стал не только и не столько вычислительным устройством (как это, собственно, и должно было следовать из его названия), и не столько просто устройством для хранения и обработки больших объемов информации, сколько комплексным познавательным инструментом - массовым атрибутом современного образовательного процесса и научных исследований.

В связи с этим особую актуальность приобретают исследования в области изучения и анализа именно познавательных (правомерно использование и более специфического термина: когнитивных) функций компьютерных технологий. Основная цель таких исследований заключается в более глубоком понимании и, как следствие, в существенно более эффективном использовании когнитивных возможностей современного компьютера. Одним из наиболее перспективных направлений при этом является повышение когнитивной эффективности компьютерного моделирования. Краткому анализу данного направления и посвящена данная  статья. При этом вводится понятие когнитивного компьютерного моделирования (ККМ), определяемого как  синтез традиционного компьютерного моделирования и когнитивной компьютерной графики. Практическое применение  методов когнивного компьютерного моделирования иллюстрируется на примере анализа знаменитой проблемы Фестского диска.

Основные аспекты повышения когнитивной эффективности современного компьютерного моделирования

Наиболее очевидными и динамичными проявлениями качественных преобразований в современных технологиях компьютерного моделирования являются системные аспекты, спектр которых чрезвычайно широк. В контексте данной статьи остановимся лишь на тех из них, которые связаны с интенсивным развитием инфраструктуры Интернет. Формирование инфраструктуры Интернет по своей познавательной значимости соизмеримо с такими революционными событиями в распространении знаний как изобретение письменности и книгопечатания. Но в отличие от предыдущих информационных революций, нынешняя предоставляет также небывалую ранее возможность распространения динамических алгоритмизированных знаний. Другими словами, речь идет не просто о хранении и передаче данных, но о возможности практически неограниченного накопления и тиражирования информационно-программных комплексов, наиболее яркими примерами которых являются разного рода компьютерные  модели. В качестве основных тенденций развития при этом можно выделить следующие:

Особый интерес представляют  кодо-логические аспекты исследования и повышения когнитивной эффективности компьютерного моделирования, предполагающие анализ и разработки на более глубинном уровне компьютерных технологий - на уровне кодо-логического базиса [6, 7].  По сравнению с системными  влияние данных аспектов не столь очевидно и непосредственно,  но является  более фундаментальным и позволяет экстраполировать исследования на существенно более широкий исторический контекст.   В частности, это касается выявления феномена когнитивного вычислительного моделирования  (КВМ) как одного из важнейших факторов и проявлений интеллектуальной эволюции. КВМ является экстраполяцией понятия ККМ на весь спектр расширенного кодо-логического базиса и может быть определено следующим образом: плодотворный синтез числа, образа и алгоритма, позволяющий в концентрированной наглядной форме фиксировать и использовать наиболее существенные количественные и алгоритмические знания об окружающем мире. Примерами КВМ на базе монокода могут служить так называемая  Мальтинская  пластина [8] и рассматриваемый далее Фестский диск.
Для повышения когнитивной эффективности компьютерного моделирования в будущем существенным фактором представляется переход  к широкому использованию гиперлогики и гиперкодов, позволяющих эффективно учитывать и кодировать неоднозначность, неопределенность, множественность и параллельность уже на уровне элементарных числовых и логических представлений [6]. Одной из многих значимых вех на этом пути можно считать, в частности, аппаратную реализацию генератора случайных чисел в качестве стандартного архитектурного элемента  в процессорах типа Pentium III, массовое производство которых началось в 1999 году.

Непосредственно когнитивные аспекты повышения эффективности компьютерного моделирования во многих смыслах занимают как бы промежуточное положение между системными и кодо-логическими аспектами. Суть заключается в том, что аналитические и вычислительные возможности компьютерных технологий наиболее эффективно могут использоваться лишь при условии максимальной активизации интуитивно-образных возможностей человека.

Когнитивное компьютерное моделирование

Интерактивная машинная графика (ИМГ) стала уже практически обязательным атрибутом всех современных систем моделирования. Следующим шагом в данном направлении должно стать всестороннее, комплексное и целенаправленное использование ИМГ для максимальной активизации творческого и познавательного потенциала человеческого интеллекта. Разработки в данном направлении приобрели в 90-х годах особую актуальность, особенно в части когнитивно-информационной поддержки постановки и решения новых научных проблем (см., например, [10-13]).

Одним из важнейших шагов на этом пути стала разработка концепции когнитивной (т.е. способствующей познанию) компьютерной графики, основной задачей которой является "создание таких моделей представления знаний (когнитивных моделей) в которых была бы возможность однообразными средствами представлять как объекты, характерные для алгебраического мышления, так и образы-картины, с которыми оперирует геометрическое мышление" [1, с.8].

В то же время необходимо всегда учитывать, что реальные сложные системы очень часто характеризуются ярко выраженным  "контринтуитивным поведением" [14], т.е. проявления их свойств и динамики зачастую противоположны тем, которые ожидаются интуитивно. Поэтому при исследовании сложных проблем и систем полагаться  исключительно на наглядность, опыт и интуицию  нельзя. Только при условии мощной вычислительной и модельной поддержки творческий потенциал интуиции может быть использован в полной мере. И именно такой плодотворный синтез мы обозначим понятием когнитивное компьютерное моделирование.

Важнейшим атрибутом  когнитивного компьютерного моделирования являются когнитограммы, т.е. специальным образом организованная визуализация моделей, данных и результатов моделирования, ориентированная на максимальную активизацию образно-интуитивных механизмов мышления. Можно выделить три категории когнитограмм: искусственные (абстрактные), естественные (в той или иной степени имитирующие реальную или виртуальную визуальную обстановку) и комбинированные или совмещенные, объединяющие свойства первых двух категорий.

Самыми распространенными в настоящее время являются искусственные когнитограммы,  наиболее простым вариантом реализации которых можно считать использование традиционной визуализации результатов в виде разнообразных графиков и диаграмм различной размерности. Достаточно развитые возможности визуализации такого рода имеются в настоящее время как в интегрированных моделирующих системах типа Matlab, так и в электронных таблицах типа Excel. Более специфическим вариантом искусственных когнитограмм являются пифограммы, использованные в работе [1] для анализа абстрактных теоретико-числовых объектов.

Еще одним видом когнитограмм данного класса являются так называемые когнитивные карты, отображающие в виде специальных структурных схем концептуальные и логические зависимости различных когнитивных моделей. В качестве примера интенсивного использования когнитивных карт можно привести разработку программного комплекса поддержки принятия решений по управлению вузом, реализованного в объектно-ориентированной среде программирования  Smalltalk и введенного в эксплуатацию в составе информационной системы Национального технического университета Украины " Киевский политехнический институт" [15, с. 147-165].

Реализация естественных когнитограмм во  многих случаях является существенно более эффективной, чем искусственных, но требует значительных вычислительных ресурсов. Примером достаточно простого и очевидного использования естественных когнитограмм может быть имитация визуальной обстановки в исследовательских тренажерах (см., например, [16, 17]). Другим примером может быть визуализация динамики различных естественных феноменов, которые являются или могли быть объектом наблюдения, образным фоном или источником формообразующих прототипов при исследовании различных интеллектуальных процессов и артефактов интеллектуальной культуры. С исторической точки зрения наибольший интерес представляет визуализация особенностей звездного неба с учетом прецессии в соответствующую эпоху, что может иметь решающее значение при исследовании различных артефактов, подобных Фестскому диску или Мальтинской пластине. Ведь именно динамика звездного неба на протяжении тысячелетий была постоянным и наиболее значимым интеллектуальным вызовом человеческому пониманию.
Не имея возможности в рамках одной статьи детально изложить все особенности реализации и использования методов когнитивного компьютерного моделирования, ограничимся демонстрацией их практического применения на одном, достаточно показательном примере.

Решение проблемы Фестского диска

Эффективность когнитивного компьютерного моделирования наиболее наглядно может быть продемонстрирована на примере решения одной из классических научных проблем. К последним обычно относят те, которые  уже достаточно давно и широко известны научной общественности, но остаются нерешенными, несмотря  на многократные попытки их анализа и исследования традиционными методами  и средствами со стороны специалистов самого различного профиля.

К указанной категории может быть отнесена и проблема так называемого Фестского диска, обнаруженного в 1908 году во время раскопок древнекритской крепости Фест периода расцвета крито-минойской морской цивилизации (XVI  век до н.э.). Находка практически сразу же стала широко известна, и с тех пор, уже почти столетие, не прекращаются многочисленные попытки понять, чем же в действительности является это уникальное послание из далекого прошлого европейской цивилизации.

Большинство исследователей относили диск к категории письменных памятников и на этой основе предлагали самые разнообразные методы его расшифровки, ни один из которых, однако, так и не был признан достаточно убедительным. Тем не менее, описание диска, как образца еще не расшифрованной письменности, присутствует во многих фундаментальных исследованиях, посвященных истории письма (см., например, [18, с. 86-90] ).

Уже после первых неудачных попыток расшифровки Фестский диск стал своего рода символом неразрешимой загадки. Занимался, в частности, этой проблемой и знаменитый английский астроном Дж. Хокинс,  сумевший ранее с помощью ЭВМ доказать, что мегалиты Стоунхенджа являлись не только астрономической обсерваторией, но и своего рода вычислительной машиной каменного века [19]. Загадка диска ему также не поддалась, но он одним из первых достаточно четко указал на возможность не текстового, а, например, навигационного характера диска, а также - на необходимость компьютерного анализа данной проблемы [20, с. 178].


Рис.1 - Прорисовка сторон А (слева) и В (справа) Фестского диска

Побудительным мотивом к дополнительному исследованию проблемы диска автором статьи явился поиск древнейших прототипов когнитивных вычислительных моделей, основанных на монокоде. Спиральный характер узора на диске ассоциировался при этом с центральной спиралью древнесибирской мальтинской пластины, модельно-вычислительный характер которой был уже достаточно очевиден [8]. Для комплексного компьютерного анализа проблемы были использованы аналитические возможности электронных таблиц (MS Excel), моделирования  MatLab/Simulink, а также - астрономические программы, моделирующие динамику звездного  неба с учетом прецессии и обладающие наглядными и удобными средствами визуализации.

Методика исследования  сводилась к следующей последовательности действий:

1. Синтез когнитограмм, т.е. значимых когнитивных образов, имеющих отношение к проблеме, в число которых в конечном итоге были включены различные варианты графической визуализация основных количественных характеристик диска, а также - визуальные особенности звездного  неба в XVI в. до н.э.

2. Выявление на основе когнитограмм ключевых фактов, позволяющих продвинутся в понимании назначения и организации диска. Основным ключевым фактом, позволившим определить наиболее перспективное направление в расшифровке диска,  явилось особое расположение созвездия Большой Медведицы, максимально приближенной  в XVI в. до н.э. к небесному полюсу (рис. 2). При этом траектория  вращения Ковша практически точно соответствовала окружности диаметром 30 градусов, совпадающей с угловыми размерами диска на расстоянии оптимального восприятия.


Рис. 2 - Эволюция положения Большой Медведицы относительно небесного полюса


 

3. Всесторонний количественный и качественный анализ особенностей исследуемого объекта в свете обнаруженных ключевых фактов с целью генерирования и проверки гипотез относительно объекта. В частности, на рис. 3 четко просматривается нарочитая пятиричность в распределении знаков на каждой из сторон, что было бы крайне маловероятным при слоговом или иероглифическом использовании знаков для кодирования некоего связанного текста. На рис. 4 отчетливо обнаруживается разный характер распределения размеров секторов на внутренних и внешних витках спирали диска, что заставляет предположить особую значимость выравнивания размеров внешних секторов. Это позволяет сделать предположение о превалировании именно количественного подхода к размещению знаков.


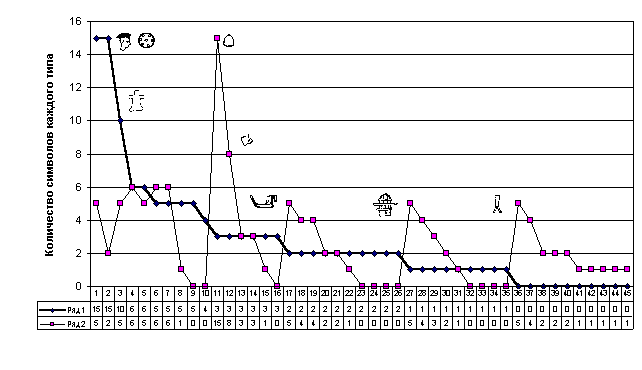
Рис. 3 - Распределение символов диска по типам: Ряд 1 - сторона А, Ряд 2 - сторона В

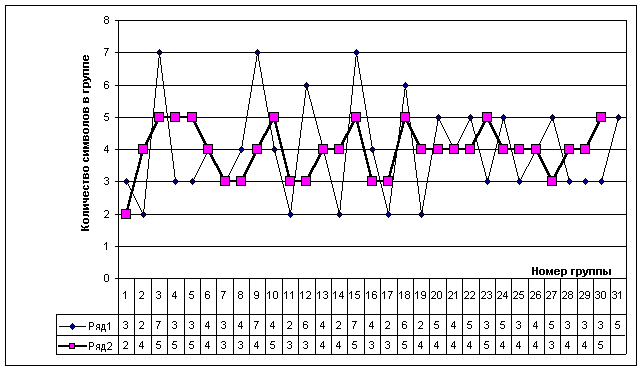
Рис. 4 - Распределение символов диска по группам: Ряд 1 - сторона А, Ряд 2 - сторона В (группы 20-31 - на внешней окружности)


 

4. Систематизация  выявленных фактов и формулируемых на их основе гипотез с параллельным анализом достоверности полученного решения.  Для эффективной реализации данного этапа была разработана и реализована концепция активных когнитивных карт или, другими словами, аргументационных схем, являющихся специальной разновидностью искусственных когнитограмм, позволяющих не только  в наглядном и компактном виде отображать всю совокупность аргументации по каждой из выдвигаемых гипотез,  но и получать для сравнительного анализа некоторые количественные оценки.  Достаточно простым и мощным средством реализации таких аргументационных схем  явилась система моделирования  MatLab/Simulink. При этом использовались следующие количественные оценки: N - аргументационный базис, характеризующий количество фактического материала (единичных независимых фактов), привлеченного для обоснования гипотезы, Pt - степень истинности гипотезы, Pf  - степень ложности гипотезы. Последние две характеристики позволяют однозначно локализовать количественную оценку достоверности гипотезы в пределах двумерного логического пространства [6]. Для оценки единичных фактов использовался дилогический базис L={1, M}, где значение 1 соответствует полностью достоверному факту (Pt =  1, Pf = 0), а М - факту, достоверность которого носит вероятностный характер, при этом принимается Pt =  Pf = 0.5. Совместное рассмотрение фактов и гипотез соответствует произведению соответствующих значений Pt и  Pf. Для реализации аргументационных схем была разработана библиотека специальных логических элементов, генерирующих перечисленную выше тройку значений  на основе комбинации как единичных фактов (T - вход значения истинности факта, F - вход значения ложности факта), так и промежуточных гипотез, характеризующихся  множеством  H={N, Pt, Pf}. Следует отметить, что на основе данного подхода возможна реализация и других вариантов реализации количественной оценки гипотез (см., например, [21] ).

На рис. 5 и 6 представлены фрагменты аргументационных схем навигационно-календарной интерпретации Фестского диска. Следует отметить, что ограничение аргументационного базиса только достоверными фактами позволяет получить полностью достоверные результаты при N=36.

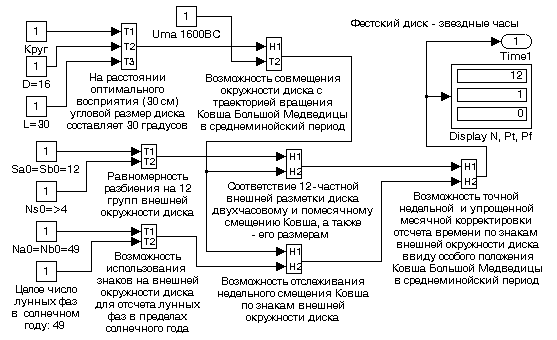
Рис. 5 - Фрагмент аргументационной схемы по проблеме Фестского диск: когнитограмма гипотезы о возможности использования диска в качестве звездных часов,  где D - диаметр диска (см), L - расстояние оптимального восприятия (см), Sa0 и Sb0 - количество секторов (групп) на внешних витках спирали сторон А и В диска, Ns0 - количество знаков в группах внешних витков спирали, Na0 и Nb0 - количество знаков на внешних витках спирали сторон А и В диска


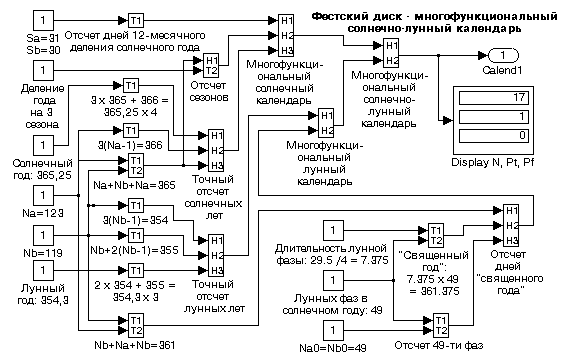
Рис. 6 - Фрагмент аргументационной схемы по проблеме Фестского диска: когнитограмма гипотезы о возможности календарного использования диска, где Na и Nb - количество знаков на сторонах A и B диска, Sa и Sb - количество групп на сторонах A и B диска

Для сравнения на рисунке 7 приведена начальная часть аргументационной схемы, составленной на основе одной из наиболее тщательно проработанных гипотез текстовой интерпретации  диска, опубликованной А.А. Молчановым в 1980 г. [22].  Через 12 лет, в 1992 году детальное обоснование данной гипотезы было опубликовано повторно и сопровождалось следующим утверждением [23, c. 156]: "Непринятие тех или иных предложенных нами слоговых чтений знаков письменности Фестского диска нисколько не поколеблет стержневой идеи нашей дешифровки, если при этом не будет доказана несостоятельность самой ее основы - методики выявления топонимов с их последующим отождествлением… Но до сих пор каких-либо возражений против данной методики со стороны специалистов не последовало." Однако, как следует из результатов выполненного автором логического моделирования данной гипотезы, опора исключительно на факты вероятностного характера приводит к катастрофически низкой степени достоверности данной гипотезы (менее 0,001) уже при N=10.


Рис. 7 - Начальный фрагмент аргументационной схемы гипотезы Молчанова, предполагающей слоговую интерпретацию знаков Фестского диска

Таким образом, на базе проведенного исследования можно уверенно утверждать, что решение проблемы Фестского диска заключается в его календарно-навигационной интерпретации. При этом, в качестве ближайшего навигационного аналога можно указать на  интенсивно использовавшийся в период европейской морской экспансии XV-XVII в. н.э. ноктурнал [24, с. 119]. Возможность выявления дополнительного смыслового содержания знаковой системы диска (например, как астрологической календарной символики или даже фрагментов некоего связного текста) при этом также не исключается, но является маловероятной и второстепенной.

Важно также отметить, что диск можно рассматривать как яркий пример весьма удачной реализации основных принципов когнитивного вычислительного моделирования. Являясь наглядным и удобным монокодовым вычислительным устройством, содержащим в концентрированном образном виде целый комплекс алгоритмизированных знаний о реальных процессах, он  не только позволял отслеживать и прогнозировать их, но и мог служить для непосредственного наблюдения  за их динамикой (реализуя своего рода интерфейс модели с реальным объектом), что  позволяло достаточно просто и эффективно решать целый комплекс довольно сложных календарно-навигационных задач и, вполне возможно, явилось одним из факторов, стимулировавших морскую экспансию крито-минойской цивилизации.

Заключение

Когнитивное компьютерное моделирование - новое перспективное научное направление, являющееся плодотворным синтезом когнитивной графики и вычислительного моделирования, позволяющее, с одной стороны, существенно повысить познавательную эффективность современных  ЭВМ, а с другой - выявить  и декодировать целый класс артефактов, относящихся к категории когнитивных вычислительных моделей на базе монокодов. К числу последних может быть отнесен и знаменитый Фестский диск, расшифровка которого может служить одним из наиболее наглядных примеров эффективного использования когнитивного компьютерного моделирования для решения трудноформализуемых научных проблем.

Литература

1. Зенкин А.А. Когнитивная компьютерная графика / Под ред. Д.А. Поспелова. - М.: Наука, Гл. ред. физ.-мат. лит., 1991. - 192 с.
2. Anoprienko A., Svjatnyi V., Braeunl T., Reuter A., Zeitz M. Massiv parallele Simulationsumgebung fuer dynamische Systeme mit konzentrierten und verteilten Parametern. Simulationstechnik./ “Simulationstechnik”, 9. Simposium in Stuttgart, Oktober 1994, Vieweg, 1994, S. 183-188
3. Гейтс Б. Дорога в будущее/Пер. с англ. - М.: Издательский отдел "Русская редакция" ТОО "Channel Trading Ltd.", 1996. - 312 c.
4. Аноприенко А. Я., Кинле А., Святный С. Н., Осипова Т. Ф. Моделирование реактора синтеза уксусной кислоты на базе моделирующей среды DIVA / В кн. “Информатика, кибернетика и вычислительная техника (ИКВТ-97). Сборник научных трудов ДонГТУ.” Выпуск 1. Донецк, ДонГТУ, 1997, с. 16-21.
5. Foster K.R. Math on the Internet. IEEE Spectrum, April 1999, p. 36-40.
6. Аноприенко А.Я. Расширенный кодо-логический базис компьютерного моделирования / В кн. “Информатика, кибернетика и вычислительная техника (ИКВТ-97). Сборник научных трудов ДонГТУ.” Выпуск 1. Донецк, ДонГТУ, 1997, с. 59-64.
7. Anoprienko A. Tetralogic and Tetracodes: an effective Method for Information Coding./ “15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics”, Berlin, August 24-29, 1997. Vol. 4. Artificial Intelligence and Computer Science. - Berlin, Wissenschaft und Technik Verl., 1997, p.751-754.
8. Anoprienko A. Interpretation of some artefacts as special simulation tools and environments / “Short Papers Proceedings of the 1997 European Simulation Multiconference ESM'97. Istanbul, June 1-4, 1997" - Istanbul, SCS, 1997, p. 23-26.
9. Пуанкаре А. О науке. - М.: Наука, 1983.
10. Палагин А.В. К проблеме проектирования системы активации научно-исследовательской деятельности / В кн. "Вопросы когнитивно-информационной поддержки постановки и решения новых научных проблем"  Сб. научн. тр./ НАН Украины. Ин-т кибернетики им. В.М.Глушкова. - Киев, 1995, с. 4-16.
11. Боюн В.П. Об одном подходе к построению системы информационно-когнитивной поддержки решения научно-исследовательских задач в компьютерной науке / В кн. "Вопросы когнитивно-информационной поддержки постановки и решения новых научных проблем"  Сб. научн. тр./ НАН Украины. Ин-т кибернетики им. В.М.Глушкова. - Киев, 1995, с. 96-102.
12. Одрин В.М. Морфологический подход к процессу постановки и решения научно-технических задач и проблем и к созданию системы когнитивно-информационной поддержки этого процесса / В кн. "Вопросы когнитивно-информационной поддержки постановки и решения новых научных проблем"  Сб. научн. тр./ НАН Украины. Ин-т кибернетики им. В.М.Глушкова. - Киев, 1995, с. 49-64
13. Шередеко Ю.Л. Психологический механизм решения задач / В кн. "Вопросы когнитивно-информационной поддержки постановки и решения новых научных проблем"  Сб. научн. тр./ НАН Украины. Ин-т кибернетики им. В.М.Глушкова. - Киев, 1995, с. 147-158.
14. Форрестер Дж. Мировая динамика: Пер. с англ. - М., Наука, 1978. - 168 с.
15. Згуровский М.З., Доброногов А.В., Померанцева Т.Н. Исследование социальных процессов на основе методологии системного анализа. - Киев: Наукова думка, 1997. - 222 с.
16. Башков Е.А., Аноприенко А.Я., Коба Ю.А., Кухтин А.А., Мальчева Р.В., Чухонцева Т.В. Система синтеза изображений в реальном времени для испытательных стендов. Гибридные вычислительные машины и комплексы, вып.15, 1992, с. 72-76.
17. Башков Е.А., Аноприенко А.Я., Сербиненко А.В., Коба Ю.А., Кухтин А.А. Из опыта разработки средств машинной графики для интенсификации учебного процесса./ “Проблемы высшей школы”. Республиканский научно-методический сборник. Выпуск 66. - Киев, Вища школа, 1988, с. 112-116.
18. Фридрих И. История письма. Пер. с нем. М.: Главная редакция восточной литературы издательства «Наука», 1979.
19. Hawkins G.S. Stonehenge decoded, Nature, 200, 306-308, 1963. (Имеется перевод: Хокинс Дж., Уайт Д. Разгадка тайны Стоунхенджа. - М.: Мир, 1973, приложение А, с. 205).
20. Хокинс Дж. Кроме Стоунхенджа, М., 1977.
21. Представление и использование знаний: Пер. с япон./ Под ред. Х.Уэно, М. Исидзука. - М.: Мир, 1989. - 220 с.
22. Молчанов А.А. Таинственные письмена первых европейцев. М.: Наука, 1980. - 119 с.
23. Молчанов А.А. Посланцы погибших цивилизаций:  Письмена древней Эгеиды. - М.: Наука, 1992.
24. Пипуныров В.Н. История часов с древнейших времен до наших дней. - М.: Наука, 1982, с. 119.

Аноприенко А.Я. От вычислений к пониманию: когнитивное компьютерное моделирование и опыт его практического применения на примере решения проблемы Фестского диска // Научные труды Донецкого государственного технического университета. Серия "Информатика, кибернетика и вычислительная техника" (ИКВТ-99). - Донецк: ДонГТУ. - 1999. - С. 36-47.
© Аноприенко А.Я.Первая инсталляция страницы: декабрь 1997 г. Основные модификации: октябрь 1999 г.