Зинченко Ю.Е.

 Проектирование генераторов псевдослучайных тестов

 

Построение на практике генератора случайной последовательности сопряжено с большими проблемами, среди которых,  прежде всего, нужно выделить следующие:

 

§        сложность создания источника случайных сигналов;

§        большие аппаратурные затраты для многоканального генератора.

 

Поэтому на практике применяют не случайные, а псевдослучайные последовательности.

К настоящему времени проектирование генераторов псевдослучайных последовательностей (ГПСТ) не представляет затруднений.

Наиболее просто строится "линейный" ГПСТ.

 

 Линейный ГПСТ и его свойства

 

Под линейным ГПСТ подразумевается генератор, который обеспечивает вероятность следования сигналов "0" и "1",  равную 0.5 или близкую к этой величине.

Среди таких генераторов на практике нашли применение генераторы на базе  р е г и с т р а   с д в и г а с  л и н е й н ы м и   о б р а т н ы м и   с в я з я м и ( РСЛОС ).

РСЛОС,  в свою очередь, это разновидность  л и н е й н о й   п о с л е д о в а т е л ь н о с т н о й  м а ш и н ы (ЛПМ ) без входов - а в т о н о м н о й   Л П М.

 

ЛПМ строится как композиция типовых компонентов, приведенных в таблице 9.1.

Для построения ГПСТ обычно применяют две эквивалентные модификации автономных ЛПМ, которые получили названия " Р С Л О С  с   в н е ш н и м и   с у м м а т о р а м и    о б р а т н ы х    с в я з е й " и " Р С Л О С   с   в н у т р е н н и м и с у м м а т о р а м и    о б р а т н ы х   с в я з е й ". Структуры указанных модификаций РСЛОС представлены на рис. 9.8 и 9.9.

 

На качество функционирования РСЛОС важнейшее влияние оказывает вид ОС, которая задается путем подбора коэффициентов g_j, j = 0,1,...,n. Ее можно описать так называемым многочленом обратной связи (МОС), который имеет следующий вид:

 

                                             (9.3)

 

где       х - фиктивная переменная многочлена;

"+" - операция "сумма по модулю 2".

 

Таблица 9.1 – Типовые компоненты РСЛОС

Наименование	Обозначение	Назначение
проводник	────────────	обеспечивает взаимосвязь элементов ЛПМ
элемент задержки		производит задержку сигнала на один такт. Для построения этого элемента может использоваться триггер, например D-типа
усилитель с коэффициентом усиления g		производит усиление сигнала в g раз, где g в общетеоретическом случае может принимать произвольное целое положительное значение, а в частном случае, что и используется на практике, принимает два значения: 0 или 1. Если g=1, то вход усилителя связывается с выходом проводником, g=0 обозначает разрыв входа с выходом или разрыв проводника
сумматор		производит суммирование по заданному модулю (обычно по "модулю 2") входных сигналов и результат выставляет на выходе

 

 

 

 

 

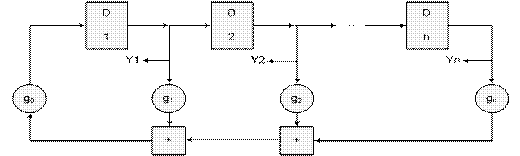
 Рис.  9.8 РСЛОС с внешними сумматорами обратных связей ( РСЛОСext ).

 

 

 

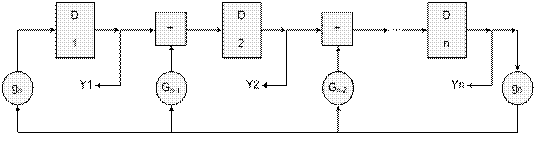
Рис. 9.9  РСЛОС с внутренними сумматорами обратных связей ( РСЛОСint ).

 

 

Доказано, что если в качестве G(X) выступает примитивный, а значит и неприводимый, многочлен, то на выходах РСЛОС генерируется периодическая последовательность с максимальным для разрядности n периодом следования сигналов, равным L = 2ⁿ - 1. Такие последовательности называются последовательностями максимальной длины или М-последовательностями.

 

Рассмотрим с в о й с т в а  М -п о с л е д о в а т е л ь н о с т е й :

 

1. С в о й с т в а п е р и о д а - период  М-последовательности, т.е. число элементов, через которые элементы повторяются, равна n

 

 L = 2ⁿ  - 1  .

 

2. С в о й с т в о к о м б и н а ц и й - М-последовательность содержит все n-значные комбинации двоичных сигналов, кроме нулевой.

 

3. С в о й с т в о  е д и н и ц   и   н у л е й - число нулевых (n0) и единичных (n1) символов М-последовательности соответственно равно :

 

n0 = 2^n-1  - 1 ;     n1 = 2^n-1 .

 

4. С в о й с т в о   с е р и й - в периоде М-последовательности из общего числа 2^n-1 серий 2^n-2 содержат один символ ( 0 или 1 ), 2^n-3  - 2 символа, 2^n-4 - 3 символа и т.д., пока 2^n-a  не станет равным 1.

 

5. С в о й с т в о  с д в и г а  и  с л о ж е н и я - сумма по "модулю 2" М-последовательности с той же самой последовательностью, что и исходная, но сдвинутая относительно первой на некоторое число t (любое число, не равное периоду) элементов, является также М-последовательностью, того же вида, что и исходная, но сдвинутая относительно нее на некоторое число элементов t` (  t` ≠ t ).

 

6. С в о й с т в о  к о р р е л я ц и и - корреляция (зависимость) элементов различных М-последовательностей M_i и M_j, а также автокорреляция элементов одной М-последовательности M_i, сдвинутых друг относительно друга на t элементов, описываются коэффициентами корреляции и автокорреляции К_ij(t), К_ai(t) соответственно, численные значения которых обратно пропорциональны периоду  М-последовательности :

 

                                                              (9.6)

 

Так как уже при небольших n коэффициенты корреляции и автокорреляции практически равны 0, появление элементов различных М-последовательностей и элементов внутри одной М-последовательности можно считать событиями практически взаимонезависимыми.

 

Анализ свойств М-последовательности показывает, что они наилучшим образом среди всевозможных последовательностей равной длины приближаются по вероятностным характеристикам к идеальной СП.

 

Описанные свойства РСЛОС позволяют считать их хорошими ГПСТ.

Учитывая к тому же простоту реализации, они являются эффективными как по функциональным возможностям, так и по аппаратурным затратам и быстродействию. Это объясняет широкое применение таких устройств, как во внешних, так и встроенных средствах псевдослучайного и компактного тестирования.

 

Недостатком описанных ГПСТ, построенных на основе РСЛОС, является то, что они способны генерировать ПСП только фиксированной вероятности следования сигналов - 0.5. Такие последовательности находят большое применение, однако там, где нужны ПСП с вероятностью отличной от 0.5, например, при желании минимизировать длину теста, нужны соответствующие ГПСТ. Построению таких генераторов посвящается следующий подраздел.

  Расчет параметров ГПСТ

 

Расчет ГПСТ, разработанный авторами данного отчета, сводится к расчету разрядности РСЛОС - n (n_j, j=1,m), а также параметров ПВ - l и g ; в качестве исходных данных при расчете выступают требуемые вероятности сигналов: Р₁,...,Р_m и соответствующие им погрешности вероятностей - E₁,...,E_m, а также допустимый коэффициент корреляции и автокорреляции - К_доп.

 

На первом этапе рассчитываются параметры l и g для всех m каналов  ГПСТ. Далеее на основе полученного множества параметров {l_j,g_j}, j=1,2,…,m, определяется разрядность одного РСЛОС, если используется ГПСТ со сосредоточенным РСЛОС, либо m РСЛОС, если используется ГПСТ с распределенным РСЛОС

 

  Расчет параметров l и g

 

Параметры l и g рассчитываются совместно, так как они одновременно влияют на вероятность выходных сигналов. Действительно, вероятность сигнала лог."1" на выходе ПВ с параметрами l и g  определяется по формуле (9.9). Эта вероятность не должна отклоняться по абсолютной величине от требуемого значения Р не более, чем допустимая погрешность Е, поэтому должно выполняться неравенство:

 

                        |  Р  - g 2^-1   | ≤ Е  .                                                      (9.10)

Разделим Р на 2^-1 - получим частное g` и остаток - r-, который назовем "отрицательным остатком":

                               Р  =  2^-1   g`  +  r-  .                                               (9.11)

 

Если в приведенное соотношение вместо g` подставить g`+1, то правая ее часть будет превышать левую на величину r+ , которую мы условно назовем "положительным остатком" :

                             r+  =  2^-1  ( g` + 1 ) - P .                                         (9.12)

 

Параметры l и g=g` либо g=g`+1 можно считать удовлетворительными, если выполняется одно из соответствующих неравенств:

                                                               r- ≤ E

или

                                                                           r+ ≤ E .

 

Отсюда следует алгоритм расчета параметров ПВ, который мы условно называем алгоритмом "LG".