Скобцов ЮЛ.* Скобцов В.Ю.**

ЭВОЛЮЦИОННЫЙ ПОДХОД К ПОСТРОЕНИЮ ТЕСТОВ ЦИФРОВЫХ СИСТЕМ

^*ДонНТУ, ул.Артема, 58, 83000, Донецк, Украина, skobtsov@kita.donntu.ru ^**ИПММ НАН Украины, ул.Р.Люксембург, 74, 83114, Донецк, Украина, skobtsov@iamm.ac.donetsk.ua

1. Генетические алгоритмы

Генетические алгоритмы (ГА), являясь одной из парадигм эволюционных вычислений, представляют собой алгоритмы случайного направленного поиска для построения (суб)оптимального решения данной проблемы, который моделирует процесс естественной эволюции. Классический “простой” ГА использует двоичные стринги для кодирования решения проблемы – особи. Это делает его привлекательным для использования в задачах генерации проверяющих тестов логических схем, где решение задачи представляется в виде двоичных наборов или их последовательностей. На множестве решений определяется целевая (fitness) функция (ЦФ), которая позволяет оценить близость каждой особи к оптимальному решению. Простой ГА использует три основных оператора: репродукция, кроссинговер-скрещивание, мутация. Используя данные операторы, популяция (множество решений данной проблемы) эволюционирует от поколения к поколению. Таким образом, чтобы задать ГА для решения конкретной проблемы, необходимо определить понятия особи, популяции, операций скрещивания и мутации, задать оценочную функцию.

2. ГА в генерации тестов

Суть задачи построения тестов заключается в поиске двоичной входной последовательности, которая для каждой неисправности из заданного множества дает различные выходные значения сигналов в исправной и неисправной схемах. На первом этапе ГА применялись для генерации тестов комбинационных ЦС [1]. Поскольку значения на выходных линиях комбинационной ЦС зависят только от значений на внешних входах и не зависят от внутреннего состояния схемы, в качестве особи выступает одиночный двоичный тестовый набор. Группа тестовых наборов образует популяцию. К выбранным таким образом особям применимы стандартные операторы кроссинговера и мутации ГА.

Поскольку целью генерации тестов является построение последовательности, на которой максимально отличаются значения сигналов в исправной и неисправной схемах, то качество тестовой последовательности (fitness-функция) оценивается как мера отличия значений сигналов в исправной и неисправной схемах. В простейшем случае для этого используются программы логического моделирования исправных цифровых схем, позволяющие оценить значения сигналов на двух соседних (во времени) тестовых наборах. На основе полученных данных моделирования разработаны fitness-функции следующего вида:

h(v, f)=c₁f₁(v, f)+c₂ * f₂(v, f),                 (2.1)

где f₁ - и f₂ - число изменений сигналов на выходах логических вентилей и триггеров соответственно ( c₂ >>c₁.)[2,3]. Целевая функция для последовательности наборов определяется как взвешенная сумма фитнесс-функций отдельных наборов

i=длина

H(s, f)= å Lⁱ *h(v_i , f),             (2.2)

i=1

где s - анализируемая последовательность; v_i - вектор из рассматриваемой последовательности, i – позиция вектора в последовательности, f - заданная неисправность, 0< L <1.

Если не удается построить тест с использованием целевой функции указанного типа, то применяются программы моделирования неисправных цифровых схем, требующие большие машинные ресурсы. Целевые функции при этом основаны на подсчете различий сигналов в исправной и неисправной схемах и имеют примерно такой же вид как и в предыдущем случае [2,3].

3. ГА в генерации тестов слабо последовательностных схем

Современные ЦС имеют сложную последовательностную структуру. Для удобства моделирования синхронная последовательностная ЦС преобразуется в псевдокомбинационный эквивалент путём обрыва обратных связей в точках их синхронизации. При генерации тестов таких ЦС с применением ГА в качестве особи используется тестовая последовательность (рис.1а). Популяция состоит из фиксированного числа тестовых последовательностей, возможно, различной длины (рис.1б). Для выбранного таким образом представления особей и популяций применяются следующие проблемно ориентированные генетические операторы[Иванов и др., 2001]:

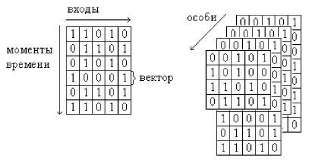
а) особь

Рис. 1. Кодирование особей и популяций в ГА.

б) популяция

Рис. 2 Операции горизонтального и вертикального скрещивания ГА.

1.     Скрещивание. Реализуется два вида операции (рис.2): вертикальное и горизонтальное скрещивания, которые выполняются соответственно с вероятностями P_v и P_h=l-P_v.

2.     Мутация. Применяются три вида операции соответственно с вероятностями Рп\ , ^п\ и ^пть, :

•     удаление одного входного вектора из случайно выбранной позиции. Применение данной операции позволяет уменьшать длину генерируемой тестовой последовательности в том случае, когда удалённый вектор не ухудшает тестовые свойства последовательности;

•      добавление одного входного вектора в случайную позицию, что также позволяет расширять область поиска решений;

•      случайная замена битов в тестовой последовательности.

4. ГА в генерации тестов сильно последовательностных схем

Обычно последовательностные схемы имеют цепи сброса (установки схемы в начальное состояние). В этом случае генерация тестов существенно упрощается и используются структурные методы генерации тестов. Для сильно последовательностных схем это условие часто не выполняется. Поэтому здесь применяется другие подходы и другие модели схемы.

Часто используется модель конечного автомата (КА). Конечный неинициальный автомат задается совокупностью пяти объектов CS,J,0,<5,^, где S - множество состояний ДУ, / - входной алфавит, О -выходной алфавит, A'.SxI^-S - функция перехода, 5\SxI^O - функция выхода. В случае верификационного подхода решение задачи поиска теста сводится, как правило, к решению проблемы распознавания заданного КА в классе неисправных КА. При этом модель неисправности не рассматривается явно. Неисправное устройство моделируется КА, отличным от данного.

Отметим, что при таком подходе часто используется модель неисправности "одиночного перехода", при которой в неисправном автомате "ломается" один переход (из одного состояния в другое). Переход между состояниями является неисправным, если выходной сигнал перехода является неправильным (1), неправильным является конечное состояние перехода (2), либо и то и другое вместе (3).

Как правило, при построении проверяющих тестов схем с памятью в этом случае используются специальные характеристические последовательности: 1) синхронизирующая; 2) установочная; 3) диагностическая; 4) уникальная [4].

Для построения этих характеристических последовательностей также используются различные методы и модели.

Чаще всего используется модель КА и последовательности строятся на основе дерева преемников [4]. Здесь также возможно использование ГА на нижнем уровне для построения характеристических последовательностей. Особи при этом представляют двоичные последовательности. При этом генетические

операторы скрещивания и мутации могут быть использованы те же (Рис.2), что применялись для построения тестов структурными методами. В качестве фитнесс-функции можно использовать функции, подсчитывающие число различаемых состояний.

При построении характеристических последовательностей могут быть использованы и структурные модели, основанные на применении многозначных моделей и алфавитов.

Таким образом, для сильно последовательностных схем целесообразно применять 2-уровневый ГА. При этом ГА первого нижнего уровня строит характеристические последовательности. Генерация этих последовательностей может быть выполнена:1)структурными методами с использованием модели в виде логической схемы; 2) на основании автоматной модели, заданной таблицей переходов и выходов.

В обоих случаях для их построения можно использовать эволюционные методы. При первом подходе характеристические последовательности генерируются с использованием многозначных моделей и фитнесс-функций, в которых подсчитывается число отличных сигналов на выходах вентилей и триггеров на основании данных логического моделирования. Во втором случае используются непосредственно таблицы переходов и выходов автоматов и фитнесс-функции, в которых подсчитывается число различаемых состояний.

Эволюционный алгоритм второго верхнего уровня при генерации тестов наряду с произвольными двоичными последовательностями использует характеристические последовательности, построенные на нижнем уровне ГА, что делает эволюционный поиск более "направленным" и повышает его эффективность.

5. Построение тестов для микропроцессорных систем

Современная технология проектирования и производства компьютерных систем позволяет реализовать в одном кристалле миллионы транзисторов. В настоящее время на одном кристалле реализуются достаточно сложные микропроцессорные системы. Их тестирование представляет очень серьезную проблему.

При построении теста МП систем необходимо иметь описание ее функционирования (включая систему команд, подробное описание каждой инструкции, способы адресации и т.п.). В настоящее время для этого используются специальные языки описания аппаратуры, например, VHDL, позволяющие получить достаточно точные модели МП систем. Рассматриваемый подход также предполагает использование описания МП системы на языке VHDL. Поскольку применяется модель МП функционального уровня, то используются функциональные неисправности этого же уровня.

Для построения тестовой последовательности МП систем на функциональном уровне используется двухуровневый ГА. Суть его заключается в следующем. Сначала выполняется анализ системы команд данной МП системы. Далее для каждой команды МП строится макрос, который представляет короткую последовательность команд, активизирующий эту команду и проверяющий правильность ее выполнения путем распространения на выходы МП одного или более результирующих машинных слов. Подобные макросы строятся для каждой команды МП системы и формируют специальную библиотеку, которая используется на следующем этапе генерации теста. Далее находятся лучшие значения параметров построенных макросов, которые обеспечивают лучшую проверку команд. Для этого используется стандартный ГА. Таким образом, на первом нижнем уровне ГА строятся подпрограммы, которые проверяют неисправности отдельных команд.

Далее они используются на втором верхнем уровне ГА для генерации полной тестовой программы. На этом уровне используется эволюционный алгоритм. Здесь популяция из N последовательностей генерируется из предыдущего поколения путем мутации. При этом применяется (N + N) стратегия – N родителей генерируют N потомков.

Для построения тестов сложных многопроцессорных вычислительных систем наиболее перспективным представляется применение методов генетического программирования. Здесь в качестве особи – решения выступает непосредсвенно программа тестирования, состоящая из операторов ассемблера. Программа описывается моделью линейного графа, для которого разработаны соответствующие генетические операторы кроссинговера и мутации.

Большая часть рассмотренные выше алгоритмов построения тестов, основанных на генетических адгоритмах, реализована в системе логического моделирования и диагностики АСМИД-Е [3].

1.    Rudnick E.M., Holm J.G., Saab D.G., Patel J.H., Application of Simple Genetic Algorithm to Sequential Circuit Test Generation // Proc. European Design & Test Conf. 1994. P.40-45.

2.    Prinetto P., Rebaudengo M., Sonza R.M. An Automatic Test Pattern Generator for Large Sequential Circuits based on Genetic Algorithms // Proc. Int. Test Conf. 1994. P.240249.

3.    Закусило С.А., Иванов Д.Е., Скобцов В.Ю., Скобцов Ю.А. Генетический подход к генерации проверяющих тестов в системе АСМИД-Е // Труды международных конференций "Искусственный интеллект" и "Интеллектуальные САПР". – М.:Физматлит.-2002. – С.49-55.

4.    Скобцов В.Ю., Скобцов Ю.А. Применение символьного моделирования при построении характеристических последовательностей // Искусственный интеллект. – 2000. - №1. – С65-72.