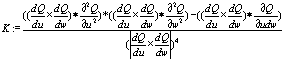 (2)
(2)поскольку на момент создания библиотеки, по запросу в поисковых стстемах "Разработка и исследование алгоритма построения квазиразвертки поверхности Е.Н.Павенко, В.Д.Фроловский" результаты были таковы:
| поисковая система | число ссылок | точность совпадения, формат документа |
|---|---|---|
| 1 | точное совпадение, *.doc | |
| Rambler | 1 | точное совпадение, *.doc |
| Yandex | 0 | - |
| Bigmir | 0 | - |
| Meta | 500 | нет совпадений, больше чем по 2 словам запроса |
Аннотация
В работе рассматривается методология решения задачи развертки поверхности с ненулевой гауссовой кривизной. Предлагаются модели и методы, которые могут использоваться в системах проектирования одежды и корпусных изделий из листового материала.
Ключевые слова: гауссова кривизна, развертывающаяся поверхность, упругие деформации
Задачи построения развертки сложных поверхностей возникают в системах конструкторско-технологической подготовки производства различных корпусных изделий из листового материала таких, как одежда, обувь, корпуса турбо-, гидрогенераторов, электрических машин, автомобилей, судов, вентиляционных систем и пр. Причем задача построения развертки может рассматриваться в двух аспектах. Во-первых, собственно построение плоской развертки сложной нелинейной поверхности, а во-вторых, задача подготовки плоской заготовки определенной формы, которая в дальнейшем, путем деформации, превращается в требуемую нелинейную поверхность.
Известные подходы к исследованию рассматриваемой задачи можно разделить на две категории: 1) геометрический, на основе методов дифференциальной геометрии [1, 4]; 2) физический, на основе теории упругопластических деформаций [3]. Однако потребности практики удовлетворены до настоящего времени не в полной мере. Наиболее целесообразным при решении прикладных задач представляется сочетание геометрических методов с учетом физических характеристик деформируемых при развертке материалов.
Отображение различных поверхностей на плоскость - типичная задача инженерной геометрии. Формулируется она следующим образом: для заданного сегмента поверхности требуется найти плоскую область такой формы, чтобы из нее путем деформации можно было бы получить исходный сегмент. Такие отображения получили название квазиразверток.
Точные развертки существуют для весьма узкого класса поверхностей. В общем случае приходится строить отображение куска поверхности на плоскую область с искажением длин или углов или того и другого.
В работе рассматривается класс параметрических поверхностей, поскольку такое описание поверхностей наиболее часто используется в настоящее время в системах автоматизированного проектирования. Общий вид такой поверхности, зависящий только от ее геометрии, то есть от расположения опорных точек, по которым строится данная поверхность, имеет вид [2]:
Q(u,w)=[U][N][P][N T][W],(1)
где [U]=[u3u3u1] и [WT]=[w3w2w1], 0<=u<=1, 0<=W<=1, N – матрица, соответствующая методу описания поверхности (бикубическая поверхность Кунса или поверхность Безье), P – матрица опорных точек, на которых строится поверхность.
>Известно, что наиболее просто строится развертка для, так называемой, развертывающейся поверхности. Если поверхность развертывающаяся, то с помощью последовательности небольших поворотов вокруг образующей линии она может быть без растяжений и разрывов развернута или раскрыта в плоскость. Для того, чтобы определить, будет ли поверхность или ее часть развертывающейся, необходимо рассмотреть гауссову кривизну этой поверхности. Для развертывающейся поверхности гауссова кривизна в любой точке поверхности равно рулю, т.е. K=0. Гауссова кривизна для поверхности в соответствии с [2] определяется как
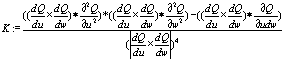 (2)
(2)
Примеры развертывающихся (конус) и неразвертывающихся поверхностей (сфера) приведены на рисунках 1 и 2.
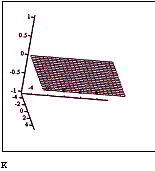
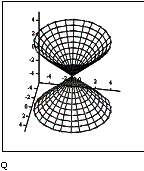
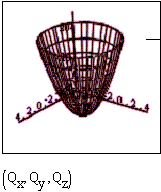
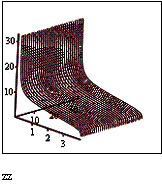
Использование значений гауссовой кривизны для возможности получения плоской развертки произвольной нелинейной поверхности может служить основой для построения алгоритма получения квазиразвертки поверхности: необходимо разбить поверхность на такие участки, в которых гауссова кривизна имеет нулевое значение. В этом случае все полученные куски поверхности являются развертывающимися, и получение для них плоских заготовок происходило бы с минимальными деформациями исходной поверхности. Исследования показали, что прямое применение данного алгоритма малоэффективно, поскольку отдельные куски поверхности для уменьшения своей гауссовой кривизны стремятся к минимальным размерам и в пределе стягиваются в точку.
Для предотвращения такой аномалии предложенного выше алгоритма предложено использовать дополнительные ограничения, связанные с подходами теории деформации и упругости, а именно- учет энергетических затрат на выполнение деформации исходной поверхности.
2.2 Метод энергетических функций
Обозначим через S - трехмерную поверхность, заданную набором трехмерных точек, N - количество точек сети по горизонтали, M - количество точек по вертикали, через Pi,j- точку трехмерной сети, стоящую на пересечении i-й горизонтали иj-й вертикали, где i=1,...,N; j=1,...,M. Каждая трехмерная точка сети
Pi,j
имеет соответственно 3 координаты:
(xi,j, yi,j, zi,j). Через
![]() -обозначим вектор, проходящий через две точки:
Pi,jи
Pk,l
.
-обозначим вектор, проходящий через две точки:
Pi,jи
Pk,l
.
Введем обобщенную функцию для углового сдвига:
![]() , где
, где
![]() ,
,
![]()
![]() ,
,
![]()
Введем функцию изгиба
![]() , где:
, где:
![]() ,
,
![]() .
.
![]()
![]()
Предположим, что наша поверхность под действием каких-либо сил был подвержена деформации, в результате которой мы получили изменение длин координатных линий и углов между ними. Обозначим через R(Pi,j, Pk,l) растяжение, а S(Pi,j, Pk,l) - сжатие сети между точками Pi,j и Pk,l . Энергии, обусловленные растяжением и сжатием соответственно обозначим через:
![]() ,
,
![]() .
.
Вид функционалов
![]() и
и
![]() выбирается исходя из конкретной энергетической модели деформаций для различных материалов.
выбирается исходя из конкретной энергетической модели деформаций для различных материалов.
Через
B(Pi,j)
- обозначим суммарный угловой сдвиг, образованный четырьмя углами в точке
![]() между вертикальными и горизонтальными линиями сети. Тогда энергия сдвига определяется как:
между вертикальными и горизонтальными линиями сети. Тогда энергия сдвига определяется как:
![]() .
.
Изгиб обозначим через:
![]() , а энергию изгиба через:
, а энергию изгиба через:
![]() .
.
В конечном итоге мы можем получить общую деформационную энергию:
![]() . (3)
. (3)
Для получения полной развертки мы можем воспользоваться несколькими подходами в зависимости от принятых предположений.