Разработка и анализ распределенных алгоритмов, Н.Санторо

Первоисточник: Design and analysis of distributed algorithms, Nicola Santoro, Carleton University, Ottawa, Canada
Перевод с английского: Шаповалов А.И.

2. Основные задачи и протоколы

Цель этой главы состоит в том, чтобы ввести некоторые из основных, базисных вычислительных задач и методов их решения. Эти задачи являются основными в том смысле, что их решение обычно (иногда часто) является необходимым для функционирования системы (например широковещание и пробуждение), они являются базовыми в смысле, что их решение часто является предварительным шагом или модулем сложных вычислений и протоколов (например, просмотр и построение связующего дерева).

Некоторые из этих задач (например, широковещание и просмотр) по их природе имеют общую сущность, другими словами эти вычислительные проблемы по определению имеют ограничение уникального инициатора (UI). Другие задачи (например пробуждение и построение связующего дерева) не имеют такого ограничения. Вычислительные различия, которые получились в связи с применением дополнительного предположения о единственном инициаторе могут быть существенными.

В эту главу мы также включили по вычислениям с многократным инициированием в древовидных сетях. Их фундаментальная важность основывается на том факте, что большинство глобальных проблем (т.е. проблем для решения которых необходимо вовлечение всех объектов) часто могут быть правильно, легко и эффективно решены проектированием протокола который будет реализован на основе связующих деревьев.

Все рассматриваемые здесь проблемы требуют для их решения ограничение возможности соединения (CN) (то есть каждый объект должен иметь возможность доступа к другому объекту). В общем случае, если не оговаривается иначе, мы также предположим полную надежность (TR) и двунаправленные связи (BL). Эти три ограничения обычно используются вместе и set R= {BL, CN, TR} называются набором стандартных ограничений.

Методики, которые вводятся в этой главе для решения вышеозначенных проблем являются базовыми. После того, как они будут должным образом поняты у вас в руках окажется мощный и необходимый комплект инструментальных средств, который может эффективно использоваться каждым разработчиком распределенных алгоритмов.

2.1. Широковещание

2.1.1. Задачи широковещания

Рассмотрим распределенную вычислительную систему, где только одному объекту х известно некоторое количество важной информации и этот объект хотел бы использовать эту информацию совместно со всеми другими объектами в системе, см. рис. 2.1.

Рисунок 2.1 – процесс широковещания

Эту задачу называют широковещанием и мы уже начали анализировать ее в предыдущей главе. Для решения этой задачи необходимо спроектировать ряд правил: что и когда должны выполнять объекты; как они будут вести себя (в пределах конечного времени) в конфигурации, где все объекты будут знать информацию; решение должно работать вне зависимости от того, какой информацией обладал объект вначале. Неотъемлемым определением задачи есть предположение, что только уникальный инициатор будет единственным объектом, который запустит задачу. Фактически это предположение вводит дополнительные ограничения, потому что уникальный инициатор должен быть объектом, содержащим начальную информацию; мы обозначим это ограничение как UI+.

Чтобы решить эту проблему, каждый объект должен быть явно вовлечен в вычисления. Следовательно для ее решения широковещательная передача требует ограничение возможности соединения (CN) (то есть каждый объект должен иметь доступ к каждому другому объекту), иначе некоторые объекты никогда не будут получать информацию. Мы видели простое решение этой проблемы – наводнения, согласно двум дополнительным ограничениям - полной надежности (TR) и двунаправленным связям (BL). Повторимся, что R= {BL, CN, TR} называются набором стандартных ограничений.

2.1.2. Цена широковещания

Как мы видели, протокол наводнения использует O(m) сообщений и в худшем случае O(d) идеальная единица измерения, где d – диаметр сети.

Первый и естественный вопрос – могут ли эти затраты быть значительно сокращены (в порядке величины) при использовании другого подхода, и если да, то на сколько. Этот вопрос эквивалентен вопросу сложности задачи широковещания. Чтобы ответить на этот тип вопросов мы должны установить нижнюю границу: найти границу f (обычно функция размера сети) и доказать, что стоимость каждого алгоритма решения является по крайней мере f. Другими словами нижняя граница необходима вне зависимости от протокола и она зависит исключительно от задачи, то есть служить индикатором того, насколько комплексна задача.

Мы обозначим как M(Bcast/RI+) и T (Bcast/RI+) сообщение и временную сложность широковещания как RI+ = R ∪ UI+ соответственно.

Нижняя граница количества идеальных временных интервалов требуемых для выполнения широковещания проста для получения. Каждый объект должен получить информацию независимо от того, насколько он отдален от инициатора, и любой объект может быть инициатором. Следовательно, в худшем случае T (Bcast/RI+) ≥ Max{d(x, y) : x, y ∈ V} = d. (2.1)

Действительно наводнение выполняет широковещание за d идеальных временных интервалов.  Это означает, что нижняя граница сжатая (то есть может быть достигнута) и что наводнение выполняется за оптимальное время. Другими словами мы знаем идеальную временную сложность широковещания.

Свойство 2.1.1. Идеальная временная сложность широковещания около RI+ is _(d). Давайте теперь рассмотрим сложность сообщения. Очевидно, нижняя граница количества сообщений также проста для вывода. В конечном счете каждый объект должен получить информацию. таким образом сообщение должно быть получено каждым из n−1 объектов, которые первоначально не имели информации.  Следовательно, M(Bcast/RI+) ≥ n −1. Приложив небольшое дополнительное усилие мы можем получить более точную нижнюю границу.

Теорема 2.1.1. M(Bcast/RI+) ≥ m.

Доказательство. Предположим, что существует корректный протокол широковещания, который при каждом выполнении использует около RI + на каждом G, то есть меньше чем  м(G) сообщений. Это означает, что есть по крайней мере одна связь в G, где ни одно сообщение не будет передано ни в одном направлении в течение выполнения алгоритма. Рассмотрим выполнение алгоритма на G и пусть e=(x, y) ∈ E будет связью, где не было передано ни одно сообщение А.  Теперь создадим новый граф G, производный от графа  G при помощи удаления ребра е, и добавляя новый узел z и два новых ребра e1 = (x, z) и e2 = (y, z) (см. рис. 2.2). Множество z находится в состоянии неинициатора. Выполним тоже же самое на новом графе G: это возможно, так как ни одно сообщение не было послано по (x, y). Но так как ни одно сообщение не посылали по ветви (x, y) в оригинальном исполнении, то x и y никогда не посылают сообщение z в текущем выполнении. В результате z никогда не будет получать информацию (то есть, изменило состояние). Это противоречит тому факту, что А является корректным протоколом широковещания.

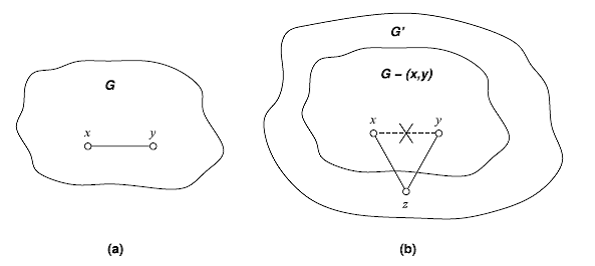
Рисунок 2.2. – Сообщение должно быть получено каждым узлом

 

Это означает, что любой алгоритм широковещания требует Q(m) сообщений.

Так как наводнение решает задачу широковещания при помощи 2m − n + 1 сообщений (см. упражнение 2.9.1), то следовательно М (Bcast/RI +) ≤ 2m − n + 1. Так как верхняя и нижняя граница имеют тот же самый порядок величины, то мы можем их суммировать.

Свойство 2.1.2. Количественная сложность широковещания около RI+ составляет Q(m).

Очевидным является то, что в плане порядка количества сообщений наводнение является оптимальным решением. Таким образом, если мы хотим спроектировать новый протокол для реализации стоимости наводнения 2m − n + 1, лучшее, что мы можем достигнуть – это уменьшить константу 2, в любом случае из-за теоремы 2.1.1. эта константа не может быть меньше 1.

2.1.3 Широковещание в  специальных сетях

В результатах, которые мы получили до настоящего времени применяются обобщенные решения, то есть решения, которые не зависят от G и таким образом могут быть  применены в независимости от топологии коммуникации (при условии, что они ненаправлены и связаны).

Следующим пунктом будет рассмотрение алгоритма выполнения широковещания в специальных сетях. Повсюду примем стандартные ограничения плюс UI+.

Широковещание в деревьях. Рассмотрим случай, когда G – дерево, то есть G – связан и не содержит циклов. В дереве m = n−1, следовательно использование протокола наводнения для выполнения широковещания в дереве будет стоить 2m − (n − 1) = 2(n − 1) − (n − 1) = n – 1 сообщений.

ВАЖНО! Эта стоимость будет достигнута, даже если объекты не знают, что сеть – дерево.

ВАЖНО! Интересным побочным эффектом выполнения широковещания в дереве является то, что дерево становится внедренным в инициатор широковещания.

Широковещание в ориентированных гиперкубах

Топологией коммуникации, которая обычно используется как сеть взаимосвязи  является k-мерный размеченный гиперкуб, обозначенный как Hk.

Ориентированный гиперкуб с количеством измерений k = 1 является парой узлов (двоичных) “0” и “1,” связанных связью и помеченных “1” в обоих узлах.

Гиперкуб Hk с количеством измерений k> 1 получен путем взятия двух гиперкубов с количеством измерений k − 1-Hk −1 и Hk−1 и соединением узлов с одинаковыми именами связью, помеченной как k в обоих узлах; имя каждого узла в Hk −1 изменяется префиксом 0 (1 соответственно), см. рисунок 2.3.

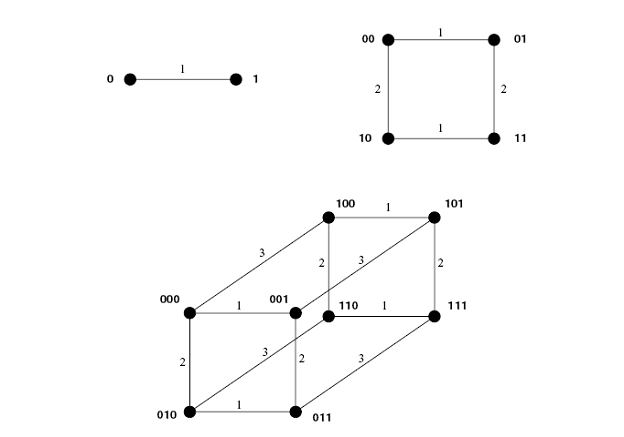
Рисунок 2.3. – Ориентированный гиперкуб

 

Так, например, узел “0010” в H 4 будет связан с узлом “0010” в H4  связью, помеченной l = 5, и их имена станут “00010” и "10010", соответственно. Эта маркировка связей является симметричной, (то есть, lx (x, y) = ly (x, y)), и называется размерным маркированием гиперкуба.

ВАЖНО! Эти имена используются только в наглядных целях, они неизвестны объектам. В отличие от этого метки связей (т.е. номера портов) известны объектам.

k-мерный гиперкуб имеет n = 2k узлов. Каждый узел имеет связи, которые промаркированы 1,2,…,к. Следовательно, общее количество связей составляет m = nk/2 = (n/2) log n = O(n log n).

Простое применение наводнения в гиперкубе будет стоить − (n − 1) = n log n − (n − 1) = n log n/2 + 1 = O(n log n) сообщений. Однако, гиперкубы являются высоко структурированными сетями с большим количеством интересных свойств. Мы можем использовать эти специальные свойства для создания более эффективного алгоритма широковещания. Очевидно, что этот протокол не сможет использоваться в других сетях.

Рассмотрим следующую базовую стратегию.

Стратегия гипернаводнения.

1.     Инициатор посылает сообщение всем его соседям.

2.     Узел получивший сообщение по маркированной связи l пошлет сообщение соседям с меткой l'<l.

ЗАМЕЧАНИЕ. Единственное различие между наводнением и гипернаводнением заключается в шаге 2: вместо того, чтобы посылать сообщение всем соседям кроме отправителя объект отправит его только некоторым из них, которыми это сообщение не было получено.

Как мы видим, эта стратегия правильно выполняет широковещание используя только n-1 сообщение (вместо O(n log n)).  Сперва исследуем корректность и завершение алгоритма.

Обозначим Hk(x) подграф Hk, определенный связями, куда алгоритмом гипернаводнения посылаются сообщения, в случае если х – инициатор. Очевидно, что каждый узел в Hk (x) получит информацию.

Лемма 2.1.1. Гипернаводнение корректно завершается.

Доказательство. Пусть х – инициатор. Начиная с  х сообщения посылаются только связям с убывающими метками и если y получит сообщение от связи 4, то  отправит его только связям 1, 2, и 3. Чтобы доказать, что каждый объект получит информацию, посланную x, мы должны показать, что для каждого узла y, есть такой путь от x до y, что последовательность меток на пути от x до y уменьшается. (Отметим, что метки на пути не должны быть последовательными целыми числами.) Для этого мы будем использовать следующее свойство гиперкубов.

Свойство 2.1.3. В к-мерном гиперкубе Hk любой узел x связан с любым другим узлом y путем π ∈ ˙[x, y] таким что _(π) – убывающая последовательность.

Доказательство. Рассмотрим названия разрядности k x и y в Hk: _xk, xk−1, . . . , x1, x0_ и _yk, yk−1, . . . , y1, y0_. Если x = y, эти две строки будут отличаться в t ≥ 1 позициях. Пусть j1, j2..., jt, - позиции в порядке убывания, то есть ji > ji+1. Рассмотрим теперь узлы v0, v1, v2, . . . , vt где v0 = x, и имя vi отличается от имени vi+1 только в ji+1-th позиции ji+1-th. Таким образом связь ji+1 соединяет vi с vi+1, и очевидно, что vt = y. Но это означает, что _v0, v1, v2, . . . , vt _ путь от x до y, и последовательность меток _j1, j2, . . . , jt _, на этом пути уменьшается.

Таком образом Hk(x) связана (то есть содержит все узлы) с Hk независимо от х. Другими словами, в пределах конечного времени каждый объект получит информацию.

Теперь сконцентрируемся на стоимости гипернаводнения. Прежде всего отметим, что M[HyperFlood/Hk] = n − 1. (2.2)

Чтобы доказать, что для осуществления широковещания необходимо n-1 сообщение, мы должны показать, что каждый объект получит информацию только один раз. Это истинно, потому что, для каждого х Hk (x) не содержит циклов (см. Упражнение 2.9.9).

Также как в упражнении, докажем, что для каждого х оригинальностью x в Hk (x) является k (см. Упражнение 2.9.10). Подразумевается, что идеальное запаздывание Гипернаводнения в Hk - всегда k. Таким образом, T[HyperFlood/Hk] = k (2.3).

Эти затраты являются наилучшими, любой алгоритм широковещания может быть выполнен в гиперкубе независимо от того, сколько данных он имеет.  Однако они получены исходя из дополнительных ограничений, что сеть – k- мерный гиперкуб с размерным маркированием, то есть H = {(G, l) = Hk}. Подводя итоги, мы имеем:

Свойство 2.1.4 Идеальная временная сложность широковещания в k-мерном гиперкубе с размерным маркированием составляет RI+ is _(k).

Свойство 2.1.5 Сложность широковещания в k-мерном гиперкубе с размерным маркированием составляет RI +  (n).

Важно! Причина, по которой мы в состоянии обойти нижнюю границу, определенную по теореме 2.1.1. является ограничение применимости протокола.

Широковещание в полных графах. Среди всех топологий сети – полный граф содержит наибольшее количество связей: каждый объект связан со всеми остальными, таким образом m = n (n − 1)/2 = O (n2) (вспомним, что мы рассматриваем двунаправленные связи) и d = 1.

Использование общего протокола потребует O (n2) сообщений. На самом деле этого не требуется.

Широковещание в полном графе может быть легко осуществлено: поскольку каждый связан с каждым, инициатор должен послать всем своим соседям (т.е. выполнить команду “send(I) to N(x)”) и широковещание завершено. В этом случае используется только n – 1 сообщение и d = 1 идеальное время.

Ясно что протокол KBcast, работает только в полном графе, который находится под дополнительным ограничением K= G полный граф. Подводя итоги:

Свойство 2.1.6. Количественная и временная сложность широковещания в полном графе RI+ is _(k), M(Bcast/RI+ ;K) = n − 1 и T (Bcast/RI+ ;K) = 1 соответственно.