Біографія

Реферат

Бібліотека

Посилання

Звіт про пошук

Індівідуальне завдання

Автореферат

по темі випускної роботи:

"Побудова MіMD-решателей рівнянь на базі

MPІ і OpenMP стандартів "

(Керівник: доцент кафедри ЕОМ Мальчева Р.В.

Консультант: асистент кафедри ЕОМ Смагин А.Н.)

Уведення. Обґрунтування актуальності теми

Моделювання динамічних систем з концентрованими і розподіленими   параметрами є актуальною проблемою для всіх областей техніки і технологій. В останні роки методи і засоби моделювання інтенсивно використовуються в реальних технічних і технологічних проектах для перевірки вірогідності проектних рішень і виступають тим самим як найважливіший фактор, що гарантує якість проектування, скорочення термінів упровадження проектів і освоєння керованих динамічних систем обслуговуючим персоналом. Граючи настільки важливу роль у технічному і технологічному прогресі, моделювання як метод дослідження висуває ряд вимог до обчислювальних систем і їх програмному забезпеченню як засобам реалізації моделей. Аналіз показує, що актуальним залишаються розробка проблемно орієнтованих рівнобіжних моделюючих середовищ (ПОПМС), у яких вазливу роль грає MіMD-решатель рівнянь. Важливою задачею є розробка рівнобіжних решателей рівнянь для динамічних мережних об'єктів з концентрованими і розподіленими параметрами. Проблемна орієнтація заключаетмя в дружньому для користувача описі об'єкта моделювання і розв'язуваних задач, у специфічному виді результатів моделювання, а також у загальному складанні інтерфейсу користувача.

Мета і задачі роботи

Метою даної роботи є розробка, налагодження й експериментальні дослідження MіMD-решателя рівнянь на базі MPІ і OpenMP стандартів, орієнтованого на рішення задач моделювання шахтних вентиляційних мереж (ШВС).

Для досягнення цієї мети в роботі зважуються такі задачі:

Характеристика мережних динамічних систем як об'єктів моделювання.

Розробка алгоритмів MіMD-решателя рівнянь на базі MPІ і OpenMP стандартів для моделі СДО з концентрованими параметрами.

Імплементація й експериментальні дослідження MІMD- решателя рівнянь на базі MPІ і OpenMP стандартів для СДО з концентрованими параметрами.

Передбачувана наукова новизна

Провести аналіз різних підходів до побудови MіMD-решателей рівнянь для моделювання мережних динамічних систем з концентрованими параметрами, що відкриває позитивні перспективи ефективного використання рівнобіжних обчислювальних ресурсів для комплексного рішення задач моделювання ШВС.

Експериментально підтвердити працездатність алгоритмів рішення рівнянь для мереж різноманітної складності.

Створити рівнобіжні решатели рівнянь, що є компоненентами рівнобіжної моделюючої середовища, що є визначеним внеском у розвиток рівнобіжних моделюючих середовищ для моделювання мережних динамічних об'єктів.

Планована практична цінність

Практична цінність роботи складається в розробці:

Працездатного й ефективного компонента рівнобіжної моделюючої середовища, MіMD-решателей рівнянь для СДО з концентрованими параметрами, що дозволяють вирішувати практичні задачі моделювання ШВС (проектної, експлуатаційні, задачі автоматизації керування);

Пакета програм мовою З++ з використанням MPІ і OpenMP, що входить до складу програмно-аппаратных засобів рівнобіжної моделюючої середовища, що може застосовуватися у вугільній промисловості й у навчальному процесі.

Що зроблено до

Основи модельного супроводу проектів ДС були значною мірою відпрацьовані на аналогових і аналого-цифрових засобах моделювання. Із середини 80-х почався інтенсивний перехід до засобів цифрового моделювання: розроблені і имплементированы на всіх типах цифрових ЕОМ блочно- і уравнение-ориентированные мови моделювання ДС, швидко розвивалася апаратна база моделювання - персональні і супер ЕОМ, рівнобіжні обчислювальні системи SІMD- і MіMD-архитектур, що була покликана компенсувати відсутність надпотужних рівнобіжних процесорів у моделюючих комплексах.

У середині 90-х була розроблена концепція розподіленої рівнобіжної моделюючої середовища ДС і структурна організація рівнобіжної моделюючої середовища, основними компонентами якої є апаратні засоби, системне і моделююче програмне забезпечення. До апаратних засобів середовища доступ можливо мати як з робочих місць, територіально наближених до надпотужних обчислювальних систем (суперSіSD, SІMD, MІMD), так і з істотно віддалених. В останньому випадку повинний використовуватися Інтернет-технологія доступу. Структурою передбачені локальні сервери, що можуть мати рівнобіжні ресурси, модельно орієнтоване периферійне устаткування і засоби побудови напівнатурних моделюючих комплексів . o:p>

Активну участь у розробці SіMD-компоненты РПМС брав участь Штутгартский університет. Спільно була розроблена структура моделюючого програмного забезпечення, досліджені рівнобіжні алгоритми моделювання ДСКП, ДСРП, розроблена підсистема діалогу, вирішений ряд тестових задач. Імплементація алгоритмів виконана на SіMD-языке рівнобіжного програмування Parallaxіs, а експериментальні дослідження - на SіMD-системе MasPar. Роботи велися в таких напрямках: узагальнення досвіду рівнобіжного моделювання на рівні мов програмування і розробка SіMD-языка моделювання у взаємозв'язку з побудовою підсистеми діалогу; дослідження аспектів объектно-ориентированного підходу; побудова бібліотек рівнобіжного моделювання ДСКП, ДСРП; експериментальні дослідження проблемно орієнтованих моделюючих SіMD-сред; застосування рівнобіжних SіMD-моделей у гірській справі і навчальному процесі. В останні роки актуальної є розробка MіMD-компоненты.

Проблема побудови РПМС є предметом наукового співробітництва факультету ВТИ з інститутом рівнобіжних і розподілених надпотужних обчислювальних систем (ІPVR) Штутгартского університету. Розробка проблемно орієнтованих середовищ виконується з інститутом системної динаміки й автоматичного керування (ІSR) Штутгартского університету і СДПП "Азот" (м. Северодонецк). Проблема інтеграції моделюючих середовищ із САПР досліджується разом з інститутом автоматизації і програмного забезпечення (ІAS) Штутгартского університету.

Поточні і плановані результати

На даний момент розроблено:

підходи до распараллеливанию алгоритмів функціонування РУ:

-         заснований на MІMD структурі,     

-         заснований на SPMD структурі.

 Пошук варіанта MІMD - распараллеливания можна вести в рамках цих програмних структур.

Процес Т₁ запускає виконання процесів. До початку можливого рівнобіжного виконання Т₁ "ведучий" процес виконує велике число послідовних операцій і підготовляє до запуску керуючі потоки Т₂ ... Т_n.

Далі ці процеси працюють паралельно і досягають кожен закінчення своєї програми і виконується операція об'єднання, що веде до синхронізації з процесом Т₁ і до терминированию потоків Т₂ ... Т_n. При кожнім виконанні рівнобіжного коду в програмі керуючі потоки генеруються і терминируются знову (рис.1.1).  .

                                                                     Рис. 1.1. 1.1. MіMD-подход до распараллеливанию

Генерування і детерминирование керуючих потоків викликає витрати ресурсів. Їхня економія досягається в SPMD - моделі распараллеливания.

 У SPMD - моделі рівнобіжні процеси (керуючі потоки) породжуються тільки один раз при запуску програми. Ці процеси терминируются наприкінці виконання програми (рис. 1.2).

 Послідовні частини програми виконуються всіма процесами, тобто мова йде про багаторазове виконання послідовних кодів програми над своїми локальними даними.
 

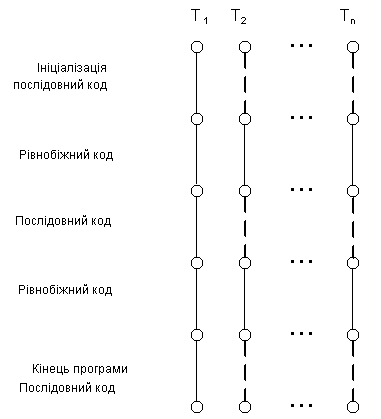
Рис. 1.2 SPMD-підхід до распараллеливанию

          Аналіз цих структур показує, що треба орієнтуватися на SPMD-організацію решателя, виконувати програму на декількох MіMD-процессорах. При цьому в кожнім процесорі будуть свої вихідні і кінцеві дані.

Аналізуючи варіанти распараллеливания операцій по обчисленню компонентів X, Y, можна запропонувати ряд варіантів віртуальної MІMD - моделі мережних об'єктів. Під віртуальною будемо розуміти модель, у якій виділені паралельно функціонуючі, відносно автономні процеси, що спільно забезпечують рішення задачі.

Схему віртуальної моделі, що распараллелена по SPMD - принципі і відповідає кількості галузей, показана на рис.1.3.

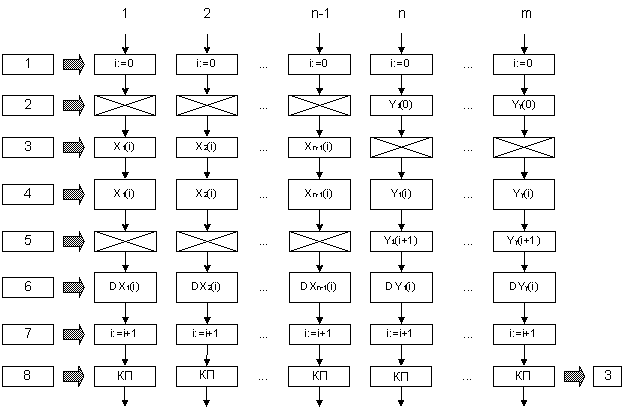
Рис. 1.3. Віртуальна MіMD-модель РУ (X і Y не об'єднані)    

У цій моделі передбачено m віртуальних процесів, кожний з який веде обчислення або компоненти X, або Y. Після перебування поточних значень компоненти X виконується обчислення значень правих частин Y компоненти, у ході якого відбувається обмін інформацією між процесами, далі елементи Y - компоненти передаються віртуальним процесам компонента X.

Девіртуалізацией назвемо процес відображення віртуальної моделі (рис. 1.4, рис. 1.5) на цільову рівнобіжну обчислювальну систему (ЦПВС), тобто ту обчислювальну систему, що є в розпорядженні користувача. Виконаємо девіртуалізацию для віртуальної моделі (рис.1.3). Як можна побачити з мал.4.5, Х - процеси простоюють частина часу, крім того, кількість операцій, що виконується цими процесами, менша, чим у Y - процесів. Їсти зміст виконати об'єднання Х - процесів у групи, що складуть X компоненту, а Y - процеси - Y компоненту, з метою вирівняти навантаження процесорів двох компонентів (рис.1.4).

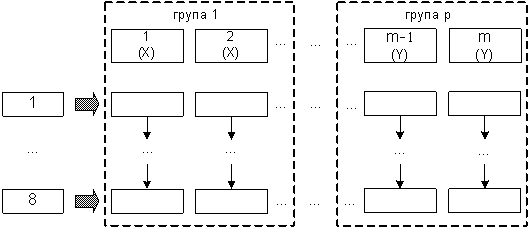
Рис. 1.4. Девіртуалізация MіMD-модели РУ (X і Y не об'єднані)

У ході подальшої роботи планується реалізувати отримані підходи за допомогою OpenMP технології і проанализироать быстродействее решателей рівнянь.

Висновок

Інтенсивний розвиток технічних засобів інформаційних технологій для моделювання складних динамічних систем надає можливості для зменшення матеріальних витрат і людських ресурсів. У ході даної роботи розробляється MіMD-решатели рівнянь на базі MPІ і OpenMP стандартів. Для того, щоб досягти поставлених перед розроблювачем цілей, необхідно розробити ефективну методику реалізації рівнобіжних решателей рівнянь з використанням ведучих MPІ і OpenMP стандартів.