Смирнов А В Сирченко Е Н Новый подход к оценке глубины экономического прогноза

Источник: Материалы III международной конференции студентов, аспирантов и молодых ученых "Компьютерный мониторинг и информационные технологии", ДонНТУ 23.05.2007
Составитель: ст. гр. ЭКИ-06(маг) Сирченко Е. Н.

НОВЫЙ ПОДХОД К ОЦЕНКЕ ГЛУБИНЫ ЭКОНОМИЧЕСКОГО ПРОГНОЗА

А. В. Смирнов
к.т.н., доцент каф. ПМиИ,
Донецкий Национальный Технический Университет
Е. Н. Сирченко
Донецкий Национальный Технический Университет

Прогнозирование временного ряда по его текущим и прошлым значениям является важной прикладной задачей. Один из наиболее распространенных методов прогнозирования заключается в экстраполяции, т.е. в продлении в будущее тенденции, наблюдавшейся в прошлом. Экстраполяция базируется на следующих допущениях:1) развитие явлении может быть с достаточным основанием охарактеризовано плавкой (эволюторной) траекторией – трендом; 2) общие условия, определяющие тенденцию развития в прошлом, не претерпят существенных изменений в будущем.

Основными требованиями, предъявляемыми к результатам прогнозирования, являются, с одной стороны, точность прогноза, а с другой – максимальная глубина прогноза. Усовершенствование существующих подходов к установлению связи глубины и точности прогноза не только с количественными, но и с качественными характеристиками базы прогнозирования является актуальным направлением для исследований.

В настоящее время в практической деятельности экономистами для оценки глубины экономического прогноза используется следующая зависимость: L+n<= , где L – период упреждения, n – количество прогнозных значений ряда, В – имеющаяся база прогноза. Такой подход для различных динамических рядов является необоснованным, поскольку никак не учитывает качественной характеристики базы прогнозирования, т.е. различную степень зашумления, уровень колеблемости, степень взаимосвязи данных исходного ряда.

Предлагается использование математического подхода к определению оптиммальной величины глубины прогноза. Для определения связи между значениями исходного ряда используется выборочная функция автокорреляции. При построении этой функции используется методика теории вероятностей для случая двух выборок. Временной лаг t характеризует сдвиг значений исходного временного ряда. На практике величина k ограничивается небольшим числом первых значений выборочной автокорреляционной функции 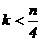. Итак, k-ый член выборочной автокорреляционной функции определяется следующим образом: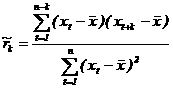. Далее необходимо найти площадь участка, находящегося под кривой функции. Найденая таким образом величина характеризует оптимальную глубину прогноза с учетом тесноты корреляционной связи между исходными данными. То есть глубина прогноза не должна превышать границ значимой связи уровней динамического ряда.

Для сравнения качества решения задач прогнозирования при традиционном и предлагаемом подходе используются доверительные интервалы прогноза для линейного тренда. В качестве примера анализа влияния качественных характеристик временных рядов на глубину прогноза были взяты три временных ряда размерностью n равной 30 с различными колеблемостями вокруг тренда. В итоге вычислений значений площади участков кривых выборочных автокорреляционных функций получились следующие оценки для оптимальной глубины прогноза: для слабоколеблемого ряда – 9 уровней, для среднеколеблемого – 3 уровня, для сильноколеблемого – 1 уровень.

При равном количестве исходных наблюдений для рядов с единым трендом и различной колеблемостью значений вокруг тренда традиционный подход предполагает возможность прогнозирования с одинаковой надежностью для периода упреждения L равного 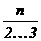. Таким образом, при таком подходе имеем оценку глубины прогноза, равную 10 - 15 уровням для каждого из временных рядов.

Доверительный интервал для оценки прогноза, сделанного в момент времени t, с упреждением L определяется следующим образом: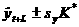, где sy – среднее квадратическое отклонение фактических наблюдений от расчетных значений y; K* = ta*K, ta - t-статистика Стьюдента, K – коэффициент, выражающий зависимость значения доверительного интервала от n и L. Зависимость K от L показывает, что влияние периода упреждения неодинаково для различных n: с ростом n влияние периода упреждения снижается. Кроме того, n влияет на величину доверительного интервала через значение статистики ta через число степеней свободы.

Анализ результатов показывает, что даже при средней колеблемости значений ряда вокруг тренда доверительный интервал оказывается весьма широким (при доверительной вероятности 90%) для периода упреждения, превышающего расчетный предлагаемым способом. Уже для упреждения на 4 уровня доверительный интервал составил почти 25% расчетного уровня. Довольно быстро экстраполяция приводит к неопределенным в статистическом смысле результатам. Это доказывает возможность применения предложенного подхода.

Поскольку выше расчет проводился основываясь на оценках величин, представляется возможным построить зависимость оценки глубины экономического прогноза от значений его базы, задав значения временного лага k и соответствующие им значения глубины экономического прогноза.

Таким образом, предложенный новый подход к оцеке глубины экономического прогноза синтезирует количественную и качественную характеристики исходных значений динамического ряда и позволяет обоснованно с математической точки зрения задавать период упреждения для экстраполируемых временных рядов.