Биография | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание
Источник: http://prognoz.org/lib/analiz-vremennykh-ryadov-boksa-dzhenkinsa (Djvu~5.1Mb)
Составитель: ст. гр. ЭКИ-06(маг) Сирченко Е. Н.
Бокс Дж. США
Дженкинс Г.М. Великобритания
Пусть 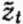 будет отклонением наблюденного ряда от любой известной детерминированной функции f(t). В частности, для стационарного ряда f(t) может быть равно среднему значению ряда
будет отклонением наблюденного ряда от любой известной детерминированной функции f(t). В частности, для стационарного ряда f(t) может быть равно среднему значению ряда 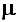 или нулю, так что
или нулю, так что 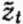 , образуют наблюденный ряд. Рассмотрим теперь общую модель АРПСС
, образуют наблюденный ряд. Рассмотрим теперь общую модель АРПСС
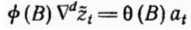

Прогноз с минимальной среднеквадратичной ошибкой. Пусть известны значения ряда до момента t. Тогда прогноз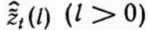 с минимальной среднеквадратичной ошибкой - это условное математическое ожидание величины
с минимальной среднеквадратичной ошибкой - это условное математическое ожидание величины 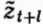 при заданных значениях
при заданных значениях 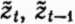
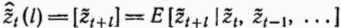
Ошибки прогноза на шаг вперед. Отсюда следует, что ошибки прогноза с упреждением, равным единице (на шаг вперед),- это не коррелированные между собой импульсы, генерируемые моделью.
Вычисление прогнозов. На практике простейший способ вычисления прогнозов - непосредственное использование разностного уравнения, а именно
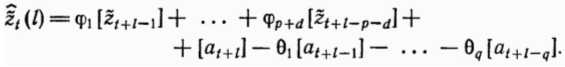
Для вычисления условных математических ожиданий в (*) вместо 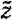 , известных к этому моменту, подставляются их значения, вместо будущих значений z - их прогноз, вместо извест ных a - их значения и вместо будущих а - нули. Процесс прогнозирования может быть начат аппроксимацией неизвестных а нулями; практически удобные представления моделей и оценки параметров получаются методами описанными в последующих главах.
, известных к этому моменту, подставляются их значения, вместо будущих значений z - их прогноз, вместо извест ных a - их значения и вместо будущих а - нули. Процесс прогнозирования может быть начат аппроксимацией неизвестных а нулями; практически удобные представления моделей и оценки параметров получаются методами описанными в последующих главах.
Вероятностные пределы для прогнозов. Их можно получить
а) вычислением вначале весов ‚ по формулам
‚ по формулам
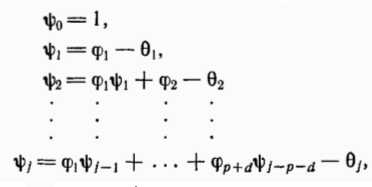
где
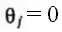 для j > q;
для j > q;
подстановкой весов
 в
в
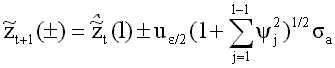
для каждого нужного уровня вероятности
 и для каждого упреждения l; здесь
и для каждого упреждения l; здесь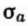 можно заменить практически его оценкой
можно заменить практически его оценкой 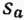 - выборочным стандартным отклонением белого шума
- выборочным стандартным отклонением белого шума  а
а  - квантиль уровня
- квантиль уровня стандартного нормального распределения.
стандартного нормального распределения.
Источник: http://prognoz.org/lib/analiz-vremennykh-ryadov-boksa-dzhenkinsa (Djvu~5.1Mb)
Составитель: ст. гр. ЭКИ-06(маг) Сирченко Е. Н.
Биография | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание