Биография | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание
Источник: http://www.iet.ru/publication.php?folder-id=44&jel-code=C53&list-page=2 (Pdf~1.3 Mb)
Составитель: ст. гр. ЭКИ-06(маг) Сирченко Е. Н.
Турунцева М.
временных рядов
Прогнозирование с использованием моделей временных рядов
является одним из наиболее простых и распространенных способов прогнозирования социально-экономических показателей. Напомним, что в данном случае под прогнозом 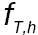 (или
(или 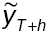 ), полученным в момент времени Т на h шагов вперед (h>0), понимается
условное математическое ожидание значения
), полученным в момент времени Т на h шагов вперед (h>0), понимается
условное математическое ожидание значения при наличии информации о данном временном ряде (и только о нем) на момент времени Т, т.е.
при наличии информации о данном временном ряде (и только о нем) на момент времени Т, т.е.
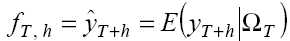
где
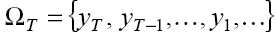 - множество всех имеющихся известных
значений временного ряда на момент времени Т.
- множество всех имеющихся известных
значений временного ряда на момент времени Т.
Прогнозы, полученные таким способом, с одной стороны, являются условно несмещенными, а с другой - обладают наименьшей среднеквадратичной ошибкой прогнозирования - MSFE (Mean Square Forecast Error) - в классе прогнозов, построенных только на основе информационного множества
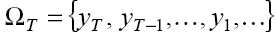 .
.
Прогнозы, полученные как условное математическое ожидание временного ряда при известных прошлых значениях этого ряда, обладают различными свойствами в зависимости от статистических характеристик временного ряда. Можно показать, что если временной ряд является стационарным в широком смысле (т.е. его безусловные математическое ожидание и дисперсия, а также ковариации различных порядков являются конечными и не зависят от времени), то прогноз, рассчитанный в момент времени Т на h шагов вперед, стремится к его безусловному математическому ожиданию при увеличении горизонта прогнозирования h, иными словами, к ситуации, когда h стремится к бесконечности. При этом дисперсия ошибки прогнозирования8 сходится к безусловной дисперсии временного ряда при h, стремящемся к бесконечности.
Аналогичными свойствами обладают прогнозы временных рядов, являющихся стационарными относительно детерминированного тренда. Различие состоит лишь в том, что в этом случае безусловное математическое ожидание не является конечным и не зависящим от времени, а прямо зависит от характеристик детерминированного тренда и, соответственно стремится к бесконечности при увеличении горизонта прогнозирования.
Таким образом, если временной ряд является стационарным в широком смысле (или стационарным относительно детерминированного тренда), то прогнозы, полученные с использованием адекватной модели временных рядов, являются устойчивыми с точки зрения сходимости последовательностей как самих прогнозов, так и их ошибок (точнее, дисперсий ошибок прогнозирования) к некоторым константам.
Если же временной ряд является интегрированным случайным процессом любого порядка, то, во-первых, прогноз для такого ряда зависит от значения временного ряда в момент прогнозирования и не имеет конечного предела при увеличении горизонта прогнозирования, а, во-вторых, дисперсия ошибки прогнозирования стремится к бесконечности при увеличении горизонта прогнозирования, т.е. в отличие от стационарного случая ошибки прогнозирования накапливаются9 при стремлении h к бесконечности. Иными словами, точность прогноза, получаемого для нестационарного временного ряда, снижается при увеличении горизонта прогнозирования.
Известно, что проблему наличия единичных корней у временных рядов можно решать несколькими способами. Применительно к вопросу о качестве получаемых прогнозов можно сказать, что предварительное тестирование рядов на наличие единичных корней и последующее построение моделей в разностях позволяют улучшить качество прогнозов.
Ещеодним способом решения проблемы наличия стохастического тренда в данных (но уже многомерных временных рядов) является оценка так называемых моделей коррекции ошибок, в которые включаются не только разности нестационарных рядов, но и (если они существуют) запаздывающие на один шаг их стационарные линейные комбинации, отражающие долгосрочные связи между переменными и с этой точки зрения являющиеся более предпочтительными по сравнению с моделями в разностях, которые отражают лишь краткосрочную динамику ряда.
Кроме того, использование моделей многомерных временных рядов может улучшить качество прогнозов и в случае, когда многомерный временной ряд является стационарным. Обоснование этой гипотезы стандартное: привлечение информации о причинных связях должно повлечь за собой улучшение качества прогнозов. Стандартные модели, которые используются в такой ситуации, - это модели векторной авторегрессии порядка p (VAR(р)).
Как и в случае одномерного временного ряда, под прогнозом 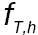 понимается условное математическое ожидание значения
понимается условное математическое ожидание значения  при
наличии информации о данном временном ряде (и только о нем)
на момент времени Т. Различие заключается в том, что в данном
случае
при
наличии информации о данном временном ряде (и только о нем)
на момент времени Т. Различие заключается в том, что в данном
случае 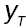 - это многомерный временной ряд.
- это многомерный временной ряд.
- Носко В., Бузаев А., Кадочников П., Пономаренко С. (2003). Анализ прогнозных свойств структурных моделей и моделей с включением результатов опросов предприятий. М.: ИЭПП. Научные труды. № 64.
- Энтов Р.М., Носко В.П., Юдин А.Д., Кадочников П.А., Пономаренко С.С. (2002). Проблемы прогнозирования некоторых макроэкономических показателей. М.: ИЭПП. Научные труды. № 46.
- Bartolomei, D.W. and Sweet, A.L. (1989). A Note on a Comparison of Exponential Smoothing Methods for Forecasting Seasonal Series //International Journal of Forecasting. № 5. P. 111-116.
- Льюис К.Д. Методы прогнозирования экономических показателей. - М.: Финансы и статистика, 1986. - 318 с.
- Chatfield, C. (1993). Calculating Interval Forecasts // Journal of Business and Economic Statistics. № 11. P. 121-135.
- Clements H. (1998). Forecasting Economic Time Series. Cambridge: Cambridge University Press. The Marshall Lectures on Economic Forecasting.
Источник: http://prognoz.org/lib/analiz-vremennykh-ryadov-boksa-dzhenkinsa (Djvu~5.1Mb)
Составитель: ст. гр. ЭКИ-06(маг) Сирченко Е. Н.
Биография | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание