Биография | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание
Источник: http://www.xplore-stat.de/tutorials/xegbohtmlnode38.html
Составитель: ст. гр. ЭКИ-06(маг) Сирченко Е. Н.
Pavel Cízek, Wolfgang Härdle, Rafa Weron
Статистические инструменты для Финансирования и страхования
4.4
Прогнозирование при помощи модели
ARIMA
4.4.1
Оптимальный прогноз
Предположим ряд ![]() соответствует общей модели
соответствует общей модели ![]() которая может быть
записана через настоящие и прошлые значения
которая может быть
записана через настоящие и прошлые значения ![]() :
:
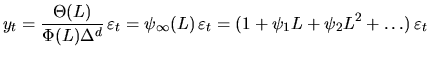 |
(4.32) |
Наша цель - предсказать будущее
значение ![]() используя нашу информационную базу,
которая состоит из прошлых значений
используя нашу информационную базу,
которая состоит из прошлых значений![]() . Будущее значение
. Будущее значение ![]() генерируемое моделью (4.32),
выражается следующим образом:
генерируемое моделью (4.32),
выражается следующим образом:![]()
Обозначим ![]()
![]() -шаг будущего прогноза
-шаг будущего прогноза![]() совершаемого на базе
совершаемого на базе ![]() . Можно показать,
что при умеренно слабых условиях,
оптимальный прогноз
. Можно показать,
что при умеренно слабых условиях,
оптимальный прогноз ![]() это условное математическое ожидание
это условное математическое ожидание![]() при заданной информационной базе,
обозначаемое
при заданной информационной базе,
обозначаемое ![]() . Условие оптимальности употребляется в
смысле минимизации среднеквадратической ошибки (СКО).
Хотя условное ожидание не должно быть линейной функцией
настоящих и прошедших значений
. Условие оптимальности употребляется в
смысле минимизации среднеквадратической ошибки (СКО).
Хотя условное ожидание не должно быть линейной функцией
настоящих и прошедших значений![]() , мы примем линейный прогноз
потому что с ним довольно легко работать. Более того,
если процесс нормальный, минимальная
ошибка среднеквадратического прогноза линейная.
Следовательно, оптимальный
, мы примем линейный прогноз
потому что с ним довольно легко работать. Более того,
если процесс нормальный, минимальная
ошибка среднеквадратического прогноза линейная.
Следовательно, оптимальный![]() -шаг будущего прогноза выглядит
следующим образом:
-шаг будущего прогноза выглядит
следующим образом:
поскольку прошлые значения
![]() -шаг будущей
прогнозной ошибки это линейная комбинация будущих шумов
поступающих в систему после момента времени
-шаг будущей
прогнозной ошибки это линейная комбинация будущих шумов
поступающих в систему после момента времени ![]() :
:
| (4.33) |
Учитывая эти результаты, если процесс
- нормальный, то интервал
прогнозирования![]() это:
это:
| (4.34) |
Для ![]() , ошибка одногошагового будущего прогноза
это
, ошибка одногошагового будущего прогноза
это ![]() , следовательно
, следовательно ![]() может быть интерпретирована
как дисперсия ошибки одношагового
будущего предсказания.
может быть интерпретирована
как дисперсия ошибки одношагового
будущего предсказания.
4.4.2
Вычисление прогнозов
Рассмотрим снова общую модель![]() которая может быть записана как:
которая может быть записана как:
| (4.35) |
где
Прогноз
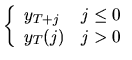 |
|||
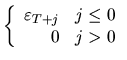 |
В практике параметры модели ![]() могут оцениваться,
но для удобства, мы примем их за данность.
могут оцениваться,
но для удобства, мы примем их за данность.
4.4.3
Возможные прогнозные функции
С учетом результатов параграфа 4.4.2,
если ряд ![]() соответствует модели
соответствует модели ![]()
![]() -шаг будущего
прогноза forecast осуществляющийся с некоторого
-шаг будущего
прогноза forecast осуществляющийся с некоторого![]() определяется из:
определяется из:
| (4.36) |
Разложим на множители полином
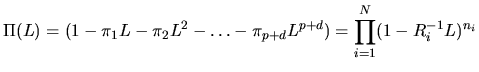 где
где ![$\displaystyle y_T(\ell) = \sum_{i=1}^{N} \left[ \sum_{j=0}^{n_i-1} k_{ij}^{T} \, \ell^j \right] (R^{-1}_i)^{\ell} \hskip 1cm \ell > q-p-d$](7/xegbohtmlimg1935.gif) |
(4.37) |
где
Выражение(4.37)называется
конечной прогнозной функцией, потому, что она охватывает
только для ![]() . Если
. Если ![]() , тогда конечная прогнозная функция
охватывает все
, тогда конечная прогнозная функция
охватывает все ![]() . Эта конечная прогнозная функция проходит
через значения
. Эта конечная прогнозная функция проходит
через значения ![]() полученные
полученные ![]() .
.
4.4.3.0.1 Пример 1. Стационарный процесс
Рассмотрим 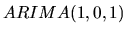 процесс со средним отклонением
процесс со средним отклонением 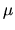 :
:
![\includegraphics[width=0.8\defpicwidth]{ar1for.ps}](7/xegbohtmlimg1948.gif)
|
Возьмем пример прогноза процесса![]() с
с ![]() and
and ![]() . Рисунок 4.12
показывает конечную прогнозную функцию
представленной модели (пунктирная линия).
Следует отметить, что эта функция
возрастает с самого начала, пока не достигнет среднего значения.
Результат этого наблюдения можно представить следующим образом:
. Рисунок 4.12
показывает конечную прогнозную функцию
представленной модели (пунктирная линия).
Следует отметить, что эта функция
возрастает с самого начала, пока не достигнет среднего значения.
Результат этого наблюдения можно представить следующим образом:
4.4.3.0.2 Пример 2 Интегрированные процессы первого порядка
Рассмотрим следующую модель ![]() :
:
Если
![]() , мы имеем модель случайного блуждания
(4.20)
и конечная прогнозная функция принимает вид:
, мы имеем модель случайного блуждания
(4.20)
и конечная прогнозная функция принимает вид:
Конечная прогнозная модель случайного блуждания со смещением (4.21) это решение следующего дифференциального уравнения:
| (4.38) |
Следовательно конечная прогнозная функция - это прямая линия, в которой только внешние помехи зависят от базы прогноза
![\includegraphics[width=0.7\defpicwidth]{rwfor.ps}](7/xegbohtmlimg1963.gif) ![\includegraphics[width=0.7\defpicwidth]{rwpdfor.ps}](7/xegbohtmlimg1964.gif)
|
IСледует отметить, что на рисунке 4.13
пределы интервалов прогноза продолжительно возрастают по
мере того, как горизонт прогноза
![]() становится больше.
Следует принять во внимание, что для нестационарных процессов
предел
становится больше.
Следует принять во внимание, что для нестационарных процессов
предел ![]() does not exist.
does not exist.
4.4.3.0.3 Пример 3. Интеграционные процессы 2-го порядка
Рассмотрим модель![]() :
:
Источник: http://www.xplore-stat.de/tutorials/xegbohtmlnode38.html
Составитель: ст. гр. ЭКИ-06(маг) Сирченко Е. Н.
Биография | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание