| назад в библиотеку |
МакКаллок и Питтс предложили использовать бинарный пороговый элемент в качестве модели искусственного нейрона. Этот математический нейрон вычисляет взвешенную сумму n входных сигналов xj, j = 1, 2... n, и формирует на выходе сигнал величины 1, если эта сумма превышает определенный порог u, и 0 - в противном случае.
Часто удобно рассматривать u как весовой коэффициент, связанный с постоянным входом x0 = 1. Положительные веса соответствуют возбуждающим связям, а отрицательные - тормозным. МакКаллок и Питтс доказали, что при соответствующим образом подобранных весах совокупность параллельно функционирующих нейронов подобного типа способна выполнять универсальные вычисления. Здесь наблюдается определенная аналогия с биологическим нейроном: передачу сигнала и взаимосвязи имитируют аксоны и дендриты, веса связей соответствуют синапсам, а пороговая функция отражает активность сомы.
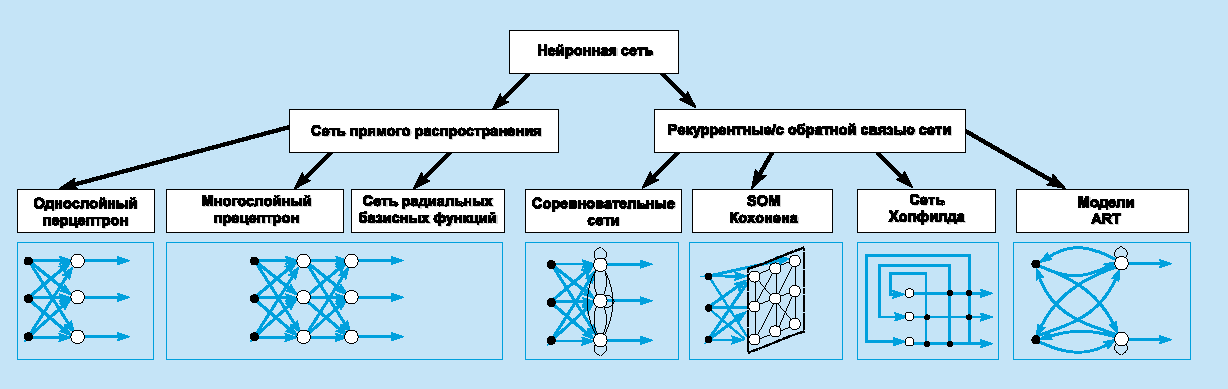
ИНС может рассматриваться как направленный граф со взвешенными связями, в котором искусственные нейроны являются узлами. По архитектуре связей ИНС могут быть сгруппированы в два класса (рис. 1): сети прямого распространения, в которых графы не имеют петель, и рекуррентные сети, или сети с обратными связями.

В наиболее распространенном семействе сетей первого класса, называемых многослойным перцептроном, нейроны расположены слоями и имеют однонаправленные связи между слоями. На рис. 1 представлены типовые сети каждого класса. Сети прямого распространения являются статическими в том смысле, что на заданный вход они вырабатывают одну совокупность выходных значений, не зависящих от предыдущего состояния сети. Рекуррентные сети являются динамическими, так как в силу обратных связей в них модифицируются входы нейронов, что приводит к изменению состояния сети.
Способность к обучению является фундаментальным свойством мозга. В контексте ИНС процесс обучения может рассматриваться как настройка архитектуры сети и весов связей для эффективного выполнения специальной задачи. Обычно нейронная сеть должна настроить веса связей по имеющейся обучающей выборке. Функционирование сети улучшается по мере итеративной настройки весовых коэффициентов. Свойство сети обучаться на примерах делает их более привлекательными по сравнению с системами, которые следуют определенной системе правил функционирования, сформулированной экспертами.
Для конструирования процесса обучения, прежде всего, необходимо иметь модель внешней среды, в которой функционирует нейронная сеть - знать доступную для сети информацию. Эта модель определяет парадигму обучения. Во-вторых, необходимо понять, как модифицировать весовые параметры сети - какие правила обучения управляют процессом настройки. Алгоритм обучения означает процедуру, в которой используются правила обучения для настройки весов.
Существуют три парадигмы обучения: "с учителем", "без учителя" (самообучение) и смешанная. В первом случае нейронная сеть располагает правильными ответами (выходами сети) на каждый входной пример. Веса настраиваются так, чтобы сеть производила ответы как можно более близкие к известным правильным ответам. Усиленный вариант обучения с учителем предполагает, что известна только критическая оценка правильности выхода нейронной сети, но не сами правильные значения выхода. Обучение без учителя не требует знания правильных ответов на каждый пример обучающей выборки. В этом случае раскрывается внутренняя структура данных или корреляции между образцами в системе данных, что позволяет распределить образцы по категориям. При смешанном обучении часть весов определяется посредством обучения с учителем, в то время как остальная получается с помощью самообучения.
Теория обучения рассматривает три фундаментальных свойства, связанных с обучением по примерам: емкость, сложность образцов и вычислительная сложность. Под емкостью понимается, сколько образцов может запомнить сеть, и какие функции и границы принятия решений могут быть на ней сформированы. Сложность образцов определяет число обучающих примеров, необходимых для достижения способности сети к обобщению. Слишком малое число примеров может вызвать "переобученность" сети, когда она хорошо функционирует на примерах обучающей выборки, но плохо - на тестовых примерах, подчиненных тому же статистическому распределению. Известны 4 основных типа правил обучения: коррекция по ошибке, машина Больцмана, правило Хебба и обучение методом соревнования.
Правило коррекции по ошибке. При обучении с учителем для каждого входного примера задан желаемый выход d. Реальный выход сети y может не совпадать с желаемым. Принцип коррекции по ошибке при обучении состоит в использовании сигнала (d-y) для модификации весов, обеспечивающей постепенное уменьшение ошибки. Обучение имеет место только в случае, когда перцептрон ошибается. Известны различные модификации этого алгоритма обучения.
Обучение Больцмана. Представляет собой стохастическое правило обучения, которое следует из информационных теоретических и термодинамических принципов. Целью обучения Больцмана является такая настройка весовых коэффициентов, при которой состояния видимых нейронов удовлетворяют желаемому распределению вероятностей. Обучение Больцмана может рассматриваться как специальный случай коррекции по ошибке, в котором под ошибкой понимается расхождение корреляций состояний в двух режимах .
Правило Хебба. Самым старым обучающим правилом является постулат обучения Хебба. Хебб опирался на следующие нейрофизиологические наблюдения: если нейроны с обеих сторон синапса активизируются одновременно и регулярно, то сила синаптической связи возрастает. Важной особенностью этого правила является то, что изменение синаптического веса зависит только от активности нейронов, которые связаны данным синапсом. Это существенно упрощает цепи обучения в реализации VLSI.
Обучение методом соревнования. В отличие от обучения Хебба, в котором множество выходных нейронов могут возбуждаться одновременно, при соревновательном обучении выходные нейроны соревнуются между собой за активизацию. Это явление известно как правило "победитель берет все". Подобное обучение имеет место в биологических нейронных сетях. Обучение посредством соревнования позволяет кластеризовать входные данные: подобные примеры группируются сетью в соответствии с корреляциями и представляются одним элементом.
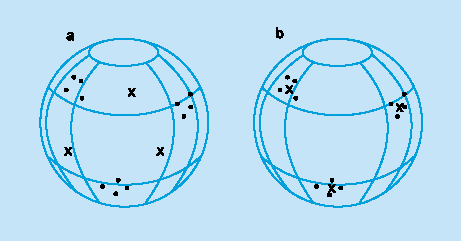
При обучении модифицируются только веса "победившего" нейрона. Эффект этого правила достигается за счет такого изменения сохраненного в сети образца (вектора весов связей победившего нейрона), при котором он становится чуть ближе ко входному примеру. На рис. 2 дана геометрическая иллюстрация обучения методом соревнования. Входные векторы нормализованы и представлены точками на поверхности сферы. Векторы весов для трех нейронов инициализированы случайными значениями. Их начальные и конечные значения после обучения отмечены Х на рис. 2а и 2б соответственно. Каждая из трех групп примеров обнаружена одним из выходных нейронов, чей весовой вектор настроился на центр тяжести обнаруженной группы.
Можно заметить, что сеть никогда не перестанет обучаться, если параметр скорости обучения не равен 0. Некоторый входной образец может активизировать другой выходной нейрон на последующих итерациях в процессе обучения. Это ставит вопрос об устойчивости обучающей системы. Система считается устойчивой, если ни один из примеров обучающей выборки не изменяет своей принадлежности к категории после конечного числа итераций обучающего процесса. Один из способов достижения стабильности состоит в постепенном уменьшении до 0 параметра скорости обучения. Однако это искусственное торможение обучения вызывает другую проблему, называемую пластичностью и связанную со способностью к адаптации к новым данным. Эти особенности обучения методом соревнования известны под названием дилеммы стабильности-пластичности Гроссберга.
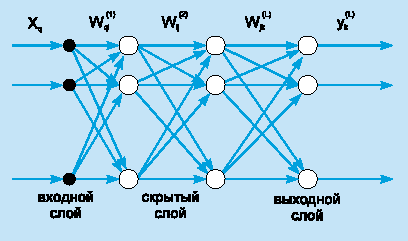
Стандартная L-слойная сеть прямого распространения состоит из слоя входных узлов (будем придерживаться утверждения, что он не включается в сеть в качестве самостоятельного слоя), (L-1) скрытых слоев и выходного слоя, соединенных последовательно в прямом направлении и не содержащих связей между элементами внутри слоя и обратных связей между слоями. На рис. 3 приведена структура трехслойной сети.
Наиболее популярный класс многослойных сетей прямого распространения образуют многослойные перцептроны, в которых каждый вычислительный элемент использует пороговую или сигмоидальную функцию активации. Многослойный перцептрон может формировать сколь угодно сложные границы принятия решения и реализовывать произвольные булевы функции [6]. Разработка алгоритма обратного распространения для определения весов в многослойном перцептроне сделала эти сети наиболее популярными у исследователей и пользователей нейронных сетей. Геометрическая интерпретация [14] объясняет роль элементов скрытых слоев (используется пороговая активационная функция).
Сети, использующие радиальные базисные функции (RBF-сети), являются частным случаем двухслойной сети прямого распространения. Каждый элемент скрытого слоя использует в качестве активационной функции радиальную базисную функцию типа гауссовой. Радиальная базисная функция (функция ядра) центрируется в точке, которая определяется весовым вектором, связанным с нейроном. Как позиция, так и ширина функции ядра должны быть обучены по выборочным образцам. Обычно ядер гораздо меньше, чем обучающих примеров. Каждый выходной элемент вычисляет линейную комбинацию этих радиальных базисных функций. С точки зрения задачи аппроксимации скрытые элементы формируют совокупность функций, которые образуют базисную систему для представления входных примеров в построенном на ней пространстве.
Существуют различные алгоритмы обучения RBF-сетей. Основной алгоритм использует двушаговую стратегию обучения, или смешанное обучение. Он оценивает позицию и ширину ядра с использованием алгоритма кластеризации "без учителя", а затем алгоритм минимизации среднеквадратической ошибки "с учителем" для определения весов связей между скрытым и выходным слоями. Поскольку выходные элементы линейны, применяется неитерационный алгоритм. После получения этого начального приближения используется градиентный спуск для уточнения параметров сети.
Этот смешанный алгоритм обучения RBF-сети сходится гораздо быстрее, чем алгоритм обратного распространения для обучения многослойных перцептронов. Однако RBF-сеть часто содержит слишком большое число скрытых элементов. Это влечет более медленное функционирование RBF-сети, чем многослойного перцептрона. Эффективность (ошибка в зависимости от размера сети) RBF-сети и многослойного перцептрона зависят от решаемой задачи.
Существует множество спорных вопросов при проектировании сетей прямого распространения - например, сколько слоев необходимы для данной задачи, сколько следует выбрать элементов в каждом слое, как сеть будет реагировать на данные, не включенные в обучающую выборку (какова способность сети к обобщению), и какой размер обучающей выборки необходим для достижения "хорошей" способности сети к обобщению.
Хотя многослойные сети прямого распространения широко применяются для классификации и аппроксимации функций, многие параметры еще должны быть определены путем проб и ошибок. Существующие теоретические результаты дают лишь слабые ориентиры для выбора этих параметров в практических приложениях.
| назад в библиотеку |