назад

Первоисточник: http://www.chipinfo.ru/literature/chipnews/200309/6.html

В. Соловьев, А. Климович

Синтез на ПЛИС многоуровневых комбинационных схем

Рассматривается метод М5 синтеза на ПЛИС многоуровневых комбинационных схем. Отмечаются положительные и отрицательные качества многоуровневых комбинационных схем, по сравнению с одноуровневыми. Метод М5 подробно описывается для универсальных PAL, а затем уточняется для "классических" PAL и CPLD. Проведенные экспериментальные исследования показали высокую эффективность метода М5, который, по сравнению с методами пакета MAX+PLUSII, позволяет для отдельных примеров снизить стоимость реализации почти в 21 раз и повысить быстродействие в 4,5 раза.

Введение

В некоторых случаях, когда требование одновременного формирования выходных сигналов комбинационной схемы не критично, можно применить методы синтеза многоуровневых комбинационных схем. Главным недостатком методов синтеза многоуровневых комбинационных схем является возможное значительное различие времени формирования значений выходных сигналов. Это связано с тем, что отдельные функции могут быть реализованы на первом уровне схемы, а некоторые - на последнем. Преимущество многоуровневых схем, по сравнению с одноуровневыми [1], заключается в меньшей стоимости реализации, измеряемой числом используемых макроячеек ПЛИС.

Отметим, что при синтезе комбинационных схем на ПЛИС для реализации промежуточных функций могут использоваться скрытые макроячейки, а для реализации межуровневых соединений - внутренние цепи обратных связей. Кроме того, при реализации многоуровневых комбинационных схем макроячейки универсальных PAL с двумя обратными связями могут одновременно использоваться для реализации промежуточных функций и приема значений входных переменных. Таким образом, при синтезе многоуровневых комбинационных схем наиболее полно используются архитектурные возможности ПЛИС.

В данной статье сохраняются обозначения работы [1]. Основные положения предлагаемого метода М5 синтеза на ПЛИС многоуровневых комбинационных схем заключаются в следующем:

Пусть Y* = {y1,...,yN,¯y1,...,¯yN} - расширенная СБФ, представляющая множество исходных функций с их инверсиями; K(ýi) - множество элементарных конъюнкций в ДНФ функции ýi, где ýi € {yi,y¯i}, i = ¯1,¯N.

Напомним, что функция ýi является подфункцией функции ýj (частью функции ýj, фактор-функцией функции ýj), если выполняется:

K(ýi)\K(ýj) = Ø, (1)

где Ø - пустое множество.

Пусть Y*(ýi) - множество функций расширенной СБФ, для которых функция ýi является подфункцией, Y*(ýi) Y*. Очевидно, что функцию ýi имеет смысл использовать в качестве подфункции функции ýj, ýj € Y*, только в том случае, когда при этом значение |K(ýj)| уменьшается по крайней мере на единицу. Поэтому эффективность использования функции ýi, ýi € Y*, в качестве подфункции функции ýj, ýj € Y*(ýi), можно выразить, при выполнении условий (1), следующим образом:

d(ýi,ýj) = |K(ýi)| – 1.

Тогда общую эффективность функции ýi, ýi € Y*, в качестве подфункции всего множества Y* можно представить в виде:

(2)

Предлагаемый подход состоит из трех этапов. На первом этапе для каждой функции yi, yi € Y, выбирается вид реализуемой функции: yi или ¯yi. На втором этапе осуществляется реализация выбранных функций и их частей, а на третьем - объединение по ИЛИ с помощью ПЛИС отдельных частей функций, реализованных на втором этапе.

Необходимым и достаточным условием реализации СБФ с помощью предлагаемого подхода является выполнение ограничений на максимальный ранг конъюнкций:

r(Ýi) <= n + k – 1, для всех i = ¯1,¯N, (3)

где r(ýi) = min(r(yi),r(¯yi)); ýi € {yi,¯yi}, i = ¯1,¯N; r(yi) и r(¯yi) - максимальный ранг (число литералов) конъюнкций в представлении yi функций и ¯yi, соответственно; при реализации на универсальных PAL k = = m + m2, при реализации на "классических" PAL k = m; m - число двунаправленных выводов PAL с одной обратной связью, m2 - число двунаправленных выводов PAL с двумя обратными связями.

При реализации СБФ на CPLD условия (3) примут вид:

r(ýi) <= n, для всех i = ¯1,¯N, (4)

где n - число входов матрицы AND функциональных блоков CPLD.

Синтез многоуровневых комбинационных схем на универсальных PAL

Пусть для реализуемой СБФ выполняются условия (3). На первом этапе для определения множества Y* реализуемых функций выполняется следующий алгоритм.

Алгоритм 1

  1. Строится расширенное представление СБФ Y* = {y1,...,yN,¯y1,...,¯yN}.
  2. Из множества Y* исключаются функции, для которых нарушено условие (3). Если условие (3) нарушено сразу для обеих функций yi и ¯yi, то реализация СБФ Y одноуровневой схемой на PAL с заданными параметрами невозможна, переход к пункту 5.
  3. Последовательно просматриваются функции множества Y*. Если функция ýi, ýi € Y*, имеет только одну форму представления (yi или ¯yi), рассматривается следующая функция. Иначе для функций yi и ¯yi, согласно (2), определяются значения D(yi) и D(¯yi) эффективности их использования в качестве подфункций для других функций. Из функций yi и ¯yi в множество Y* выбирается такая функция, для которой D(ýi) больше. В случае равенства значений D(yi) и D(¯yi) выбирается функция, для которой r(ûi) имеет наименьшее значение. В случае равенства значений r(yi) и r(¯yi) выбирается функция, для которой |K(ýj)| имеет наименьшее значение.
  4. Функция ýi, выбранная в пункте 3, сохраняется в множестве Y*, а её инверсия исключается из множества Y*.

  1. Пункты алгоритма 3 и 4 выполняются для всех i = ¯1,¯N.

  2. Конец.

Пусть множество реализуемых функций Y* представляется в виде двух матриц: троичной A и булевой B; K = {k1,...,kP} - множество различных элементарных конъюнкций в представлении функций множества Y*; X(ki) - множество аргументов, определяющих конъюнкцию ki, i = ¯1,¯P. Для каждой функции ýi, ýi € Y*, определим число С(ýi) других функций, для которых функция ýi или её часть потенциально может выступать в качестве подфункции.

Второй этап метода синтеза сводится к решению задачи 2, рассмотренной в [1]. Для решения задачи 2 из [1] используется алгоритм, аналогичный алгоритму 2 из [1], когда последовательно формируются миноры B1,...,BT, при этом покрытие некоторой единицы матрицы В на пересечении строки i и столбца j (пары (i,j)) формируемым минором BT возможно при выполнении неравенств:

|Yt {ýj}| <= k;
|Xt X(ki)| <= n + k – |Yt {ýj}|, (5)

а также, если среди свободных макроячеек t-й PAL найдется макроячейка с числом промежуточных шин qs такая, что выполняется неравенство:

Qjt + 1
qs, (6)

причем различным yj, yj € Yt, должны соответствовать различные qs, qs € Q.

Главным отличием предлагаемого подхода от алгоритма 2 из [1] является то, что если некоторая реализованная функция ýj, ýj € Y*, является подфункцией для других функций, то вводится фактор-функция wj = ýj и соответствующая промежуточная переменная gj с целью упрощения функций, для которых wj является подфункцией, а также выполняется корректировка матриц А и В в представлении исходной СБФ. В последующем каждый минор Bt будет определять реализацию функций или их частей на t-й PAL первого уровня.

С учетом сделанных замечаний, второй этап метода синтеза выполняется в соответствии со следующим алгоритмом.

Алгоритм 2

  1. Полагается t := 0.
  2. Полагается t := t + 1, Q* := Q; определяются значения K(ûj), D(ûj) и С(ýj) для всех реализуемых функций.
    Начинается формирование очередного минора BT. В качестве опорных в минор Bt включается пара (i,j) по следующим критериям:
    1) C(ýj) = max (функция ýj является подфункцией для большего числа других функций);
    2) D(ýj) = max (функция ýj наиболее эффективна в качестве подфункции);
    3) |X(ki)| = max (выбирается функция с наибольшим числом аргументов);
    4) |K(ýj)| = min (выбирается самая простая функция, тем самым создаются предпосылки для полной реализации функции ýj);

  1. Выбранные строка i и столбец j включаются в минор Bt, полагается:

    Kt := {ki};
    Xt := X(ki);
    Yt := {ýj};
    Qjt :=1.
  2. Осуществляется покрытие единиц матрицы B минором Bt. Для этого среди непокрытых единиц матрицы B отыскивается единица, для которой выполняются условия (5) и (6). При наличии альтернативы выбора пара (i,j) выбирается в соответствии со следующим порядком рассмотрения критериев:
    1) C(ýj) = max;
    2) |Xt X(ki)| = max;
    3) |X(ki) \ Xt| = min;
    4) D(ýj) = max;
    5) |K(ýj)| = min.

    Если всё ещё осталась альтернатива выбора, то предпочтение отдается единице, расположенной в столбцах минора Bt (создаются предпосылки для полной реализации функций множества Yt).

    Строка i и столбец j, на пересечении которых находится выбранная единица, включается в минор Bt, полагается:

    Kt := Kt {ki};
    Yt := Yt {ýj};
    Xt := Xt X(ki);
    Qjt := Qjt + 1.

    Если в результате включения пары (i,j) все единицы столбца j покрыты минором Bt и C(ýj) > 0, то вводится фактор-функция wj = ýj и соответствующая ей промежуточная переменная gj, а также выполняется корректировка представления СБФ.

    Пункт 3 повторяется до тех пор, пока минором Bt может быть покрыта хотя бы одна единица матрицы B.

  3. Выполняется назначение макроячеек PAL реализуемым функциям. С этой целью для каждой функции ýj, ýj € Yt, среди свободных макроячеек PAL с числом промежуточных шин, удовлетворяющих условию (6), выбирается макроячейка с минимальным значением qs. Функция ýj, ýj € Yt, назначается для реализации на s-ю макроячейку t-й PAL, полагается Q* := Q*\{qs}.
  4. Вводятся все возможные фактор-функции. Для этого последовательно просматриваются функции zj, zj € Yt, где zj - это либо функция ýj, либо её часть. Проверяется, если функция zj является подфункцией хотя бы одной ещё не реализованной функции, то вводится фактор-функция wj и соответствующая ей промежуточная переменная gj, и выполняется корректировка представления СБФ.
  5. В матрице В обнуляются единицы, покрытые минором Bt. Если в матрице B остались единицы, то выполняется переход к пункту 2; иначе выполняется переход к пункту 7.
  6. Конец.

Выполняемая в пунктах 3 и 5 корректировка представления СБФ, связанная с введением фактор-функции wj и соответствующей ей промежуточной переменной gj, заключается в следующем. Полагается P := P + 1, в матрицу A добавляется столбец, соответствующий промежуточной переменной gj. В строке P матрицы A ставится единица на пересечении с введенным столбцом. В строке P матрицы B единицы ставятся в тех столбцах, для которых функция wj является подфункцией. В этих же столбцах матрицы B обнуляются единицы, покрываемые столбцом j матрицы B. Полагается

X := X {gj};
X(kP) := {gj}.

Замечание

В общем случае, некоторая фактор-функция wj, реализуемая на t-й PAL, может использоваться для реализации других функций, которые реализуются как на t-й, так и на других PAL. При определении значения |Xt| промежуточная переменная gj не учитывается, если соответствующая ей фактор-функция wj реализуется на t-й PAL, поскольку значение gj поступает на вход матрицы AND по внутренним цепям обратных связей PAL. Если же фактор-функция wj реализуется на других PAL, то при определении значения |Xt| промежуточную переменную gj следует рассматривать как обычную входную переменную, поскольку для подачи её значения на вход t-й PAL используется внешняя цепь обратной связи.

Рассмотрим решение задачи третьего этапа. Пусть Z = {z1,...,zG} - множество промежуточных функций, представляющих собой отдельные части нереализованных функций. Выполнение третьего этапа начинается с построения булевой матрицы B, столбцы которой соответствуют выходным функциям СБФ, а строки - промежуточным функциям z1,...,zG. На пересечении строки i и столбца j матрицы B ставится единица, если функция zi является частью функции ýj. Для реализованных на первом этапе функций столбцы матрицы B будут нулевыми, и их из дальнейшего рассмотрения можно исключить. Теперь задача третьего этапа практически совпадает с задачей 2 из [1]. Поэтому для её решения может быть применен алгоритм 2 из [1].

В последующем каждый минор Bt, t = ¯1,¯T, будет определять t-ю PAL второго уровня, которая осуществляет объединение по ИЛИ не реализованных частей функций. При этом строки минора определяют входные переменные PAL, а столбцы - реализуемые функции. Необходимые значения функций на выходах всех PAL формируются путем программирования логического уровня выходного сигнала.

Пример

Пусть универсальные PAL имеют следующие параметры: n = 3, m = 2, m2 = 1 и Q = {2,2,3}. Рассмотрим синтез комбинационной схемы, заданной следующей системой логических уравнений:

y1 = x1·x2 + x2·¯x3 + x1·¯x3 + ¯x1·¯x2·x3;

y2 = ¯x4 + ¯x5·x6 + x5·¯x6;

y3 = ¯x1·¯x2·x3·¯x4·¯x5·¯x6 + ¯x1·¯x2·x3·¯x4·x5·x6 + x1·¯x2·¯x3·x4·¯x5·x6 + ¯x1·¯x2·x3·x4·x5·¯x6 + ¯x1·x2·¯x3·¯x4·¯x5·¯x6 + ¯x1·x2·¯x3·¯x4·x5·x6 + ¯x1·x2·¯x3·x4·¯x5·x6 + ¯x1·x2·¯x3·x4·x5·¯x6 + x1·¯x2·¯x3·¯x4·¯x5·¯x6 + x1·¯x2·¯x3·¯x4·x5·x6 + x1·¯x2·¯x3·x4·¯x5·x6 + x1·¯x2·¯x3·x4·x5·¯x6 + x1·x2·x3·¯x4·¯x5·¯x6 + x1·x2·x3·¯x4·x5·x6 + x1·x2·x3·x4·¯x5·x6 + x1·x2·x3·x4·x5·¯x6;

y4 = ¯x2·¯x3·¯x4·¯x5 + ¯x2·¯x3·¯x4·x6 + ¯x2·¯x3·¯x5·x6 + ¯x2·¯x3·x4·x5·¯x6 + ¯x1·x2·¯x4·¯x5 + ¯x1·x2·¯x4·x6 + ¯x1·x2·¯x5·x6 + ¯x1·x2·x4·x5·¯x6 + x1·x3·¯x4·¯x5 + x1·x3·¯x4·x6 + x1·x3·¯x5·x6 + x1·x3·x4·x5·¯x6.

Инверсные представления функций имеют вид:

¯y1 = ¯x1·¯x2·¯x3 + x1·¯x2·x3 + ¯x1·x2·x3;

¯y2 = x4·¯x5·¯x6 + x4·x5·x6;

¯y3 = ¯x1·¯x2·¯x3 + x1·¯x2·x3 + ¯x1·x2·x3 + x1·x2·¯x3 + x4·¯x5·¯x6 + ¯x4·¯x5·x6 + x4·x5·x6 + ¯x4·x5·¯x6;

¯y4 = ¯x1·¯x2·x3 + x1·x2·¯x3 + x4·¯x5·¯x6 + x4·x5·x6 + ¯x4·x5·¯x6.

Исходные данные для выполнения алгоритма 1 на первом этапе синтеза представлены в табл. 1. При выполнении пункта 2 алгоритма 1 из множества Y* исключаются функции y3 и y4, так как для них нарушено условие (3). В пункте 3 алгоритма 1 для реализации выбираются функции ¯y1 и ¯y2, так как для этих функций D(¯yi) > D(¯yi). Таким образом, в результате выполнения алгоритма 1 для реализации выбираются инверсные представления всех функций, а реализуемая СБФ показана в табл. 2.

Таблица 1. Исходные данные для работы алгоритма 1

yj y1 y2 y3 y4 y1 y2 y3 y4
D(ýj) 0 0 0 0 2 2 0 0
r(ýj) 3 2 6 6 3 3 3 3
|K(ýj)| 4 3 16 15 3 2 8 5

Таблица 2. Реализуемая система булевых функций

№ п/п Матрица A Матрица B
x1 x2 x3 x4 x5 x6 ¯y1 ¯y2 ¯y3 ¯y4
1 0 0 1 - - - 0 0 0 1
2 0 0 0 - - - 1 0 1 0
3 1 0 1 - - - 1 0 1 0
4 0 1 1 - - - 1 0 1 0
5 - - - 1 0 0 0 1 1 1
6 - - - 1 1 1 0 1 1 1
7 1 1 0 - - - 0 0 1 1
8 - - - 0 0 1 0 0 1 0
9 - - - 0 1 0 0 0 1 1

Исходные данные для работы алгоритма 2 представлены в табл. 3. В пункте 2 алгоритма 2 в минор B1 в качестве опорной включается пара (5,2), поскольку C(¯y2) = 2 = max. Затем в минор B1 добавляется единица, соответствующая паре (6,2). В результате минором B1 покрываются все единицы столбца 2. Поскольку C(¯y2) > 0 (функция ¯y2 является подфункцией для функций ¯y3 и ¯y4), то вводится фактор-функция w2 = ¯y2, соответствующая ей промежуточная переменная g2 и выполняется корректировка матриц A и B. Скорректированные матрицы A и B приведены в табл. 4. Затем в минор B1 последовательно добавляются единицы, соответствующие парам (8,3), (9,3), (10,3), (9,4) и (10,4). Больше минором B1 не может быть покрыта ни одна единица без нарушения условий (5). Система булевых функций после покрытия матрицы B минором B1 приведена в табл. 5. Аналогичным образом формируется минор B2. При этом вводится фактор-функция w1 (и соответствующая ей промежуточная переменная g1), являющаяся подфункцией для функции ¯y3. На этом второй этап синтеза заканчивается, поскольку все единицы матрицы B покрыты минорами.

Таблица 3. Исходные данные для работы алгоритма 2

ýj r(ýj) |K(ýj)| C(ýj) D(ýj)
¯y1 3 3 1 2
¯y2 3 2 2 2
¯y3 3 8 0 0
¯y4 3 5 0 0

Таблица 4. Представление системы булевых функций после реализации функции ¯y2

№ п/п Матрица A Матрица B
x1 x2 x3 x4 x5 x6 g2 ¯y1 ¯e2 ¯y3 ¯y4
1 0 0 1 - - - - 0 0 0 1
2 0 0 0 - - - - 1 0 1 0
3 1 0 1 - - - - 1 0 1 0
4 0 1 1 - - - - 1 0 1 0
5 - - - 1 0 0 - 0 1 0 0
6 - - - 1 1 1 - 0 1 0 0
7 1 1 0 - - - - 0 0 1 1
8 - - - 0 0 1 - 0 0 1 0
9 - - - 0 1 0 - 0 0 1 1
10 - - - - - - 1 0 0 1 1

Таблица 5. Представление системы булевых функций после покрытия матрицы В минором B1

№ п/п Матрица A Матрица B
x1 x2 x3 x4 x5 x6 g2 ¯y1 ¯e2 ¯y3 ¯y4
1 0 0 1 - - - - 0 0 0 1
2 0 0 0 - - - - 1 0 1 0
3 1 0 1 - - - - 1 0 1 0
4 0 1 1 - - - - 1 0 1 0
5 - - - 1 0 0 - 0 0 0 0
6 - - - 1 1 1 - 0 0 0 0
7 1 1 0 - - - - 0 0 1 1
8 - - - 0 0 1 - 0 0 0 0
9 - - - 0 1 0 - 0 0 0 0
10 - - - - - - 1 0 0 0 0

На третьем этапе синтеза в схему вводится одна дополнительная PAL, на входы которой подаются значения реализованных частей функций ¯y3 и ¯y4, а на выходах формируются функции y3 и y4. Прямые значения всех функций образуются путем программирования логического уровня выходных сигналов. В итоге логические уравнения реализуемых функций выглядят следующим образом:

y1 = ¯w1 = !(¯x1·¯x2·¯x3 + x1·¯x2·x3 + ¯x1·x2·x3);
y2 = ¯w2 = !(x4·¯x5·x6 + x4·x5·x6);
¯y3-1 = w2 + ¯x4·¯x5·x6 + ¯x4·x5·¯x6;
¯y3-2 = w1 + x1·x2·¯x3;
y3 = !(¯y3-1 + ¯y3-2);
¯4-1 = w2 + ¯x4·x5·¯x6;
¯y4-2 = ¯x1·¯x2·x3 + x1·x2·¯x3;
y4 = !(¯y4-1 + ¯y4-2).

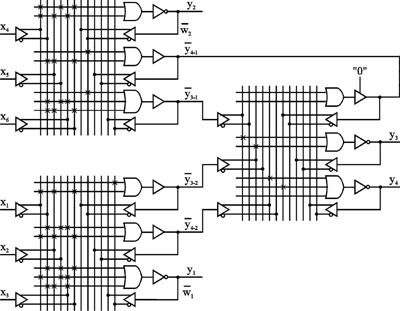
Окончательная реализация комбинационной схемы показана на рисунке.

Рисунок . Реализация СБФ многоуровневой схемой на универсальных PAL

Синтез многоуровневых комбинационных схем на "классических" PAL Поскольку "классические" PAL не по- зволяют программировать логический уровень выходных сигналов, то при синтезе комбинационных схем с использованием внутренних цепей обратных связей ПЛИС в качестве множества Y* реализуемых функций выбирается одно из множеств Y = {y1,...,yN} или Y = = {y1,...,yN}. Если в неравенствах (5) принять k = m + b, где m - число двунаправленных, в b - комбинационных выходов "классических" PAL, то рассмотренный выше метод синтеза комбинационных схем с использованием внутренних цепей обратных связей ПЛИС на универсальных PAL может быть применен и для синтеза комбинационных схем на "классических" PAL.

Синтез многоуровневых комбинационных схем на CPLD

Необходимым и достаточным условием применения метода синтеза комбинационных схем с использованием внутренних цепей обратных связей CPLD является выполнение неравенств (4). Первый этап метода синтеза выполняется точно так же, как при синтезе комбинационных схем на универсальных PAL. На втором этапе задача сводится к покрытию матрицы B минимальным числом T миноров B1,...,BT таким образом, чтобы для каждого минора выполнялись условия:

|Yt| <= m;
|Xt| <= n, (7)
Qt <= q, для всех t = ¯1,¯T,

где Qt= jQtj;

а также для каждого столбца j минора Bt выполнялось

Qjt <= qmax, (8)

где m - число выходных макроячеек CPLD; Yt - множество функций, соответствующих столбцам минора Bt; Xt - множество аргументов, соответствующих строкам минора Bt,

Kt - множество конъюнкций, соответствующих строкам минора Bt; Qjt - число единиц в столбце j минора Qt, t = ¯1,¯T. Каждый минор Qt определяет подмножество выходных функций или их частей, реализуемых на одном функциональном блоке CPLD.

При построении очередного минора Qt, t = ¯1,¯T, некоторая единица матрицы B на пересечении строки i и столбца j может быть покрыта минором Qt при выполнении неравенств:

|Yt {yj}| <= m;
|Xt X(ki)| <= n, (9)
Qt + 1 <= q,

а также, если выполняется неравенство:

Qjt + 1 <= qmax. (10)

Второй этап синтеза комбинационных схем на CPLD с использованием внутренних цепей обратных связей совпадает с алгоритмом 2, за исключением того, что в вместо условий (5) и (6) рассматриваются соответственно условия (9) и (10).

Третий этап синтеза выполняется аналогично третьему этапу синтеза для универсальных PAL.

Результаты экспериментальных исследований

Метод М5 синтеза многоуровневых комбинационных схем реализован программно в пакете ZUBR. Экспериментальные исследования проводились для сравнения метода М5 с методом пакета MAX+PLUSII версии 10.1 фирмы Altera. В качестве ПЛИС рассматривались универсальные PAL семейства CLASSIC.

Анализ полученных результатов (табл. 6) показывает, что метод М5, по сравнению с методами пакета MAX+PLUSII, при синтезе комбинационных схем на ПЛИС семейства CLASSIC позволяет значительно снизить стоимость реализации (в среднем, в 6,14 раза, а для отдельных примеров - в 20,91 раза) и повысить быстродействие (в среднем, в 1,43 раза, а для отдельных примеров - в 4,53 раза).

Таблица 6. Результаты сравнения метода М5 с методом пакета MAX+PLUSII для семейства CLASSIC

Name L N P CA C5 CA/C5 DA D5 DA/D5
9sym 9 1 87 27 11 2,45 44 60 0,73
Alu4 14 8 1028 554 75 7,39 270 140 1,93
Apex1 45 45 206 (1) 110 - (1) 80 -
Apex2 39 3 1035 (1) 49 - (1) 80 -
Apex3 54 50 280 333 119 2,80 108 100 1,08
Apex4 9 19 438 564 155 1,64 106 100 1,06
B12 15 9 431 9 9 1,00 20 20 1,00
Cps 24 109 654 235 14 16,79 44 100 0,44
Ex1010 10 10 1024 770 78 9,87 304 80 3,8
Inc 7 9 34 14 11 1,27 32 40 0,8
Pdc 16 40 1280 (1) 72 - (1) 60 -
Seq 41 35 1459 407 117 3,49 122 180 0,68
Table3 14 14 175 114 55 2,07 54 100 0,54
Table5 17 15 158 101 50 2,02 42 80 0,53
Z9sym 9 1 420 230 11 20,91 272 60 4,53
        936 73,7   1280 17,12
mid         62,4 6,14   85,33 4,43

Литература

  1. Соловьев В.В., Климович А. Синтез на ПЛИС одноуровневых комбинационных схем // ChipNews. 2003. № 6. С. 20–27.