Анализ структуры непроизводительного времени для ГПС механической обработки, проведенный как авторами статьи, так и другими специалистами [1, 2 и др.], показал, что наиболее существенными составляющими потерь времени являются: время, затрачиваемое на операциях переналадок отдельных ГПМ при поступлении партии деталей другого наименования на операцию, выполняемую данным ГПМ [так называемой партияоперации (ПО)]; время, затрачиваемое на транспортирование партий деталей к ГПМ; время простоев ГПМ из-за ожидания конца обработки ПО на предыдущей операции, осуществляемой на другом ГПМ.
В большинстве случаев, связанных с сокращением доли непроизводительного времени в расписании ГПС, затраты времени на переналадку ГПМ принимают как известные (рассчитанные ранее к моменту составления расписания посредством матриц временных затрат на переналадку [3 и 4]). Подобный подход, упрощающий процедуру определения времени переналадок ГПМ, приемлем для не полностью автоматизированных производств. В условиях же безлюдной технологии при таком подходе могут возникнуть существенные погрешности в расписании, которое является основой управления всей ГПС.
В указанных условиях большинство ГПМ имеют в своем составе различные накопители и магазины инструмента и оснастки (технологических ресурсов) для всех элементов (станка, манипулятора и т.п.). Состав технологических ресурсов довольно широк и складывается в процессе функционирования ГПМ в зависимости от последовательности поступления на обработку различных ПО, являющихся единицами планирования. При этом в случае поступления новой ПО состав ресурсов может, как соответствовать требуемому, так и значительно отличаться от него, и тогда приходится дооснащать ГПМ необходимыми ресурсами. Следовательно, время переналадки может колебаться от нуля до максимума.
Таким образом, время, затрачиваемое на переналадку ГПМ, зависит не только от состава технологических ресурсов, требуемого для обработки данной ПО, но и от состояния ГПМ на момент поступления этой ПО и от предыстории планирования, определяемой ранее обработанными ПО. Процесс переналадки ГПМ необходимо рассматривать как изменение его состояния S с точки зрения оснащения технологическими ресурсами. Чтобы выявить состояние ГПМ, а также состав и длительность операций переналадки, необходимо формализовать процедуру определения состава указанных операций.
По всей номенклатуре М обрабатываемых деталей требуемый состав Teij технологических ресурсов (здесь eij — ПО для i-x деталей и j-й операции) можно представить множеством h характеристик X требуемого состава ресурсов для выполнения данной ПО в виде следующего информационного массива:
Teij=[X1eij,X2eij,...,Xneij].
Эти характеристики представляют собой исходные данные технологического процесса (ТП) обработки ПО (требуемые оснастка, инструмент, параметры режимов обработки, выходные пара метры точности изготовления и т.п.). Для любой детали di (di Є M) и всей номенклатуры М создаются соответствующие информационные массивы:
Tdi=[[Tei1],[Tei2],...,[Teipi]];
TM=[[Td1],[Td2],...,[Tdm]];
здесь pi, — число операций при обработке детали di ; т — число наименований деталей в номенклатуре М.
Всю информацию о составе ГПМ также можно представить в виде массивов, характеризующих его следующие основные подсистемы: подсистему С технологического оборудования; подсистему R манипулирования заготовками и деталями; подсистему Z накопления заготовок и деталей.
Состояние любой подсистемы характеризуется составом как постоянных характеристик и функциональных возможностей, так и переменных технологических характеристик (оснастки и инструмента, устанавливаемых диапазонов функционирования узлов и механизмов и др.). Таким образом, для всех трех подсистем справедливо следующее отношение:
T0wk=Twk U T'wk; w Є {C,R,Z},
где T0wk — полное множество технологических характеристик w-й подсистемы k-го ГПМ; Twk и T'wk — множества соответственно постоянных и переменных характеристик той же подсистемы. Если постоянную и переменную части всей технологической информации, относящейся к k-му ГПМ, выразить соответственно как TГПМk=TCk U TRk U TZk и T'ГПМk=T'Ck U T'Rk U T'Zk , то какое-либо (l-е) состояние ГПМ при обработке ПО можно описать выражением
Slk(eij)=TГПМk U T'ГПМk.
Комплекс операций переналадок в ГПМ при поступлении (после обработки ПО еij) новой ПО eсо [т.е. при переходе ГПМ из l-го состояния в (l + 1)-е] в общем виде можно представить как Ql,l+1(eco)=f(Slk(el),Teco).
Для каждой из подсистем k-го ГПМ состав операций переналадок можно описать следующим
[Ql,l+1]wk=[Twecs]k\[Tw]k
где Тwecs — часть множества Тecs характеристик требуемого состава ресурсов для ПО еcs , относящаяся к w-й подсистеме ГПМ (таким образом, для обработки ПО еcs нужно подвергнуть переналадке те подсистемы ГПМ, переменная часть технологических характеристик которых не содержит требуемых ресурсов); T'w — множество переменных характеристик w-й подсистемы. Тогда полный состав процесса переналадок для k-го ГПМ:
[Ql,l+1]k=[Ql,l+1]Ck U [Ql,l+1]Rk U [Ql,l+1]Zk.
Задаваясь матрицей T’пер[t*пер] времен отдельных операций переналадки, можно определить общее время переналадок для k-гo ГПМ, а именно:

где r — число операций переналадки.
Поскольку весь комплекс отдельных операций переналадки может быть выполнен несколькими наладчиками, то в данном случае решается задача совмещения выполнения отдельных операций переналадки при критерии минимума календарной длительности выполнения всего комплекса работ и ограничениях на совместимость отдельных операций и последовательность их выполнения. Рассматривая такую задачу как задачу формирования расписания для детерминированной одностадийной системы с несколькими параллельными обслуживающими устройствами [5] и используя аддитивный алгоритм Э. Балаша [6], можно определить истинное значение tперeij времени переналадки ГПМ.
Задача, решение которой обеспечивает сокращение непроизводительных потерь времени в ГПС, с учетом изложенной методики, связанной с определением времени переналадок отдельных ГПМ, может быть сформулирована следующим образом: для номенклатуры деталей M{eij} и множества ГПМ в ГПС N{Nk) необходимо составить оптимальное расписание; в общем случае каждая ПО имеет постоянный размер aij партии запуска и может быть обработана на любом (k-м) ГПМ, что обусловливает многостадийность обслуживания.
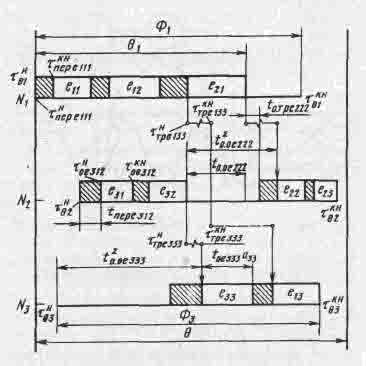
Рис. 1. Диаграмма расписания работы ГПС механической обработки.
Анализ немасштабированного произвольного расписания при указанных множествах, представленного диаграммой Гантта (рис. 1), показывает, что все непроизводительные времена при работе любого ГПМ (длительность tперeijk операций переналадок k-го ГПМ при поступлении на обработку ПО еij; время to.oeijk простоя k-го ГПМ из-за ожидания партии деталей, находящихся на обработке; время to.трeijk простоя k-го ГПМ из-за ожидания партии деталей, находящихся в процессе транспортирования) тесно взаимосвязаны и их соотношение существенно зависит от не детерминированности значения tперeij на момент составления расписания ГПС.
Обобщенная математическая модель задачи сокращения непроизводительного времени в ГПС (ее графическая интерпретация имеет вид сети G; рис. 2) представлена ниже:

Рис. 2. Графическая интерпретация задачи сокращения непроизводительного времени в ГПС, представленная в виде сети.
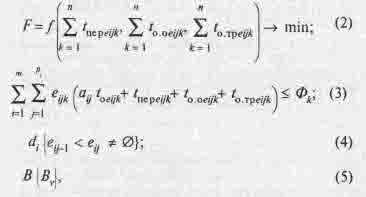
где m > 1; n >= 1; аij >0; аij = const; toeijk>0 — время, отводимое на выполнение j-й операции на k-м ГПМ; Фk — фонд времени работы k-го ГПМ; В — множество ограничений Bv, которые могут быть введены в модель с учетом конкретных условий.
Выражение (2) представляет собой функционал задачи в обобщенной форме, а выражение (3) — ограничение по фонду времени работы; выражение (4) отражает условие предшествования ПО согласно логике ТП; выражение (5) представляет собой обобщенный состав дополнительных ограничений (ограничения по директивным срокам выпуска деталей, приоритеты запусков и т.п.).
Вершинами сети G являются ПО еij, а ее дуги определяют возможность включения тех или иных ПО в расписание Ok того или иного ГПМ, а также в расписание O ГПС и несут на себе оценки времени переналадок. Горизонтальные ветви сети отождествляются с обрабатываемыми деталями, а источники N1,...,Nn — с теми ГПМ, для которых необходимо составить расписание; вершина t является стоком сети.
Особенностью данной сетевой модели является то, что на любом разрезе сети в начале планирования оценки весов всех дуг не определены. Их определение, согласно выражению (1), носит динамический характер и возможно лишь на этапе формирования расписания при фиксации всех состояний каждого ГПМ. Таким образом, задача построения расписания для ГПС представляет собой задачу построения такого пути (расписания O), состоящего из п отдельных расписаний, который включат бы в себя все вершины сети G, не содержал циклов и удовлетворял бы критерию (2) и условиям (3) — (5). Задачи подобного типа относятся к классу NP-полных задач сложного комбинаторного характера.
Для представленной модели оптимизации расписания были рассмотрены различные критерии и ограничения, которые могут быть использованы при планировании. Основными из критериев являются следующие:

Где F1 - критерий минимума времени переналадок в ГПМ; F2 — критерий минимума времени простоев ГПМ на транспортных операциях; F3 — критерий минимума времени простоев ГПМ в ожидании поступления ПО; F4 — интегральный критерий минимума всех непроизводительных времен. Кроме того, могут быть использованы критерии стоимостной структуры затрат, обусловленных непроизводительными потерями времени.
Для решения задачи формирования расписания разработан алгоритм на основе метода ветвей и границ (МВГ). При этом сеть G изображается в виде графа G', в котором каждая ПО представлена п раз, т.е. по числу ГПМ в ГПС. Тогда процесс формирования расписания O заключается в нахождении такого пути на графе G', который удовлетворял бы выбранному критерию и ограничениям задачи. Процесс поиска состоит во включении в путь (расписание O) ПО, удовлетворяющих следующим условиям аддитивности:
O {Ok(⊇ eijk)}=min F{(Slk,eijk),Sl1,...,Sln} ; (6)
Ф'k(ecsk)+to.oeijkaij+[max(τкнперeijk,τкнтрeijk)-τкнoecsk]≤Фk ; (7)
τноeijk-τкноei(j-1)≥0 . (8)
Выражение (6) означает выполнение условия по выбранному функционалу F задачи; выражение (7) представляет собой ограничение задачи по загрузке оборудования, а выражение (8) — условие предшествования ПО согласно логике ТП. Параметр Ф'к(есsk) — загрузка k-го ГПМ при включении в его расписание ПО ecsk, последней перед рассматриваемой ПО еijk, и его можно найти из следующего рекуррентного уравнения:
Ф'k(eijk)=Ф'k(ecsk)+toeijkaij+[max(τкнперeijk,τкнтрeijk)-τкнoecsk].
Формулы для определения параметров τ, входящих в выражения (7)—(9), несложно получить на основе анализа диаграммы Гантта (см. рис. 1).
Особенностью предлагаемого алгоритма является отсутствие у него нижней границы из-за неопределенности весов дуг сети на момент начала планирования, и поэтому роль указанной границы выполняет наилучшее для построенного пути текущее значение функционала F.
В целях реализации представленной концепции формирования оптимальных расписаний было разработано программное обеспечение для ГПС тс гарной группы. Численное моделирование с использованием данных различных предприятий показало следующее. При составлении расписания работы одного автономно работающего ГПМ наиболее эффективен критерий F1. Оптимальная последовательность загрузки деталей позволяет сократить общее время переналадок за смену на 10-15%.
При составлении расписания для ГПС, состоящей из нескольких ГПМ, наиболее эффективен критерий F4. Его применение обеспечивает сокращение в течение смены доли непроизводительного времени в среднем на 30—35% для каждого ГПМ (в том числе время переналадок сокращается на 7—10%). Все это позволяет увеличить загрузку ГПС в целом на 10—15% в смену.
Использование остальных критериев также увеличивает общую загрузку ГПС, но для повышения эффективности их применения необходимо вводить в модель (2)—(5) ограничения, зависящие от конкретных условий.
Таким образом, повышение производительности ГПС в результате оптимизации расписания возможно только при детальном анализе структуры непроизводительного времени. При определении длительности переналадок необходимо учитывать всю технологическую информацию, связанную с предысторией планирования. Длительность переналадок в ГПС не является детерминированной, и ее следует находить в процессе формирования расписания.
Предложенный подход к определению времени переналадок и составлению расписания ГПС позволяет значительно повысить точность расписания и его информативность, что является основой управления ГПС.