ДИЗЪЮНКТИВНОЕ ПЛАНИРОВАНИЕ

Цеховое планирование

      Проблема планирования определена множеством задач T и множеством ресурсов R. Задачи определяются отношениями старшинства, которые обязывают некоторые задачи ждать окончания других прежде, чем они могут начаться. Задачи, которые совместно используют ресурс, не прерываемые (неприоритетное планирование) и взаимоисключающие (дизъюнктивное в сравнении с кумулятивным планированием). Цель состоит в том, чтобы найти расписание, которое охватывает все задачи за минимальный промежуток времени.
      Формально, к каждой задаче t привязаны неотрицательные продолжительность d(t) и ресурсы use(t). Для отношений старшинства, precede(t1,t2 ) обозначает, что t₂ не может быть выполнена прежде, чем закончена t₁. Проблема состоит в том, чтобы найти множество начальных промежутков времени {time(t)}, которое минимизирует общее время работы по расписанию, определенное как Makespan:= max{time(t) + d(t)} при следующих ограничениях:



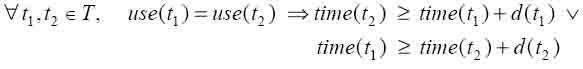
      Планирование цеха – это особый случай, в котором задачи сгруппированы в задания j¹,..., jⁿ. Задание jⁱ - последовательность задач j₁ⁱ,..., j_mⁱ, которые должны быть выполнены в этом порядке, то есть, для всех существует precede( j_kⁱ, j_k+1ⁱ). Такие проблемы называются n x m проблемами, где n – количество заданий и m - количество ресурсов. Сеть предшествования, таким образом, очень проста: она состоит из n "цепей". Упрощение берется не от матричной структуры (можно было всегда добавлять пустые задачи к проблеме планирования), а скорее от факта, что предшествование является функциональным отношением. Также предполагается, что каждая задача в задании выполняется на отдельном механизме (станке). Для задачи j_kⁱ целевая функция будет определена как сумма продолжительностей всех ее предшественников в этом задании, а остаток - как сумма продолжительностей всех последователей в этом задании, например: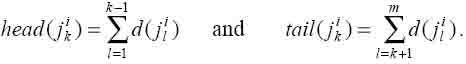


      Когда каждый позволяет отношениям старшинства формировать более сложную сеть, проблема определяется как дизъюнктивная проблема планирования. Хотя общие дизъюнктивные проблемы планирования часто являются более соответствующими для моделирования реальных ситуаций, небольшая работа по их уточнению была проведена (они были изучены более сообществом изучения проблем искусственного интеллекта, чем исследователями операций, и большинство опубликованных работ касается малых примеров, подобно известной проблеме мостовой конструкции с 42 задачами [VH89]). Интерес к n x m проблеме планирования возрос за прошлые 30 лет. Самый известный пример - 10 x 10 проблема Фишера и Томпсона [MT63], которая оставалась нерешенной до 1989 года, когда она была решена Карли и Пинсоном[CP89]. Классические эталонные тесты включают проблемы, случайно сгенерированные Адамсрм, Баласом и Заваком в 1988 [ABZ88], Эплгейтом и Куком в 1990 [AC91] и Лоренсом в 1984 [La84] годах. Из 40 проблем, опубликованных Лоренсом, одна все еще является нерешенной (20 x 10 упомянутая как LA29). Типичный размер этих эталонных тестов имеет размеры от 10 x 5 до 30 x 10.

Схема ветвей и границ с временными окнами

      Алгоритмы ветвей и границ, тем не менее, более изучены, и метод, эффективно используемый в [CP89] для решения MT10 является схемой ветвей и границ, названной "обнаружением границы". Так как расписание - это множество порядков выполнения задач на механизмах, естественным способом вычислить их шаг за шагом является определение порядка паре задач, которые совместно используют один и тот же ресурс, в каждом узле дерева поиска (который соответствует избавлению от дизъюнкции в формулировке ограничения). Существует множество возможностей, в зависимости от того, какую пару выбирать, как использовать дизъюнктивное ограничение прежде, чем пару фактически упорядочат, и т.д., но общая стратегия состоит в том, чтобы почти всегда определять порядок пар задач [AC91].
      Область определения, связанная с time(t_i), представлена как интервал: каждой задаче tⁱ соответствует окно (интервал) [t_i,¯t_i - d(t_i)], где t_i - минимальная стартовая дата, и t_i- максимальная дата завершения (таким образом, стартовая дата time(t_i) должна быть между t_i и t_i-d(t_i)). Во время поиска частичное упорядочение (<<) задач осуществлено следующим образом: t₁ << t₂<=>time(t₁)+d(t₁)<=time(t₂)
      Чтобы эффективно сокращать область поиска, необходимо иметь способность передавать решения, принятые в каждом узле дерева поиска. Таким образом, всякий раз, когда выбрано упорядочение, допустим t₁ << t₂, границы областей определения могут быть модифицированы следующим образом: t₂ >= t₁ + d(t₁) и t₁ <= t₂ - d(t₂) . При этой модели несогласованность может быть обнаружена, когда выполняется неравенство ¯t - t < d(t) для некоторой задачи t (t больше не попадает в свое окно (интервал)).