В настоящее время, когда возрастает важность наиболее эффективного использования природных и людских ресурсов, материальных и финансовых средств, особое значение приобретают задачи поиска оптимального решения той или иной проблемы.
Основные трудности численного решения экстремальной задачи связаны с ее размерностью и видом оптимизируемой (целевой) функции, которая в общем случае может быть нелинейной, недифференцируемой и многоэкстремальной. В каждом конкретном случае необходимо подбирать такой метод, который дает наиболее точное решение, а также следить затем, чтобы процедура поиска не была слишком продолжительной. Но случается, что традиционные методы и алгоритмы оптимизации из-за сложности задачи не дают желаемого результата, и поэтому возникает необходимость использования иных методов.
Одним из таких новых подходов, позволяющих преодолевать указанные трудности, является эволюционно-генетический подход. На его основе можно разрабатывать алгоритмы поиска оптимальных решений, которые получили название генетических алгоритмов.
Особенность подобных алгоритмов заключается в том, что в них используются механизмы, подобные механизмам популяционной генетики. Эти алгоритмы являются робастными (надёжными, устойчивыми) по отношению к виду оптимизируемой функции, а поиск оптимального решения в них осуществляется путем прямого манипулирования совокупностью из нескольких допустимых решений, образующих популяцию, каждое из которых представлено в некотором коде.
Целью данной работы является исследование и разработка программного обеспечения для решения некоторых оптимизационных задач на основе генетических алгоритмов и сравнительный анализ с традиционными методами.
Модели систем эволюции по аналогии с природными системами к настоящему времени можно разбить на две большие категории:
системы, которые смоделированы на биологических принципах. Они успешно использовались для задач типа функциональной оптимизации и могут легко быть описаны на небиологическом языке;
системы, которые являются биологически более реалистичными, но которые не оказались особенно полезными в прикладном смысле. Они больше похожи на биологические системы и менее направлены (или не направлены совсем), обладают сложным и интересным поведением и, видимо, вскоре получат практическое применение[1].
Надо отметить, что это деление условное, и во многих исследованиях эти направления комбинируются друг с другом. Рассмотренные категории представляют собой два полюса, между которыми лежат различные вычислительные системы. Ближе к первому полюсу расположены эволюционные алгоритмы, такие как эволюционное программирование (Evolutionary Programming), генетические алгоритмы (Genetic Algorithms) и эволюционные стратегии (Evolution Strategies). В настоящее время наблюдается взаимное проникновение указанных парадигм и их сращивание в единую концепцию эволюционных вычислений. Системы, которые могут быть классифицированы как «искусственная жизнь» (Artificial Life), находятся ближе ко второму полюсу [2].
Рассмотрим основные отличия генетических алгоритмов от традиционных.
1. Генетические алгоритмы работают с кодами, в которых представлен набор параметров, зависящих от аргументов целевой функции. Причем интерпретация этих кодов происходит только перед началом работы алгоритма и по его завершению. В процессе работы манипуляции с кодами происходят совершенно независимо от их интерпретации, код рассматривается просто как битовая строка.
2. Генетический алгоритм использует несколько точек поискового пространства одновременно, а не переходит от точки к точке, как это делается в некоторых традиционных методах. Это позволяет преодолеть один из их недостатков — опасность попадания в локальный экстремум целевой функции, если она не является унимодальной, т.е. имеет несколько экстремумов.
3. Генетические алгоритмы в процессе работы не используют дополнительной информации, что повышает скорость работы. Единственной используемой информацией может быть область допустимых значений параметров и целевой функции в произвольной точке.
4. Генетический алгоритм использует как вероятностные правила для порождения новых точек анализа, так и детерминированные правила для перехода от одних точек к другим. Одновременное использование элементов случайности и детерминированности дает значительно больший эффект, чем раздельное [3].
При разработке генетических алгоритмов важным является правильное представление хромосом как кодов (или битовых строк), в которых заключен набор параметров, напрямую зависящих от аргументов целевой функции.
Для проведения исследования алгоритмов и программ генетического поиска, а также для сравнения их с другими методами и алгоритмами рассмотрим типовую задачу оптимизации — задачу коммивояжера (Traveling Salesman Problem) [4]. Она формулируется следующим образом: коммивояжеру требуется объехать несколько городов, побывав в каждом из них один раз, и вернуться в исходную точку. Необходимо найти кратчайший маршрут.
В процессе разработки генетического алгоритма решения данной задачи были приняты некоторые обозначения. В качестве хромосом рассматриваются маршруты обхода — векторы, где в первой позиции стоит номер первого города на пути следования коммивояжера, затем номер второго и т.д. Операция мутации представляет собой перестановку значений двух случайно выбранных генов (номеров городов). По условию задачи в рассматриваемых хромосомах каждый ген должен встречаться только один раз.
Так как данная задача является комбинаторной, то для сравнения с генетическим алгоритмом были выбраны два традиционных метода решения подобных задач — метод перебора и метод ветвей и границ. Эти методы позволяют на основании косвенных оценок отбросить все те допустимые решения, среди которых не может быть оптимального. Однако недостатком данных методов является большая вычислительная сложность.
Другая известная категория методов решения оптимизационных задач — градиентные методы — идеальна для применения в так называемых унимодальных задачах, где целевая функция имеет единственный локальный экстремум, в то время как рассматриваемая в работе задача мультимодальна и многомерна. Для точного решения таких задач не существует универсальный метод. На практике комбинируют переборный и градиентный методы, чтобы получить хотя бы приближенное решение. Генетический алгоритм представляет собой именно комбинированный метод. Такая комбинация позволяет обеспечить устойчиво хорошую эффективность генетического поиска для любых задач.
Ниже приведена блок-схема генетического алгоритма, представленного в работе[5].
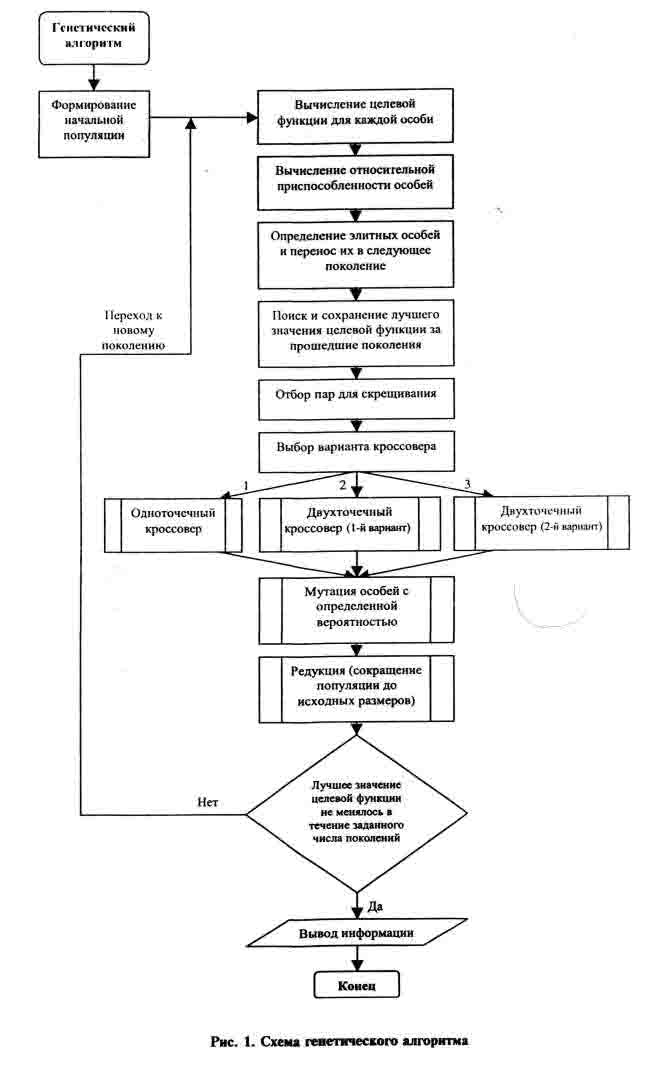
В начале действия генетического алгоритма формируется первое поколение особей. Далее происходит отбор нескольких элитных особей (если включена соответствующая стратегия) посредством вычисления и сравнения значений целевой функции для каждой особи. Элитными являются те особи, у которых полученные значения (в данной работе длина пути коммивояжера) являются наименьшими.
Программа позволяет использовать три вида скрещивания: одноточечный кроссовер и два варианта двухточечного кроссовера. Отбор скрещивающихся пар осуществляется при помощи генератора случайных чисел. На следующем этапе особи нового поколения с некоторой вероятностью подвергаются мутации. При процедуре редукции расширенная популяция сокращается до исходного размера за счёт удаления из неё особей с наихудшими значениями целевой функции. Окончание процесса эволюции происходит, если лучшее значение целевой функции не изменяется в течение заданного числа поколений. В работе на первой стадии были проведены исследования для отыскания таких значений параметров разработанного генетического алгоритма, которые обеспечивали бы наилучшую эффективность. Для генетического алгоритма были установлены следующие начальные характеристики:
- численность популяции;
- формирование в каждом поколении случайным образом некоторого числа «брачных пар» с заданной вероятностью;
- кроссовер: одноточечный, несколько разновидностей двухточечного;
- точечная мутация с устанавливаемой вероятностью;
- стратегия элитизма.
Поведение генетического алгоритма исследовалось при изменении ряда его параметров [6].
1. Элитизм. С точки зрения эффективности поиска этот эволюционный оператор в литературе характеризуется как достаточно слабый. В основном это объясняют потенциальной опасностью преждевременной сходимости [7]. Однако данные исследования показали, что использование именно элитного отбора является одним из наиболее эффективных действий по отношению к рассматриваемой задаче. Результаты тестирования, усредненные по 50 запускам, приведены в табл. 1, в первом столбце которой помещены величины отношения реального минимума FminGA к найденному генетическим алгоритмом минимальному значению целевой функции Fmin. Звездочкой отмечены эволюционные операторы (элитизм, одноточечный кроссовер и два варианта двухточечного кроссовера).
Таблица 1
Влияние генетических операторов на эффективность поиска
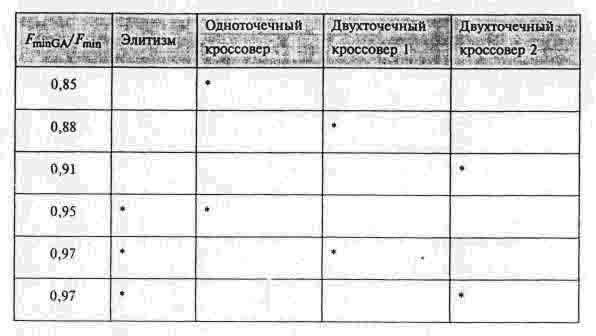
Время работы алгоритма, оцениваемое как сумма времени получения минимального значения целевой функции и времени, в течение которого ее значение не менялось на протяжении заданного числа поколений, при использовании различных операторов представлено в табл. 2. Изданных таблицы видно, что использование в последующих поколениях особей с наилучшим значением целевой функции приводит к резкому сокращению времени решения задачи.
Таблица 2
Влияние генетических операторов на время работы алгоритма

2. Сравнительный анализ
операторов кроссовера. Данные, приведенные на тех же диаграммах,
наглядно иллюстрируют лучшую эффективность генетического оператора Двухточечный
кроссовер 2 по отношению к операторам Одноточечный кроссовер 1 и Двухточечный
кроссовер 1.
3. Схема формирования родительских пар.
При формировании родительских пар используются две схемы: панмиксия (создание
пар из случайно выбранных особей) и генетический аутбридинг (когда пары могут
составить особи, генотипы которых максимально различны). Анализ результатов
исследований 40 запусков программы для данной задачи не позволил выявить
преимущество одной из схем [5].
4. Мутация и макромутация. При
решении ряда задач эффективность генетического алгоритма можно существенно
повысить, используя оператор мутации. Как уже отмечалось, оператор мутации
является «слабым» оператором. Но его роль возрастает в тех случаях, когда
требуется исследовать популяцию из локальных решений. Имеются в виду ситуации,
когда найден локальный экстремум целевой функции, тогда как оптимальному
решению соответствует только глобальный экстремум. Особенно эффективен в этом
отношении оператор макромутации. Экспериментальная проверка показала, что
использование оператора макромутации повышает точность генетического алгоритма;
это иллюстрирует рис. 2, где с помощью гистограмм оцениваются величины
отношения реального минимума к найденному минимальному значению целевой функции
для двух случаев.

После того, как были подобраны оптимальные
значения параметров генетического алгоритма и отлажена схема его работы, в
программу были включены традиционные методы решения выбранной типовой задачи —
метод перебора и метод ветвей и границ. Далее проводился сравнительный анализ
указанных методов и разработанного генетического алгоритма.
Были рассмотрены критерии для оценки
эффективности методов по наиболее важным параметрам:
- время работы алгоритма,
- точность получаемого решения, сходимость
алгоритма.
Важными пунктами для сравнения алгоритмов
являются следующие моменты:
устойчивость к входным данным;
требуемые ресурсы;
дружественный интерфейс пользователя.
Исследования показали, что хотя
генетический алгоритм не всегда находит оптимальное решение, но он
работоспособен в тех ситуациях, когда другие алгоритмы применить невозможно. На
рис. 3 приведены результаты тестирования, где в первом случае показано
количество найденных алгоритмами оптимальных решений, во втором — количество
эффективных решений и в третьем — число случаев, когда алгоритм не мог найти
сколько-нибудь приемлемого решения. Были решены 25 тестовых задач при одной и
той же схеме расположения городов для всех алгоритмов. Схема содержала 8
городов, положение которых каждый раз выбиралось случайно. Лучшие результаты
при данных условиях показал метод перебора, всегда находивший оптимальное
решение. Однако при числе городов свыше 10 метод перебора перестает работать
из-за возникновения конфликтной ситуации вследствие оперирования большим
количеством чисел высоких порядков.

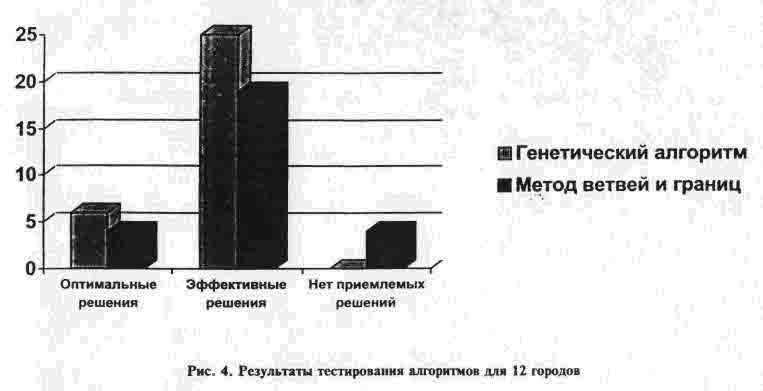
На рис. 4 представлены результаты
аналогичного тестирования алгоритмов для схем с 12 городами, расположенными
случайным образом. Запуск метода перебора в связи с увеличением количества
городов (больше 10) невозможен, поэтому соответствующие результаты на рисунке
не представлены. Суть исследованных и программно-реализованных в работе
генетических алгоритмов заключается в комбинированном подходе к проблеме.
Механизмы скрещивания и мутации в каком-то смысле реализуют переборную часть
метода, а отбор лучших решений — градиентный спуск. В работе показано, что
такая комбинация позво-ляет обеспечить устойчиво высокую эффективность
генетического поиска для любых типов задач.
Можно сделать вывод, что генетические
алгоритмы, будучи разновидностью методов поиска с элементами случайности,
позволяют находить эффективное решение задачи, а не оптимальное.
Для сложной системы часто требуется найти
удовлетворительное решение, а проблема достижения глобального оптимума отходит
на второй план. При этом другие методы, ориентированные на поиск именно
оптимального решения, вследствие чрезвычайной сложности задачи вообще
неприменимы. В этом кроется причина появления, развития и роста популярности
генетических алгоритмов.