Проанализирована точность расписания
оборудования в гибких производственных системах (ГПС) с учетом стохастичности
процессов, протекающих в них. Разработан алгоритм автоматического формирования
математических моделей вероятностного характера, позволяющий автоматизировать
процесс оценки надежности расписаний оборудования ГПС с использованием
вычислительной техники.
При формировании расписаний работы
оборудования в гибких производственных системах (ГПС) в большинстве случаев
доминирует номинальный характер, т.е. расписания строятся без учета влияния
фактора надежности элементов ГПС. В ряде случаев используются методы
резервирования времени в расписании работы оборудования по аналогии с работой
автоматических линий, ранжирования деталей по срочности и т.д. Использование
этих методов зачастую ухудшает область допустимого решения и сводит к нулю все
преимущества оптимизации при сокращении непроизводительных времен в расписании
работы ГПС.
В связи с этим предлагается метод учета
стохастичности процессов функционирования элементов ГПС при использовании ранее
построенных расписаний.
Рассмотрим функционирование ГПС, состоящей
из множества гибких производственных модулей (ГПМ) N={n}, транспортных средств
(ТС) R = {r} и складской системы (СС) S = {s = l}, как марковский случайный
процесс с простейшими потоками событий . Для упрощения расчетов обслуживающих
устройств в СС примем s=1, что имеет место в реальных ГПС.
С целью автоматизации анализа марковских
процессов в ГПС произвольной размерности N{n}xR{r}xS{s = l} предлагается
следующий алгоритм, позволяющий автоматически строить модель и оценивать
стохастические параметры процессов, протекающих в ГПС.
На первом шаге оценивается количество всех
состояний ГПС. Нулевым состоянием обозначим состояние, когда все элементы
исправны, т.е. G0 = {N1, N2 ..., Nn, R1, R2 ..., Rr, S1} - массив из (n + r +1)
элементов. Для упрощения модели считаем, что такой элемент ГПС как склад S1,
всегда находится в исправном состоянии. Остальные элементы (ГПМ и ТС) могут
выходить из строя как каждый в отдельности, так и вместе с каким-либо из других
элементов (или с несколькими из них). Сгенерированная путем перебора
последовательность состояний ГПС имеет вид:
G0 = {N1, N2 ..., Nn, R1, R2 ..., Rr, S1};
G1 = {N'1, N2 ..., Nn, R1, R2 ..., Rr, S1};
........................................................................
G2n+r-1 = {N'1,N'2 ...,N'n,R'1,R'2 ...,R'r, S1},
где элемент со штрихом означает, что данный элемент находится в неисправном
состоянии. Всего количество состояний у системы (вместе с состоянием G0 )
получается равным g = 2n+r и нумерация состояний идет от 1 до 2n+r-1.
На втором шаге составляем матрицу
переходов KП для множества состояний (1).
Переход из состояния Gi, в состояние Gj
осуществляется при следующих условиях:
Условие 1. Если неисправных
элементов в состоянии Gj больше, чем неисправных элементов в состоянии Gi,
только на один элемент.
Условие 2. Если в состоянии Gi,
какой-то элемент неисправен, то и в состоянии Gj этот элемент также должен быть
неисправен.
Если не выполняется хотя бы одно из этих
условий, то переход невозможен.
При этом считается, что из состояния Gi, в
состояние Gj переход осуществляется под действием потока интенсивностей отказов
элементов ГПС hij (*), а переход из Gj в Gi — под действием потока
окончаний ремонтов отказавших элементов ГПС µij. Потоки hij
и µij в дальнейшем идентифицируются с конкретными действиями,
например hN1, будет означать интенсивность отказов оборудования N1,
a µN1 — интенсивность окончания ремонтов данного обслуживающего
устройства. Матрица переходов из состояния Gi в состояние Gj представлена
табл.1.
Таблица 1
Структура матрицы переходов
| i |
j |
| 0 |
1 |
2 |
... |
2n+r-1 |
| 0 |
0 |
1 |
1 |
... |
0 |
| -1 |
0 |
|
... |
|
2n+r-1 |
| 2 |
-1 |
|
0 |
... |
|
| ... |
... |
... |
... |
0 |
... |
| 2n+r-1 |
0 |
|
|
... |
0 |
Матрица имеет 2n+r строк и 2n+r столбцов. Столбцы и
строки отвечают соответствующим состояниям G0,…,G2n+r-1 , в которые
осуществляется переход по графу состояний. Элементы матрицы KiiП =0.
Если переход из состояния Gi, в состояние Gj по приведенным выше условиям
невозможен, то соответствующие элементы KijП = 0. Если переход
возможен, то KijП = 1. Если в матрице элемент KijП = 1 ,
то автоматически элементу KijП присваивается значение (-1). Таким
образом, из состояния Gj можно перейти в состояние Gi, под действием потока
µij. Элементы матрицы заполняются в результате
последовательного просмотра последовательности состояний (1) и сравнения
отдельных состояний Gi , с остальными. Матрица переходов КП необходима
для составления известных линейных алгебраических уравнений вида (λi+λj)pk=µipi+µjpj,
полученных из соответствующих уравнений Колмогорова для последующего
определения финальных вероятностей состояний Gi.
Как известно, слева в каждом i-м уравнении
стоит вероятность данного состояния рi, умноженная на суммарную интенсивность
всех потоков, ведущих из данного состояния, а справа — сумма произведений
интенсивностей всех потоков, входящих в i-e состояние, на вероятности тех
состояний, из которых эти потоки исходят. В каждой строке и каждом столбце
матрицы имеем (n+r) ненулевых элементов. По строкам матрицы переходов КП
составляется левая часть уравнений, а по столбцам — правая часть.
Первым уравнением будет уравнение для
неизвестной финальной вероятности р0 . Чтобы его составить, нужно рассмотреть
нулевую строку и нулевой столбец переходной матрицы. Ненулевые элементы (-1 или
1) в строке матрицы показывают то, куда мы можем перейти из данного состояния,
а в столбце — те состояния, из которых можем перейти в данное. Значения КПij=1
показывают, что переход осуществляется под действием потоков отказов hij,
а значения KijП =-1 — что переход осуществляется под действием
потоков µij.
В результате аналогичных рассуждений
составляются все последующие уравнения для всех состояний ГПС, для чего
рассматриваются i-е строки j-е столбцы матрицы. В итоге получим систему 2n+r
уравнений, которую можно решить, если воспользоваться так называемым
нормировочным условием: р1+p2+…+p2n+r-1 = 1. При этом, как известно,
одно из уравнений отбрасывается, поскольку оно является следствием остальных.
Таким образом, предложенный алгоритм
позволяет автоматизировать формирование системы алгебраических уравнений
Колмогорова с целью определения всех финальных вероятностей ГПС. Значения
потоков событий hij и µij берутся как
среднестатистические по опыту эксплуатации ГПС. На рис.1 представлен граф
состояний для ГПС размерности N{2}xR{1}xS{1}.

Рис.1. Граф состояний
Последовательность состояний имеет вид
G0 = {N1, N2, R1, S1}; G1 = {N'1, N2,R1,
S1};
G2 = {N1,N'2, R1, S1}; G3 = {N1, N2 ,R'1,
S1};
G4 = {N'1,N'2, R1, S1}; G5 = {N'1, N2
,R'1, S1};
G6 = {N1,N'2,R'1, S1}; G7 = {N'1,N'1,R'1,
S1};
Матрица переходов представлена в табл. 2.
Таблица 2
Матрица переходов
| |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
| 1 |
-1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
| 2 |
-1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
| 3 |
-1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
| 4 |
0 |
-1 |
-1 |
0 |
0 |
0 |
0 |
1 |
| 5 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
1 |
| 6 |
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
1 |
| 7 |
0 |
0 |
0 |
0 |
-1 |
-1 |
-1 |
0 |
Система алгебраических уравнений модели
имеет вид:
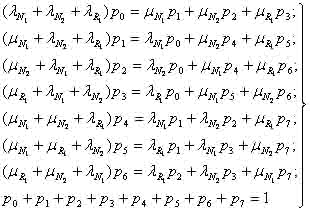 (2)
(2)
После определения финальных вероятностей
pi(i = 1,g) для всех состояний Gi, определяем долю времени, в течение которого
k-е обслуживающее устройство (ОУ), например ГПМ или ТС, проведет в нерабочем
состоянии:
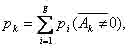 (3)
(3)
где выражение под знаком суммы — сумма
финальных вероятностей для какого-либо неработающего k-го ОУ Ak(N'k
либо R'k).
Далее определим, сколько времени k-е ОУ
будет находиться в неработающем состоянии в течение запланированного срока:
tрмk=Фkрk (4)
где Фk — фонд времени работы
k-го ОУ.
В большинстве случаев величину фонда времени Фk можно
принимать равной величине горизонта планирования O. В первую очередь
рассматривается ОУ, которое имеет наибольшую финальную вероятность рk
и время tрмк; затем анализируется вероятность выхода данного ОУ из
строя. Поскольку неизвестно, в какой момент времени данное ОУ выйдет из строя,
то необходимо рассмотреть все интервалы времени. Наиболее неблагоприятными
интервалами времени, в которых отказ ОУ приводит к наихудшим последствиям,
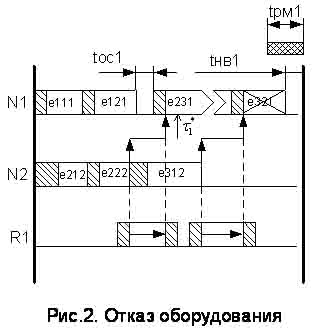
являются интервалы, в которых ведется обработка партий деталей. На рис. 2
представлено произвольное, не масштабированное расписание работы ГПС из трех
ОУ, из которых два являются технологическими ОУ (ГПМ). В процессе обработки
единицы планирования e231 в момент времени т*1
происходит отказ ОУ N1, которое будет находиться в состоянии ремонта, согласно
(4), в течение времени tрм1=Ф1р1. В случае отказа какого-либо ОУ
возможно два варианта действий — сдвиг расписания вправо по оси времени и
пересчет расписания. Рассмотрим ситуацию со сдвигом расписания, хотя ход
дальнейших действий с таким же успехом можно было бы проецировать и на вариант
с пересчетом расписания.
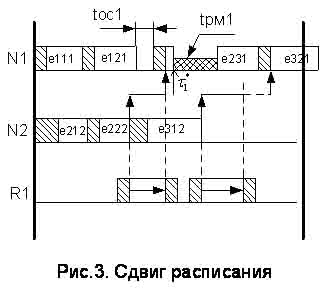
При сдвиге расписания (рис. 3) необходимо,
чтобы в расписании отказавшего ОУ для любого k-го ГПМ выполнялось простое
неравенство:
tрмk< tOCktHBk
(5)
где tOCk – время простоя ОУ по
причине нерационально составленного расписания; tHBk –
неиспользованное время в конце горизонта планирования.
Если это условие не выполняется, то
расписание работы ОУ после ремонта обязательно выйдет за пределы горизонта
планирования. Однако выполнение данного условия далеко не всегда дает
положительный результат, даже если заявка еijk имеет резервы времени
в виде величины tOCk. В частности, сдвиг расписания приводит к
нарушению сроков выполнения работ в системе — работы не укладываются в горизонт
планирования.
Если величина рk является такой,
что отказ на любой заявке может привести к сдвигу расписания за пределы
горизонта планирования, то целесообразно вводить дублирующее ОУ . В данном
случае ввод в действие дублирующего ОУ гарантирует, что при рассмотренной схеме
отказа расписание будет выполнено в пределах заданного горизонта планирования.
Необходимо отметить, что подобный анализ необходимо проводить для каждой
единицы планирования eijk на рассматриваемом k-м ОУ. Не во всех
случаях отказ ОУ приведет к нарушению сроков плана, но в результате такого
исчерпывающего анализа будем иметь полную картину всех вариантов возможных
нарушений расписаний.
Предложенный метод автоматизации анализа
надежности расписаний в ГПС позволил создать соответствующее программное
обеспечение, что значительно сократило время на создание моделей и оценку
надежности ранее построенных расписаний.
* По тексту hij - λij в формулах.

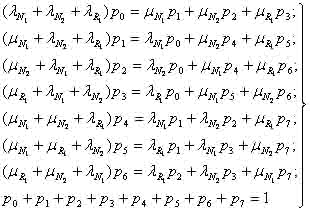 (2)
(2)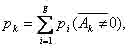 (3)
(3)
