После выбора кодирования, второе решение
при использовании генетического алгоритма – это как исполнить выбор, то есть,
как выбрать индивидуумы в популяции, которые создадут потомство для следующего
поколения, и сколько потомства каждый создаст. Цель выбора состоит в том,
чтобы, конечно, подчеркнуть значимости индивидуумов в популяции в надежде, что
их потомство будет, в свою очередь, иметь более высокую значимость. Выбор
должен быть сбалансирован изменениями в последствии кроссинговера и мутации
("равновесие эксплуатации/исследования"): сверх крепкий выбор означает, что
локально оптимальные значимые индивидуумы примут популяцию, сокращая
разнообразие, необходимое для дальнейшего изменения и продвижения; сверх слабый
выбор приведет к сверх медленному развитию. Относительно кодирования
многочисленные схемы выбора были предложены в литературе по ГА. Ниже я опишу
некоторые из самых распространенных методов. Относительно кодирования эти
описания не обеспечивают строгие рекомендации, при которых метод должен
использоваться относительно определенной проблемы; это все еще открытый вопрос
для ГА. (Для большего количества технических сравнений различных методов
выбора, см. Goldberg и Deb 1991, Back и Hoffmeister 1991, de la Maza и Tidor
1993, и Hancock 1994.)
Пропорционально Значимый Выбор с "Колесом Рулетки" и
"Стохастическое Универсальное" Осуществление Выборки
Оригинальный ГА Holland’а
использовал пропорционально значимый выбор, в котором "ожидаемое значение"
индивидуума (то есть, ожидаемое число раз, которое индивидуум будет выбран для
воспроизведения) равна значимости индивидуума, разделенной на среднюю
значимость популяции. Самый распространенный метод для того, чтобы осуществлять
это - "осуществление выборки" колеса рулетки, описанный в главе 1: каждому
индивидууму соответствует сектор кругового "колеса рулетки", размер сектора
которого является пропорциональным значимости индивидуума. Колесо крутят N раз,
где N - номер индивидуумов в популяции. На каждом вращении, индивидуум под
маркером колеса выбран, чтобы находиться в группе родителей для следующего
поколения. Этот метод может быть осуществлен следующим образом:
-
Суммировать общее количество ожидаемых значений индивидуумов в популяции.
Назовем эту сумму T.
-
Повторите N раз:
Выберите случайное целое
число r между 0 и T.
Цикл по индивидуумам в популяции, подводя
итог ожидаемых значений, пока сумма не станет больше или равной r. Индивидуум,
ожидаемое значение которого выводит сумму из этого предела, является избранным.
Этот стохастический метод статистически
приводит к ожидаемому числу потомства для каждого индивидуума. Однако, с
относительно маленькими популяциями, типично используемыми в ГА, фактическое
количество потомства, распределенного индивидууму часто далеко от его
ожидаемого значения (чрезвычайно маловероятный ряд вращений колеса рулетки мог
даже распределить все потомство самому плохому индивидууму в популяции). James
Baker (1987) предложил другой выборочный метод - "стохастическое универсальное
осуществление выборки" (SUS) - чтобы свернуть это "распространение" (диапазон
возможных фактических значений, учитывая ожидаемое значение). Вместо того чтобы
вращать колесо рулетки N раз для того, чтобы выбрать N родителей, SUS вращает
колесо один раз, но с N одинаково расположенными указателями, которые
используются при выборе N родителей. Baker (1987) дает следующий фрагмент кода
для SUS (в C):
ptr = Rand(); /* Returns random number uniformly distributed in [0,1]*/
for (sum = i = 0; i < N; i + + )
for (sum += ExpVal(i,t); sum > ptr; ptr++)
Select
(i);
где i - индекс по членам совокупности и где ExpVal (i, t) дает ожидаемое
значение индивидуума i во время t. Под этим методом, каждый
индивидуум i, как гарантируют, воспроизведется не менее ExpVal (i, t)
раз, но не больше, чем ExpVal (i, t) раз. (Доказательство этого оставляют как
упражнение.)
SUS не решает главные проблемы с
пропорционально значимым выбором. Как правило, ранее в поиске дисперсия
значимости в популяции высока, и небольшое количество индивидуумов более
значимо, чем другие. При пропорционально значимом выборе, они и их потомки
множатся быстро в популяции, в действительности, препятствуя ГА сделать любое
дальнейшее исследование. Это известно как "преждевременная конвергенция".
Другими словами, пропорционально значимый выбор вначале часто делает слишком
большой акцент на "эксплуатацию" весьма пригодных строк за счет исследования
других регионов области поиска. Позже в поиске, когда все индивидуумы в
популяции очень похожи (дисперсия значимости низкая), нет никаких реальных
различий значимости для выбора эксплуатации, и развитие следует к ближайшему
выходу. Таким образом, разряд развития зависит от дисперсии значимости в
популяции.
Сигма-Масштабирование
Обращаясь к таким проблемам,
исследователи ГА экспериментировали с несколькими видами методов
"масштабирования" для того, чтобы отобразить "необработанные" значения
значимости к ожидаемым значениям, чтобы сделать ГА менее восприимчивым к
преждевременной конвергенции. Один пример - "сигма-масштабирование " (Forrest
1985; это называли "усечением сигмы" в Goldberg 1989), которое сохраняет
давление выбора (то есть, степень, при которой очень пригодным индивидуумам
разрешают большое количество потомства), относительно постоянный в течение
выполнения, а не зависящий от дисперсий значимости в популяции. При
сигма-масштабировании ожидаемое значение индивидуума – это функция значимости
его популяции, среднего и среднеквадратичного отклонения популяции. Пример
сигма-масштабирования будет
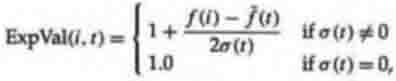
где ExpVal (i, t) - ожидаемое значение индивидуума i во время t, f(i) -
значимость i, f (t) – средняя значимость популяции во время t, и А(t)-
среднеквадратичное отклонение значимости популяции во время t. Эта функция,
используемая в работе Tanese (1989), дает индивидууму со значимостью одно
среднеквадратичное отклонение выше среднего 1.5 ожидаемого потомства. Если
ExpVal (i, t) был, меньше чем 0, Tanese произвольно сбрасывают это к 0.1 для
того, чтобы индивидуумы с очень низкой значимостью имели некоторый маленький
шанс на репродуцирование.
В начале выполнения, когда
среднеквадратичное отклонение значимости типично высоко, индивидуумы не будут
значимее средних по среднеквадратичными отклонениям, поэтому они не будут
распределены в большей степени в потомстве. Аналогично, позже в выполнении,
когда совокупность типично более сходится и среднеквадратичное отклонение
типично ниже, индивидуумы значимее, что позволяет развитию продолжиться.
Элитизм
"Элитизм", впервые
представленный Кеннетом Ди Джонгом (1975), является добавлением ко многим
методам выбора, которое вынуждает ГА сохранять некоторое количество лучших
индивидуумов в каждом поколении. Такие индивидуумы могут быть потеряны, если
они не выбраны, чтобы воспроизвести или если они разрушены пересечением или
мутацией. Много исследователей нашли, что элитизм значительно улучшает
выполнение ГА.
Выбор Boltzmann’а
Сигма-масштабирование
сохраняет значение выбора большей степенью на выполнении. Но часто различные
количества значимости выбора необходимы в разное время – например, ранее для
этого мог бы быть хорош либеральный подход, разрешая менее пригодным
индивидуумам воспроизводиться вместе с более пригодными индивидуумами, и имея
выбор медленного проведения при поддержании большого количества в популяции.
Позже могло бы быть хорошо иметь выбор между более значимыми, чтобы придать
особое значение очень пригодным индивидуумам, предполагая, что раннее
разнообразие с медленным выбором позволило совокупности находить верную часть
области поиска.
Один из подходов к этому - "Выбор
Boltzmann’а" (подход, подобный моделируемому отжигу), в котором непрерывно
изменяющаяся "температура" управляет разрядом выбора согласно предварительно
установленному графику. Температура начинается с высокого значения, что
означает, что значение выбора низко (то есть, каждый индивидуум имеет немного
разумной вероятности репродуцирования). Температура постепенно понижается, тем
самым постепенно увеличивается значение выбора, таким образом позволяя ГА
сузиться в более близкую к лучшей части области поиска при поддержании
"соответствующей" степени разнообразия. Для примеров этого подхода, см.
Goldberg 1990, de la Maza и Tidor 1991 и 1993, и Priigel-Benneth и Shapiro
1994. Типичное выполнение должно назначить на каждого индивидуума i ожидаемое
значение,
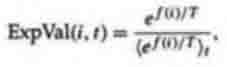
где T - температура, и <> t обозначает среднее количество по популяции во время
t. Экспериментирование с этой формулой покажет, как при уменьшении T,
изменяется ExpVal (i, t) между высокими и низкими увеличениями значимости. Цель
состоит в том, чтобы это происходило постепенно в течение поиска, чтобы
температура постепенно уменьшалась согласно предопределенному графику. De la
Maza и Tidor (1991) определили, что этот метод превзошел по быстродействию
пропорционально значимый выбор на малом наборе тестовых задач. Они также (1993)
сравнили немного теоретических свойств этих двух методов.
Пропорционально значимый выбор обычно
используется в ГА, главным образом, потому что это была часть оригинального
предложения Holland’а и потому что это используется в Теореме Схемы, но,
очевидно, для многих приложений, простой пропорционально значимый выбор
требует, чтобы несколько "местоположений" способствовали приемлемому
выполнению. В последние годы полностью отличные подходы к выбору (например,
рангу и выбору турнира) стали все более и более распространены.
Выбор Ранга
Выбор ранга - альтернативный
метод, цель которого состоит в том, чтобы также предотвратить сверхбыструю
конвергенцию. В версии, предложенной Backer’ом (1985), особи в популяции
ранжированы согласно значимости, и ожидаемое значение каждой особи зависит от
ее ранга, а не от ее абсолютной значимости. Нет никакой потребности
масштабировать значимость в этом случае, так как абсолютные различия в
значимости затенены. Этот отказ абсолютной информации значимости может иметь
преимущества (использующий абсолютную значимость, может вести к проблемам
конвергенции), и недостатки (в некоторых случаях могло бы важно знать, что одна
особь более значима, чем ее самый близкий конкурент). Ранжирование избегает
составления далекой наибольшей доли потомства маленькой группы очень пригодных
особей, и таким образом, уменьшает давление выбора, когда дисперсия значимости
высока. Это также поддерживает на высоком уровне давление выбора, когда
дисперсия значимости низка: коэффициент ожидаемых значений особей i и i+1 будет
тот же самый, не смотря на то, высоки ли их абсолютные различия значимости или
низки.
Линейный метод ранжирования, предложенный
Backer’ом, следующий: Каждая особь в популяции ранжирована в увеличивающемся
порядке значимости, от 1 до N. Пользователь выбирает ожидаемое значение Max
особи с рангом N, с Max e0. Ожидаемым значением каждой особи i в
популяции во время t составляет
 (5.1)
(5.1)
где Min - ожидаемое значение особи с рангом 1. Учитывая ограничения Max e0
и iExpVal (i, t) = N (так как совокупность устанавливает размеры константы
пребывания от поколения до поколения), требуется, чтобы 1 d Maxd 2 и Min = 2 Max
(совокупность этих требований оставляют как упражнение).
В каждом поколении особи в популяции
ранжированы и им назначены ожидаемые значения согласно уравнению 5.1.
Backer рекомендовал Max =1.1 и показал, что эта схема адекватна по сравнению с
пропорционально значимым выбором на некоторых выбранных тестовых задачах. Выбор
ранга имеет возможный недостаток: замедление давления выбора означает, что ГА в
некоторых случаях будет медленнее в обнаружении очень пригодных личностей.
Однако, во многих случаях увеличенное сохранение разнообразия, которое следует
из занимающих место выводов к более успешному поиску, чем быстрая конвергенция,
которая может следовать из пропорционально значимого выбора. Разнообразие
других схем ранжирования (типа показательного, а не линейного ранжирования)
также опробовано. Для любого метода ранжирования, ожидаемые значения которых
были обозначены, SUS метод может использоваться, чтобы произвести выборку
популяции (то есть, выбрать родителей).
Как было описано в главе 2,
разновидность выбора ранга с элитизмом использовали Mayer и Packard для того,
чтобы развить наборы состояния, также мои коллеги и я использовали подобную
схему развития ячеистых автоматов. В тех примерах популяция была ранжирована
значимостью, и вершина E строки была выбрана, чтобы быть родителями. N-E
потомков были объединены с E родителями, чтобы создать следующую совокупность.
Как было упомянуто выше, это форма так называемых (1/4 + ») стратегий,
используемая в семействе стратегий развития. Этот метод может быть полезен в
случаях, где функция значимости является шумной (то есть, - случайная
переменная, возможно, возвращает различные значения на различных запросах на
той же самой особи); лучшие особи сохранены так, чтобы они могли быть проверены
снова и, таким образом, через какое-то время, получить все более и более
надежные оценки значимости.
Выбор Турнира
Пропорционально значимые
методы, описанные выше, требуют двух проходов через популяцию в каждом
поколении: один проход, чтобы вычислить среднюю значимость (для
сигма-масштабирования среднеквадратичное отклонение) и один проход, чтобы
вычислить ожидаемое значение каждой особи. Масштабирование ранга требует
сортировки полной популяции рангами, а это потенциально отнимающая много
времени процедура. Выбор турнира также ранжирует выбор в терминах давления
выбора, но это в вычислительном отношении более эффективно и более податливо к
параллельному выполнению.
Две личности выбраны наугад из
совокупности. Случайное число r выбрано между 0 и 1. Если r< k (где k -
параметр, например 0.75), более значимая из этих двух особей выбрана, чтобы
быть родителем; иначе менее пригодная выбрана. Эти две возвращены к
первоначальной популяции и могут быть выбраны снова. Анализ этого метода был
представлен Goldberg и Deb (1991).
Установившийся Выбор
Большинство ГА, описанных в
литературе было "потомственным" – в каждом поколении новая популяция состоит
полностью из потомства, сформированного родителями в предыдущем поколении (хотя
некоторые из их потомств могут быть идентичны их родителям). В некоторых
схемах, типа элитарных схем, описанных выше, последовательное перекрытие
поколений в некоторой степени от некоего предыдущего поколения сохранено в
новой совокупности. Долю новых личностей в каждом поколении назвали
"промежуточным поколением" (De Jong 1975). В установившемся выборе только
несколько личностей заменены в каждом поколении: обычно небольшое количество
наименее пригодных особей заменено потомством, следующим из пересечения и
мутации самых пригодных личностей. Установившиеся ГА часто используются в
развитии систем на основе правил (например, системы классификатора; см. Holland
1986), в каком возрастающем изучении (и запоминание, что был уже изучен), в
котором члены популяции рассматриваются все вместе (а не индивидуально), решают
проблему быстро. Установившийся выбор был проанализирован Syswerda (1989,
1991), Whitley (1989), и De Jong и Sarma (1993).
ГЕНЕТИЧЕСКИЕ ОПЕРАТОРЫ
Третье решение осуществления
генетического алгоритма состоит в том, какие генетические операторы
использовать. Это решение очень зависит от стратегии кодирования. Здесь я буду
обсуждать пересечение и мутацию, главным образом, в контексте кодирования
строки битов, и я упомяну множество других операторов, которые были предложены
в ГА литературе.
Кроссинговер
Можно сказать, что главной
отличительной особенностью ГА является использование кроссинговера.
Одноточечный кроссинговер - самая простая форма: единственная позиция
пересечения и части двух родителей выбраны наугад после того, как позиция
пересечения обменена, чтобы формировать два потомства. Идея здесь должна,
конечно, повторно объединить стандартные блоки (схемы) на различных строках.
Одноточечный кроссинговер имеет, однако, некоторые недостатки. С одной стороны,
это не может объединить все возможные схемы. Например, это не может в общих
образцах объединения 11***** 1 и ****ll**, чтобы формировать образец 11**11*1.
Аналогично, схемы с большими длинами определения, вероятно, будут разрушены под
одноточечным кроссинговером. Eshelman, Caruana, и Schaffer (1989) назвали это
"позиционным смещением": схемы, которые могут быть созданы или разрушены
пересечением, зависят строго от местоположения битов в хромосоме. Одноточечный
кроссинговер предполагает, что короткие, младшие схемы – функциональные
стандартные блоки строк, но каждый вообще не знает заранее, какое упорядочение
битов группирует функционально связанные биты вместе – это было целью оператора
инверсии и других адаптивных операторов, описанных выше. Eshelman, Caruana, и
Schaffer также указывают, что не может быть никакого пути поместить все
функционально связанные биты близко друг к другу в строку, так как
специфические биты могли бы быть критическими больше чем в одной схеме. Они
указывают далее, что тенденция одноточечного кроссинговера для сохранения
коротких схем неповрежденными может вести к сохранению попутных битов, которые
не являются частью желательной схемы, но которые, будучи близкими на строке,
сопутствуют наряду с выгодной схемой при воспроизводстве. (Это было замечено в
"Королевских Дорожных" экспериментах, описано вышеупомянутое в главе 4.) Много
людей также отметили, что одноточечный кроссинговер обрабатывает некоторые
местоположения предпочтительно: доли, обмененные между этими двумя родителями,
всегда содержат оконечные точки строк.
Чтобы уменьшать позиционное смещение и этот
эффект "оконечной точки", много практиков ГА используют пересечение с двумя
точками, в котором две позиции выбраны наугад, и доли между ними обменены.
Пересечение с двумя точками, менее вероятно разрушит схемы с большими длинами
определения и может объединить больше схем, чем одноточечный кроссинговер.
Кроме того, доли, которые обменены, не обязательно содержат оконечные точки
строк. Снова, есть схемы, которые пересечение с двумя точками не может
объединить. Практики ГА экспериментировали с различными количествами точек
пересечения (в одном методе, количество точек пересечения для каждой пары
родителей выбрано из распределения Пуассона по среднему значению – функция
длины хромосомы). Некоторые практики (например, Spears и De Jong (1991)) верят
строго в превосходство "параметризированного однородного пересечения", в
котором обмен случается в каждой разрядной позиции с вероятностью p (типично
0.5 разности потенциалов d 0.8). Параметризированное однородное пересечение не
имеет никакого позиционного смещения - любые схемы, содержавшиеся в различных
позициях в родителях, могут потенциально быть повторно объединены в потомстве.
Однако этот недостаток позиционного смещения может предотвратить
перераспределенные аллели от когда-либо сформированных в популяции, так как
параметризированное однородное пересечение может быть очень подрывным в любой
схеме.
Учитывая эти (и много других вариантов
пересечения, найденных в литературе по ГА), какие Вы должны использовать? Нет
никакого простого ответа; успех или неудача специфического оператора
пересечения зависят сложными способами на специфической функции значимости,
кодировании, и других подробностях ГА. Это все еще очень важная открытая
проблема, которая состоит в полном понимании этих взаимодействий. Есть много
газет в литературе по ГА, определяющих количество аспектов различных операторов
пересечения (позиционное смещение, потенциал сбоя, способность создать
различные схемы в одном шаге и так далее), но они не дают категорическое
руководство о том, когда использовать некоторый тип пересечения. Есть также
много газет, в которых полноценность различных типов пересечения опытным путем
сравнена, но все эти изучения полагаются на специфические маленькие наборы
программ испытательных функций, и различные изучения дают противоречивые
результаты. Снова необходимо подобрать общие заключения. Это рассматривается в
недавних приложениях ГА, чтобы использовать или пересечение с двумя точками или
параметризированное однородное пересечение с p H 0.7-0.8.
Главным образом, комментарии и
вышеупомянутые справочники имеют дело с пересечением в контексте кодирования
строки битов, хотя некоторые из них обращаются к другим типам кодирования
также. Некоторые типы кодирования требуют специально определенного пересечения
и операторов, например, мутации, кодирования дерева, используемого в
генетическом программировании, или кодировании для проблем подобно Проблеме
Коммивояжера (в котором задача состоит в том, чтобы найти правильное
упорядочение для коллекции объектов).
Большинство комментариев также
предполагает, что способность пересечения повторно объединять очень пригодные
схемы является разумной, это должно быть полезно. Учитывая некоторые из
вызовов, мы позаботились об уместности схем как инструмента анализа для того,
чтобы понять ГА, можно было спросить, если мы не рассмотрели возможность, что
пересечение является фактически полезным по некоторой полностью различной
причине (например, именно, в сущности, оператор "макромутации" просто учитывает
большие переходы в области поиска). Я должен оставить этот вопрос открытым в
области исследования ГА для заинтересованных в исследованиях читателей. (Terry
Jones (1995) выполнил несколько интересных, хотя и предварительных,
экспериментов, пытающихся выделить возможные различные роли пересечения в ГА).
Его ответ мог бы также пролить свет по вопросу о том, почему рекомбинация
полезна для реальных организмов (если действительно это так) –пока это спорно,
и все еще нужно открывать вопрос в эволюционной биологии.
Мутация
Общее представление в
сообществе ГА относится к книге Holland’а Адаптации в Естественных и
Искусственных Системах и является тем пересечением. Главным прибором изменения
и новшества в ГА является мутация, обеспечивающая популяцию средствами против
постоянной фиксации в любом специфическом местоположении и, таким образом,
играющая больше фоновую роль. Это отличается от традиционных позиций других
эволюционных методов вычисления, типа эволюционного программирования и ранних
версий стратегий развития, в которых случайная мутация является единственным
источником изменения. (Более поздние версии стратегий развития включили форму
пересечения).
Однако оценка роли мутации растет,
поскольку сообщество ГА пытается понять, как ГА решают сложные проблемы.
Некоторые сравнительные занятия были выполнены мною на значимости мутации
против пересечения; например, Spears (1993) формально проверил интуитивную идею
того, что в то время, как мутация и пересечение имеют ту же самую способность к
"сбою" существующих схем, пересечение является более устойчивым "конструктором"
новых схем. Muhlenbein (1992, p. 15), с другой стороны, утверждает, что во
многих случаях более удачливая стратегия будет работать лучше, чем ГА с
пересечением и что «влияние мутации было недооценено в традиционных
генетических алгоритмах». Как мы видели в Королевских Дорожных экспериментах в главе
4. это не выбор между пересечением или мутацией, а скорее равновесие
среди пересечения, мутации, и выбора, который из них является более важным.
Правильное равновесие также зависит от подробностей функции значимости и
кодирования. Кроме того, пересечение и мутация изменяются по относительной
полноценности в течение выполнения. Более точное описание того, как все это
случается, все еще требует объяснения. По моему мнению, наиболее перспективное
направление, чтобы производить правила балансировки в течение выполнения,
состоит в нахождении пути для ГА, чтобы приспособить его собственную мутацию и
нормы пересечения в течение поиска. Некоторые попытки этого будут описаны ниже.
Другие Операторы и Совмещающиеся Стратегии
Хотя большинство приложений
ГА использует только пересечение и мутацию, существует много других операторов
и стратегий применения, которые исследовались в литературе по ГА. Они включают
инверсию и удвоение гена (обсужденный выше) и несколько операторов для того,
чтобы сохранить разнообразие в популяции. Например, De Jong (1975)
экспериментировал с оператором "уплотнения", в котором недавно сформированное
потомство заменяло существующую особь, наиболее подобную себе. Это
предотвратило слишком много подобных особей ("уплотнения") от того, чтобы быть
в популяции в одно и то же время. Goldberg и Richardson (1987) достигали
подобного результата, используя явную "совместно используемую значимую"
функцию: значимость каждой особи была уменьшена на присутствие других членов
популяции, где количеством уменьшения друг из-за друга член популяции была
явная увеличивающаяся функция подобия между этими двумя особями. Таким образом,
особи, которые были подобны многим другим особям, были наказаны, а особи,
которые были различны, были вознаграждены. Goldberg и Richardson показали, что
в некоторых случаях это могло вызвать соответствующее "видообразование",
разрешая членам совокупности сходиться на нескольких пиках в ландшафте
значимости, а не всем на схождении к тому же самому пику. Smith, Forrest и
Perelson (1993) показали, что подобный эффект мог быть получен без присутствия
явной функции совместного использования.
Различный способ продвигать разнообразие
состоит в том, чтобы поместить ограничения на совмещение. Например, если только
достаточно подобным особям разрешают совместиться, отличные "разновидности"
(совмещающиеся группы) будут иметь тенденцию формироваться. Этот подход был
изучен Deb и Goldberg (1989). Eshelman (1991) и Eshelman и Schaffer (1991)
использовали противоположный путь: они отвергли совмещения между достаточно
подобными особями ("кровосмешение"). Их желание не состояло в том, чтобы
формировать разновидности, а скорее сохранять полную совокупность настолько
разнообразной, насколько это возможно. Holland (1975) и Booker (1985)
предложилb использовать "совмещающиеся тэгы" - части хромосомы, которые
идентифицируют предполагаемых помощников друг другу. Только тем особям с
соответствием тэгов разрешают совместиться (своего рода процедура "сексуального
выбора"). Эти тэги, в принципе, развились бы наряду с остальной частью
хромосомы, чтобы адаптивно осуществить соответствующие ограничения на
совмещение. Наконец, были некоторые эксперименты с пространственно ограниченным
совмещением (см., например, Hillis 1992): совокупность развивается на
пространственной решетке, и особи, вероятно, совместятся только с особями в их
пространственном соседстве. Hillis нашел, что такая схема помогла сохранять
разнообразие, поддерживая пространственно изолированные разновидности, с
новшествами, в значительной степени встречающимися в границах между
разновидностями.
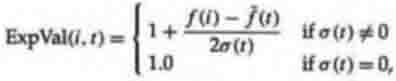
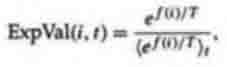
 (5.1)
(5.1)