В настоящее время, в условиях начавшегося роста производства и необходимости совершенствования методов планирования и управления производством, исследования в области математического моделирования производственных процессов вновь становятся актуальными.
      В данном сообщении предлагается одна математическая модель, которая может найти применение в практике планирования и управления серийным машиностроительным производством.
      В машиностроительном производстве технологические процессы изготовления изделий, входящих в них деталей, сборочных единиц, расчленяются на отдельные операции, между которыми возможны прерывания процессов изготовления, вызванные необходимостью транспортировки деталей с одного участка на другой либо ожиданием очередной обработки на оборудовании, которое в данный момент занято другой работой. Промежуток времени между запуском деталей в обработку и выпуском готовых изделий, при сборке которых эти детали используются, называется технологическим опережением.
      В производстве серийного типа изготовление деталей организуется по принципу партионности. Запускаемая в производство партия деталей может содержать от нескольких штук до тысяч деталей одного вида. После обработки одной партии станок переналаживается на изготовление деталей другого вида либо на другую технологическую операцию обработки тех же деталей.
      Из приведенной краткой характеристики машиностроительного производства следует, что основной задачей оперативно-календарного планирования (ОКП) производства серийного типа является задача построения календарного графика выпуска изделий. При известных технологических опережениях и известных применяемостях деталей в изделиях этот график определяет график изготовления различных деталей и сборочных единиц на производственных участках [1].
       При построении математической модели ОКП машиностроительного производства серийного типа примем следующие исходные предположения:
1) Размеры запускаемой в производство партии деталей устанавливаются исходя из условия точного укомплектования партии выпускаемых готовых изделий.
2) Технологические опережения слабо зависят от размеров запускаемых партий.
3) Производственные процессы периодически повторяются с периодом Т, где Т- число единичных временных интервалов (рабочих дней или смен) в периоде.
      Первое предположение соответствует распространенной методике ОКП – системе планирования серийной по опережениям [2]. При ней сводятся к минимуму размеры незавершенного производства. Второе предположение также в достаточной степени обосновано, поскольку в условиях серийного многономенклатурного производства время транспортировки и пролеживания составляет большую часть технологического опережения, до 80-90 процентов [3]. Третье предположение оказывается приемлемым в случае, когда условия производства (потребности в выпускаемых изделиях, производственные мощности и т.п.) не меняются или меняются медленно со временем.
      Постановка задачи. Пусть n – число видов изделий, l – число производственных участков. Из-за наличия технологических опережений выпуск одного изделия вида i в единичном интервале j создает загрузку b^ik_p участка k в единичном интервале (j-p), pE{0,1,2,…}. Выпуск изделий повторяется периодически с периодом Т. Суммарный выпуск изделий вида i в одном периоде должен быть равен aⁱ. Суммарная загрузка участка k в любом единичном интервале не должна превышать предельно допустимой загрузки b^k.
      При заданных целых положительных n, l, Т, aⁱ и положительных b^ik_p, b^k необходимо найти периодический график выпуска изделий, удовлетворяющий всем перечисленным условиям.
      Пусть xⁱ_j- искомое количество изделий вида i, планируемое к выпуску в единичном интервале j.Так как предполагается периодическая с периодом T повторяемость выпуска изделий, то вектор x=(x¹₀,...,x¹_T-1,...,xⁿ₀,...,xⁿ_T-1) однозначно определяет график выпуска и, согласно предположениям 1, 2, однозначно определяет график изготовления всех деталей и сборочных единиц на производственных участках.
       Условие точного выполнения плановых заданий (заказов) определяется уравнениями
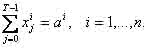      (1)

      Из исходных предположений следует, что трудоемкость обработки всех запускаемых в производство партий деталей и сборочных единиц в единичном интервале j для участка k равна

       Учитывая, что X_jⁱ=Xⁱ_j+T=Xⁱ_j+2T=..., последнюю формулу можно записать в виде
,
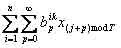       где (j+p)modT – остаток от деления (j+p) на Т. Положим
Q_t={p|pmodT=t, p=0,1,2,…}, t=0,1,…,T-1;

      Теперь ограничения на предельную загрузку производственных участков запишутся так:
 j=0,…,T-1; k=1,…,l.      (2)
      По своему содержательному смыслу переменные могут принимать только неотрицательные значения:
xⁱ_j≥0; j=0,…,T-1; i=1,…,n.      (3)
      Суммарные затраты на производство можно определить некоторой функцией f(x), где x=(x¹₀,...,x¹_T-1,...,xⁿ₀,...,xⁿ_T-1). С учетом свойств производства, в первую очередь с учетом затрат на переналадку, эта функция оказывается вогнутой. И тогда задача оптимизации календарного графика формулируется как задача определения
minf(x)      (4)
при условиях (1), (2), (3).
      Смысл оптимизации в данной задаче можно пояснить, если сказать, что допустимый вектор x^*, содержащий максимальное число нулевых компонент, либо является оптимальным, либо близким к оптимальному.
      Построенная математическая модель и задача (1)-(4) удовлетворяют основным принципам качественной модели. Во-первых, в модели отражены основные свойства производства. Во-вторых, модель пригодна как для крупносерийного, так и для мелкосерийного производства. Ее вид и размерность не зависят ни от параметров a¹,…,aⁿ, определяющих тип производства, ни от параметров b^ik_p, определяющих длительности циклов изготовления изделий. В-третьих, задача (1)-(4) является многоэкстремальной симметричной задачей с циклической группой симметрии порядка n. А для таких задач известен специальный алгоритм решения, основанный на свойстве симметрии [4].

1. Татевосов К. Г. Основы оперативно-производственного планирования на машиностроительном предприятии. – Л.: Машиностроение, 1985.
2. Смоляр Л. И. Модели оперативного планирования в машиностроительном производстве. – М.: Наука, 1978.
3. Беленький П. Е. Метод системного анализа в организации производственных процессов. – М.: Экономика, 1972.
4. Вьялицин А. А., Копаница С. В. Задачи минимизации вогнутых функций на симметричных многогранниках. – Петропавловск, Вестник СКУ, №1, 1997.