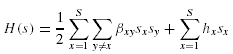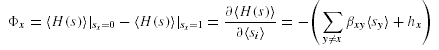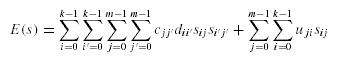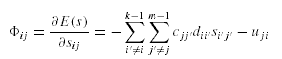Library

Evolutionary Algorithms for Allocating Data in Distributed Database Systems

Ishfaq Ahmad,Kamalakar Karlapalem
Source: http://ranger.uta.edu/~iahmad/journal-papers/[J39]%20Evolutionary%20algorithms%20for%20allocating%20data.pdf

Abstract

A major cost in executing queries in a distributed database system is the data transfer cost incurred in transferring relations (fragments) accessed by a query from different sites to the site where the query is initiated. The objective of a data allocation algorithm is to determine an assignment of fragments at different sites so as to minimize the total data transfer cost incurred in executing a set of queries. This is equivalent to minimizing the average query execution time, which is of primary importance in a wide class of distributed conventional as well as multimedia database systems. The data allocation problem, however, is NP-complete, and thus requires fast heuristics to generate efficient solutions. Furthermore, the optimal allocation of database objects highly depends on the query execution strategy employed by a distributed database system, and the given query execution strategy usually assumes an allocation of the fragments. We develop a site-independent fragment dependency graph representation to model the dependencies among the fragments accessed by a query, and use it to formulate and tackle data allocation problems for distributed database systems based on query-site and move-small query execution strategies. We have designed and evaluated evolutionary algorithms for data allocation for distributed database systems.


Keywords: data allocation, distributed database systems, query processing, optimal allocation, mean field annealing, genetic algorithm, simulated evolution, neighborhood search

1. Introduction

Distributed database systems have been a phenomenal success in terms of facilitating organization and processing of large volume of data. Distributed relational database technology is nearly two decades old and has developed the main ideas of maintaining consistency of distributed data and querying data. Recently, with the advent of multimedia and hypermedia data that are either too large and/or inherently distributed, handling distributed data becomes an issue of paramount importance. In a distributed database system, a query requires data to be accessed from one or more sites. The cost of executing the query depends on the location of the query as well as the data. Specifically, the data locality of a query determines the amount of data transfer incurred in processing the query; the higher the data locality the lower the data transfer costs. Thus, one is faced with the data allocation problem, the aim of which is to increase the data locality. Given a set of queries accessing a set of data fragments, a data allocation algorithm allocates these fragments to the sites of the distributed database system so as to minimize the total data transfer cost for processing the queries. In a distributed database system, a data fragment or simply fragment, corresponds to a relation or horizontal/vertical fragment of a relation, a multimedia data object like an audio file or video clip, or a hypermedia document like a web page. Hence, by using a generic notion of a fragment, we formulate the problem of data allocation, and develop algorithms that can solve the problem for specialized applications by incorporating the dependencies between query processing and data allocation.

Optimal allocation of fragments is, however, a complex problem as there exists a mutual interdependency between the allocation scheme (which gives the location of each of the fragments at various sites of a distributed database system) and the query optimization strategy (which decides howa query can be optimally executed given an allocation scheme). The fragment dependency graph models the dependencies between the fragments and the amount of data transfer incurred to execute a query. A fragment dependency graph (as shown in figure 1) is a rooted directed acyclic graph with the root as the query execution site (Site(Q) in figure 1) and all other nodes as fragment nodes (site(G), etc., in figure 1) at potential sites accessed by the query. A directed edge between one node to another is labelled with the amount of data transfer incurred if the fragments at these nodes are located at different sites. Note that the amount of data transferred (for example, size(G'')) depends on the query being processed and can be less than the size of the fragment accessed (that is, size(G'') < size(G)). The aim of a data allocation algorithm is to fix the sites where the fragments are located so as to minimize the total data transfer cost, under the storage constraints (i.e., the maximum number of fragments that can be allocated at a site) at each of the sites.



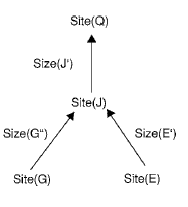
Figure 1. A fragment dependency graph (FDG).

A data allocation algorithm takes the following parameters as inputs: (I) the fragment dependency graphs, (II) unit data transfer costs between sites, (III) the allocation limit on the number of fragments that can be allocated at a site, and (IV) the query execution frequencies from the sites. The objective of this work is to design fast and efficient algorithms that can generate minimum total data transfer cost allocation schemes. We consider only nonredundant data allocation (i.e., each fragment is allocated to exactly one site). However, it should be noted that straightforward techniques are available for replicating the fragments in distributed database system [8] once a non-redundant allocation scheme is known.

Consider, for example, a distributed database system with four sites and two types of queries, as illustrated in figure 2. The network transportation costs and the query dependency graphs are shown in the figure. The problem is to allocate four data fragments to the four fully-connected sites such that the total data transfer cost for both the queries is minimized. Note that each query may have a different frequency of access at each site; that is, at some sites, a query may be invoked more frequently than at other sites. Thus, the total data transfer required for processing queries can be considerably different for various data allocation patterns. As will be shown subsequently, finding the best data allocation pattern is a complex problem even for small instances. Indeed, the data allocation problem for a distributed database system is known to be NP-complete in general [9, 11, 12, 19], and thus, optimal solutions cannot be found in a reasonable amount of time even for moderate sized problems. This objective of this paper is to introduce evolutionary and search-based heuristics for solving the data allocation problem aiming to obtain high quality solutions with fast turnaround times.

The rest of the paper is organized as follows: In the next section, we provide an overviewof previous work done in this area. Section 3 elaborates the data allocation problem. Section 4 introduces the algorithms proposed in this paper. Section 5 describes the environment for empirical evaluations for the proposed algorithms and presents the experimental results. Section 6 concludes the paper, and highlights some future research directions.


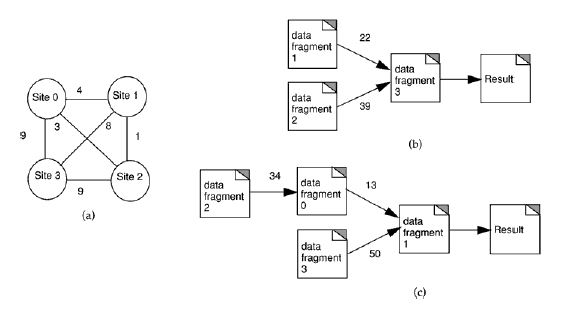
Figure 2. Distributed multimedia database network and data fragment dependency graphs for two queries. (a) A distributed database network. (b) The data fragment dependency graph for a query. (c) The data fragment dependency graph for another query.

2. Related work

Avariation of the data allocation problem has been studied in the context of the file allocation problem in a distributed computer system. The file allocation problem, however, does not take into consideration the semantics of the processing being done of files, whereas the data allocation problem must take into consideration the interdependencies among accesses to multiple fragments by a query. Chu [9] studied the problem of file allocation with respect to multiple files on a multiprocessor system, and presented a global optimization model to minimize overall processing costs under the constraints of response time and storage capacity with a fixed number of copies of each file. Casey [6] distinguished between updates and queries on files. Eswaran [11] proved that Casey’s formulation is NP-complete, and suggested an efficient heuristic.

Ramamoorthy and Wah [28] analyzed a file allocation problem in the environment of a distributed database and developed an approximate algorithm for a simple file allocation problem and a generalized file allocation problem. Ceri et al. [7] considered the problem of file allocation for typical distributed database applications with a simple model for transaction execution taking into account the dependencies between accesses to multiple fragments. Frieder and Siegelmann [12] have recently suggested a proof that the multiprocessor document allocation (MDAP) problem is NP-complete. In their MDAP formulation, they assume that there are a number of distinct documents, which are agglomerated into several clusters, to be allocated to a number of homogeneous processors. The MDAP problem is reduced to the binary Quadratic Assignment Problem (an NP-complete problem [13]) in polynomial time. Frieder and Siegelmann then proposed a simple genetic algorithm to solve the problem heuristically. It should be noted that theMDAP problem does not consider the query structures of accessing the documents; whereas in the present paper, the queries are modeled as directed data transfer graphs which play a vital role in the data allocation problem considered.

Apers [1] considered the allocation of the distributed database to the sites so as to minimize total data transfer cost, and devised a complicated approach to allocate relations by first partitioning them into innumerable number of fragments, and then allocating them. Apers did integrate the system dependent query processing strategy with the logical model for allocating the fragments. But the drawback is that the fragmentation and allocation problems are addressed together. That is, the fragmentation schema must be one of the outputs of the allocation algorithm. This curtails the applicability of this methodology when fragmentation schema is already defined and allocation scheme must be generated.

Cornell and Yu [10] proposed a strategy to integrate the treatment of relation assignment and query strategy to optimize performance of a distributed database system. Even though they took into consideration the query execution strategy, their linear programming solution is rather complicated. Another problem in their approach is the lack of simplicity in both the incorporation of the query execution strategy and the solution procedure. A few other linear programming formulations have also been proposed for the data allocation problem [14, 27]. The main problem with these approaches is the lack of modeling of the query execution strategy. Lin et al. [15] developed a heuristic algorithm for minimum overall data transfer cost, by considering replicated allocation of fragments and both read and update transactions.

In [18] and [19], we developed a framework for query driven data allocation algorithms in the context of both distributed multimedia database systems and distributed relational database systems. The goal was to evaluate the effectiveness of the hill-climbing data allocation algorithm for two specific query execution strategies, namely, move-small and query-site. In this paper, we develop an uniform framework for modeling data allocation problem, and facilitate generic solutions to this problem. Further, we present an exhaustive study of evolutionary data allocation algorithms concentrating on quality of solution, time and space complexity. In particular, we have proposed four different algorithms, each based on different heuristics, and evaluate their results by comparing against the optimal exhaustive enumeration solution.

3. The data allocation problem

In this section, we discuss in detail the data allocation problem and characterize the underlying distributed multimedia database system. Table 1 summarizes the key notations used in our discussion.

Consider a distributed database system with m sites, with each site having its own processing power, memory, and a local database system. Let Si be the name of site i where 0<=i<=m-1. The m sites of the distributed multimedia database system are connected by a communication network. A link between two sites Si and Si' (if it exists) has a positive integer cii' associated with it representing the cost for a unit data transferred from site Si to site Si'. If two sites are not directly connected by a communication link then the cost for unit data transferred is given by the sum of the cost of links of a chosen path from site Si to site Si'. Let Q ={q0, q1, . . . , qn-1} be the most important queries accounting for say more than 80% of the processing in the distributed database system. Each query qx can be executed from any site with a certain frequency. Let aix be the frequency with which query qx is executed from site Si. The execution frequencies of n queries at m sites can be represented by a m*n matrix, A. Let there be k data fragments, named {O0, O1, . . . , Ok-1}.

Table 1. Definitions of notations.


3.1. Query representation

The data allocation problem is difficult because of the mutual interdependency between the query execution strategy (decided by the query optimizer) and the allocation of the fragments. The optimal allocation of the fragments depends on a given query execution strategy and the optimal query execution strategy depends on a fixed materialization of the fragments (i.e., fixing the location of the fragments accessed by the query). The main problem in deciding on the optimal allocation is the lack of a representational model of the dependencies among the fragments accessed by the query. These dependencies arise because of the partitioning of the relations into fragments and/or access to multiple relations by a query. We use the distributed query decomposer and data localization algorithms [22] to decompose a distributed query into a set of fragment queries. This decomposed query incorporates the dependencies between fragments. These dependencies model binary operations (like join, union) between the fragments that need to be processed in order to execute the distributed query. We estimate the sizes of the intermediate relations generated after executing the unary and binary operations by making use of the database statistics (like, cardinality and lengths of tuples of the fragments/relations) available from the system catalog. Since we are incorporating distributed query processing, the query decomposition and data localization phases eliminate access to irrelevant fragments and generate a concise decomposed query operator trees on fragments. In the distributed query optimization and execution phase optimal binary operation orderings are based on a query execution strategy.
A query execution strategy can be:

  1. Move-Small: If a binary operation involves two data fragments located at two different sites then ship the smaller data fragment to the site of the larger data fragment.

  2. Query-Site: Ship all the data fragments to the site of query origin and execute the query.

Note that the objective of data allocation is to minimize the total data transfer cost to process all the queries by using one of the above query execution strategies. The first aim of data allocation is to maximize the locality of the fragments for executing the queries. The second aim is to incorporate the query execution strategy when a query needs to access fragments from multiple sites and reduce the total data transfer cost to process all the queries.

3.2. The data transfer cost model

The data fragment dependency graph of every query models two types of data transfer cost. The first type of cost is due to moving the data from the sites where the data fragments are located to the site where the query is initiated. The second type of cost is due to moving the data from the site where one data fragment is located to the site where another data fragment is located. In this case, the size of the data fragment required by every site does not vary with the location of other data fragments as there is no dependency between the data fragments accessed by the query. This is true in the case of query-site query processing strategy, and the top level of the data fragment dependency graphs.

Let rxj be defined as the size of data of data fragment Oj needed to be transported to the site where qx is initiated. The corresponding matrix is R of size n*k. Note that this incorporates the top level of the data fragments dependency graph. Let there be a query qx initiated from site Si, aix times in an unit time interval. Let U be a m*k matrix where uij gives the amount of data needed to be transferred from the site where data fragment Oj is allocated to the site Si where the queries are initiated. That is,

And in matrix representation,U = A*R

The second type of data transfer cost corresponds to the deeper levels of the data fragments dependency graph. The data is transported from the site where one data fragment is located to the site where the other data fragment is located in order to perform binary operation involving two (or more) different data fragments. In this case, the amount of data of a data fragment required by a site varies with the allocation of other data fragments. Let djj' define the size of data from data fragment Oj that needs to be transported to the site where Oj' is located so as to execute some binary operation. Let the corresponding matrix, k*k, be D. But this is dependent on the query that is to be processed. Therefore, for each query we need to extract the information about how much data needs to be transferred from site where one data fragment is located to the site where another data fragment is located given that both the data fragments are accessed by the query. This information is extracted by the data fragments dependency graph generator which processes the query operator trees on data fragments by applying a query execution strategy and is represented in the data fragment dependency graph.

Let dxjj' be the data size of Oj needed to be transported to the site where Oj' is located to process qx . And let the corresponding matrix be Dx . Then the amount of data that needs to be transported from the site where Oj is located to the site where Oj' is given by:



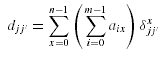
And in matrix representation,



Let site(Oj) denote the site where data fragment Oj is located. Then, the total transportation cost, t, is given by:



where the first term gives the data transfer cost incurred to process the binary operations between the data fragments located at different sites, and the second term gives the data transfer cost incurred to transfer the results of the binary operations of data fragments to the site where the query is initiated. The objective in data allocation problem is to minimize t by altering the function site(Oj) (which maps a data fragment to a site).

To illustrate, let us consider the scenario shown earlier in figure 2 in which four data fragments are to be allocated to a four-site network given that there are two queries. The access frequencies of the query 0 and query 1 for the four sites are given by:


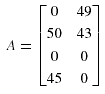
Thus, the total access frequencies of each query are 95 and 92, respectively, and hence the data fragment dependency cost matrix is given by:

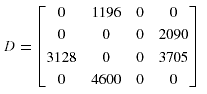
Suppose that the query data transfer size matrix is given by:

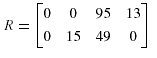
Thus, the data fragment allocation cost matrix is then given by:

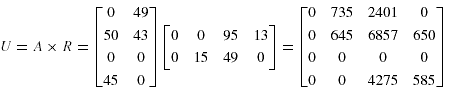
4. Proposed data allocation algorithms

The data allocation problem is NP-complete in general [11] and thus requires heuristics that are fast and are capable of generating high-quality solutions. Developing an efficient heuristic highly depends on the query execution strategy employed by the distributed database system. This is because different query execution strategies have different data fragment migration patterns. We develop solutions for the data allocation problem when query-site and move-small query execution strategies are respectively used by the distributed database management system and the multimedia data provider.

We propose four heuristics on search techniques that have shown considerable potential in solving a wide range of other optimization problems [24, 30]. The first algorithm is based upon a traditional genetic algorithm. The second algorithm is based upon simulated evolution technique, which, as opposed to traditional genetic algorithms, relies on crossover and encode the information in the solution domain. Furthermore, the simulated evolution algorithm uses mutation as the primary search mechanism and encode information in the problem domain. The third algorithm is based upon a technique that is a combination of neural networks and simulated annealing. The fourth algorithm is based upon a random search technique. These algorithms are described as follows.



4.1. The genetic algorithm

Genetic algorithm (GA) based search methods [16, 17, 21, 30] are inspired by the mechanisms of natural genetics leading to the survival of the fittest individuals. Genetic algorithms manipulate a population of potential solutions to an optimization problem [30]. Specifically, they operate on encoded representations of the solutions, equivalent to the genetic material of individuals in nature, and not directly on the solutions themselves. In the simplest form, solutions in the population are encoded as binary strings. As in nature, the selection mechanism provides the necessary driving force for better solutions to survive. Each solution is associated with a fitness value that reflects how good it is, compared with other solutions in the population. The higher the fitness value of an individual, the higher the chance of survival in the subsequent generation. Recombination of genetic material in genetic algorithms is simulated through a crossover mechanism that exchanges portions between strings. Another operation, called mutation, causes sporadic and random alternation of the bits of strings. Mutation also has a direct analogy with nature and plays the role of regenerating lost genetic material.

In the proposed genetic algorithm for the data allocation problem, we encode the assignment of each data fragment in a binary representation. For example, if a data fragment is assigned to site 3, then its assignment value is 11. The assignment value of all the data fragments are concatenated to form a binary string. Each binary string then represents a potential solution to the data allocation problem. The fitness of the string is simply the cost of the allocation. The selection mechanism is implemented as a simple proportionate selection scheme: a string with fitness f is allocated f /(f') offspring, where f' is the average fitness value of the population. A string with a fitness value higher than the average is allocated more than one offspring, while a string with a fitness value lower than the average is allocated less than one offspring.

Crossover is another crucial operation of a GA. Pairs of strings are picked at random from the population to be subjected to crossover. We use the simple single point crossover approach. Assuming that L is the string length, the algorithm randomly chooses a crossover point that can assume values in the range 1 to L - 1. The portions of the two strings beyond this crossover point are exchanged to form two new strings. The crossover point may assume any of the L - 1 possible values with equal probability. Note that crossover is performed only when a randomly generated number in the range is greater than a prespecified crossover rate pc (also called the probability of crossover); otherwise, the strings remain unaltered. The value of pc lies in the range from 0 to 1. In a large population, pc gives the fraction of strings actually crossed.

After crossover, strings are subjected to mutation. Mutation of a bit is to flip a bit. Just as pc controls the probability of a crossover, another parameter, pc (the mutation rate), gives the probability that a bit will be flipped. The bits of a string are independently mutated. That is, the mutation of a bit does not affect the probability of mutation of other bits. Mutation is treated as a secondary operator with the role of restoring lost genetic material. The genetic algorithm for the data allocation problem is described below.

Genetic Data Allocation Algorithm:
(1) Initialize population. Each individual of the population is a concatenation of the binary representations of the initial random allocation of each data fragment.
(2) Evaluate population.
(3) no-of-generation = 0.
(4) WHILE no-of-generation < MAX-GENERATION DO.
(5)       Select individuals for next population.
(6)       Perform crossover and mutation for the selected individuals.
(7)       Evaluate population.
(8)       no of generation ++;
(9) ENDWHILE
(10) Determine final allocation by selecting the fittest individual. If the final allocation is not feasible, then consider each over-allocated site to migrate the data fragments to other sites so that the increase in cost is the minimum.

The time complexity of the GA allocation approach is O(GNp(k2 + km)), where G is the number of generations and Np is the population size.

For the small allocation problem shown eariler in figure 2, the initial chromosome of the GA is depicted in figure 3(a). After the iterative applications of the genetic operators, the final solution is represented by the chromosome shown in figure 3(b), which represents the allocation: data fragment 0 to site 2, data fragment 1 to site 1, data fragment 2 to site 1, and data fragment 3 to site 2. The total allocation cost is 67,378. The time taken using a Sun Ultra workstation is 474 seconds.

a)  (10   11   00   01)       b)  (10   01   01   10)
Figure 3. The initial and final chromosomes of the GA. (a) Initial chromosome and (b) Final chromosome.

4.2. The simulated evolution algorithm

This variant of the traditional genetic algorithm is called problem-space simulated evolution [18, 19]. Simulated annealing, genetic algorithms, and evolutionary strategies are similar in their use of probabilistic search mechanism directed toward decreasing or increasing an objective cost function. These three methods have a high probability of locating the global solution optimally in a search profile, despite that a multimedia cost function has several locally optimal solutions. However, each method has a significantly different mode of operation: Simulated annealing probabilistically generates a sequence of states based on a cooling schedule to ultimately converge to the global optimum. Evolutionary strategies use mutations as search mechanisms and selection to direct the search toward the prospective regions in the search space. Genetic algorithms generate a sequence of populations by using a selection mechanism, and use crossover and mutation as search mechanisms.

The principal difference between a genetic algorithm and an evolutionary strategy is that the former relies on crossover, a mechanism of probabilistic, and useful exchange of information among solutions to locate better solutions, while the latter uses mutation as the primary search mechanism. Furthermore, in the proposed scheme the chromosomal representation is based on problem data, and solution is generated by applying a fast decoding heuristic (mapping heuristic) in order to map from problem domain to solution domain. The generic problem-space simulated evolution is as below.
Simulated Evolution Data Allocation Algorithm:
(1) Construct the first chromosome based on the problem data and perturb this chromosome to generate an initial population;
(2) Use the mapping heuristic to generate a solution for each chromosome;
(3) Evaluate the solutions obtained;
(4) no-of-generations = 0;
(5) WHILE no-of-generations < MAX-GENERATION DO
(6)       Select chromosomes for next population;
(7)       Perform crossover and mutation for these set of chromosomes;
(8)       Use the mapping heuristic to generate a solution for each chromosome;
(9)       Evaluate the solutions obtained;
(10)      no-of-generations = no-of-generations+1;
(11) ENDWHILE
(12) Output the best solution found so far.

Chromosomes: The chromosome structure is as follows:

where the number of genes in a = total limit, and number of genes in b = total number of fragments.

For a, each gene is a single bit. A value of 1 indicates that the corresponding allocation space is allowed to be used for this chromosome. Otherwise, if the bit is 0, the space cannot be used. This reduces the effective allocation limit for each sites. For b, each gene is an integer which represents the priority of the fragment to be considered; a large value means high priority and a small value means low priority.

Using the network transportation cost matrix C, query access frequencies and the data transfer sizes, we can compute a data fragment-site allocation cost matrix, denoted by U', which is given by: U' = C * U

That is, each entry of U', denoted by u'ij, represents the site allocation cost incurred if data fragment j is allocated to site i>.For the allocation example shown in figure 2, U' is given by:

In the Simulated Evolution algorithm, the first chromosome in the initial population is constructed from the information of the table of u'ij which, as mentioned above, represents the cost of allocating fragment j to site i . For each fragment j, we calculate
The purpose is to minimize the allocation cost by giving a higher priority to the fragment with larger Xj (a large value of Xj means that this fragment will use more transmission time (cost)). Thus, we simply assign Xj as the genes for each fragment position in part b of the first chromosome in the initial population.

All of the genes in part a of the chromosomes are set to 1 for the first chromosome in the initial population since this is the allocation limit of the original problem. For the remaining chromosomes in the initial population, the genes in a are chosen randomly as 0 or 1. The genes in b are perturbations of the first chromosome’s corresponding genes in b. Notice that for genes in a, we must check whether the new effective allocation limit is enough for all fragment to be allocated. This can be done simply by counting the number of 1’s in a and by checking that this sum is greater than or equal to the total number of fragments k.

Mapping heuristic: For each chromosome, we find a solution by allocating fragment j with the highest priority to the site i such that u'ij is smallest for all u'xj, 1<x<m. If the effective allocation limit embedded in the genes in part a of the chromosome for that site is exceeded (the site is already saturated), we allocate this fragment to the site with the next smallest value of u'ij for all u'yj, 1&ly&lm, y <>x x. It is guaranteed that the fragment can be allocated to some site since we have checked that the total allocation limit is greater than or equal to the total number of fragments for every generation of chromosome. We then continue the process for the next fragment with the highest priority among fragments not yet allocated.

Cost and fitness function: For each chromosome, the cost function is the total transmission cost after allocating all the fragments to some site using the mapping heuristic. The calculation of this transmission cost will consider both fragment dependencies and fragment sizes needed by each site. The fitness value for the chromosome is calculated as

where Np is population size, MaxCost is the maximum cost among the chromosomes in the population, and tau is the convergence factor used for controlling the rate of convergence.

Genetic operators: The two genetic operators are selection and crossover. To illustrate these, let the two chromosomes under the crossover operator be c1 and c2. Assume that the cutting position is at z, that is,

c1:c11c12      and      c2:c21c22

where number of genes in c11 and c21 are z. Then the two new chromosomes after the crossover are,

c'1:c12c12      and       c'21c22

For genes in a, mutation sets the value to either 1 or 0. For genes in b, perturbing the value in the gene by adding a randomly chosen value from -n to m (n and m are set as the maximal value of b-genes divided by 4 in this chromosome. We must check the validity of the effective allocation limit for each chromosome here also (i.e., the sum of 1’s for genes in a>=k, the number of fragments).

Unlike the previous algorithm, there is no need for checking the validity of the final solution since we explicitly encode the information of allocation limits in the chromosomes and ensure that these limits will not excess for all solution obtained. The time complexity of the problem-space simulated evolution algorithm, like the GA, is O(GP(k22+km)), where G is the number of generations and P is the population size.

For the allocation example shown in figure 2, the initial chromosome of the SE algorithm is depicted in figure 4. Similar to the GA, with the iterative application of crossover, mutation and selection, the final solution converges to the allocation: data fragment 0 to site 1, data fragment 1 to site 2, data fragment 2 to site 1 and data fragment 3 to site 2. The total allocation cost of this solution is equal to 57,470, which is the optimal cost. The time taken is only 79 seconds.


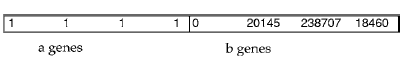
Figure 4. The initial chromosome of the SE algorithm.

4.3. The mean field annealing algorithm

Mean field annealing (MFA) technique [3, 5, 25] combines the collective computation property of the famous Hopfield Neural Network (HNN) with simulated annealing [32]. MFA was originally proposed for solving the travelling salesperson problem, as an alternative to HNN, which does not scale well for large problem sizes. It has been shown that MFA is a general approach [3, 4] that can be applied to various combinatorial optimization problems.

We first describe the general formulation of MFA [3]. The MFA algorithm is derived from an analogy to the Ising spin model which is used to estimate the state of a system of particles or spins in thermal equilibrium. In the Ising spin model, the energy of a system with S spins has the following form:

where bxy represents the level of interaction between spins x and y, and sx = {1, 0} is the value of spin x. It is assumed that bxy = bxy and bxx = 0 for 1<=x, y<=S. At the thermal equilibrium, spin average <sx> of spin x can be calculated using Boltzmann distribution as follows:

where Ôx = <sH(s)>|sx=0 - <H(s)>|sx=1 represents the mean field acting on spin x, where the energy average <sH(s)> of the system is:

The complexity of computing Ôx using the above equation is exponential. However, for large number of spins, the mean field approximation can be used to compute the energy average as:

Hence <sH(s)> is linear in <ssx>, the mean field Ôx can be computed using the equation:
Thus, the complexity of computing Ôx reduces to O(S).

At each temperature, starting with initial spin averages, the mean field Ôx acting on a randomly selected spin is computed. Then the spin average is updated. This process is repeated for a random sequence of spins until the system is stabilized for the current temperature. The generic MFA algorithm is described as follows:
(1) Get the initial temperature T0, set T = T0.
(2) Initialize the spin averages <ss> = [<ss1>, . . . , <sss>].
(3) WHILE temperature T is in the cooling range DO
(4)    WHILE system is not stabilized for the current temperature DO
(5)      Select a spin x at random.
(6)      Compute Ôx .
(7)      Update <ssx>
(8)    ENDWHILE
(9)    Update T according to the cooling schedule.
(10) ENDWHILE

We formulate the data allocation problem as MFA in the following manner. Instead of a linear spin array, a spin matrix (sij) is used to encode the allocation of the data fragments to sites. The matrix consists of x rows and m columns, representing x data fragments and m sites, respectively. A value of 1 in each entry indicates the data fragment is allocated to the corresponding site. For example, if ssij = 1, then data fragment i is allocated to site j . A valid allocation is one in which each row of the spin matrix has exactly a single 1. Each spin variable is a continuous variable in the range [0, 1]. Spin values converge to either 1 or 0 at the fixed point. Given this formulation, the energy function (i.e., the data transfer cost function) for the data allocation problem can be formalized as described below.

Using the mean field approximation, the expression for the mean field Ôij experienced by spin sij is:

In a feasible allocation, each data fragment should be allocated to exclusively one site. Thus, the sum of the spins across each row of the matrix should equal unity. This constraint can be explicitly handled while updating by normalizing each spin sij as:
Given the above formulation, the MFA algorithm to solving the data allocation problem can be briefly formalized below.
MFA Data Allocation Algorithm:
(1) Get the initial temperature T0, set T = T0.
(2) Initialize the spin averages s = [s00,s01, . . . , sk-1,m-1] each sij is initialized as a random number between 0 and 1.
(3) WHILE temperature T is in the cooling range DO
(4)    WHILE E is decreasing DO
(5)       Select a data fragment i at random.
(6)       Compute the mean field of the spins at the i-th row, i.e., Ôij
(7)       Compute the summation
(8)       Compute the new spin values at the i-th row.
(9)       Compute the energy change due to these updates.
(10)   ENDWHILE
(11)    Update the temperature T according to the cooling schedule.
(12) ENDWHILE
(13) Determine the final allocation by allocating each data fragment to the site with the largest spin value. If the final allocation is not feasible, then consider each overallocated site to migrate the data fragments to other sites so that the increase in cost is the minimum.

Note that the last step of the MFA algorithm is necessary because we do not explicitly check for feasibility in the search process, which can then explore a broader regions in the search space. However, we found that this adjustment of the final allocation was seldom invoked as the allocation limits were usually very loose. The time complexity of a single iteration of the inner WHILE-loop is O(k(k + m)). Using a linear cooling schedule with k temperature values and assuming a bound B on the number of iterations of the inner WHILE-loop, the overall time complexity of the MFA algorithm is O(BK(k2 + km)).

For the example allocation problem in figure 2, the matrix below shows the initial spin values of the MFA algorithm:

which represents allocating data fragment 0 to site 0, data fragment 1 to site 2, data fragment 2 to site 1 and data fragment 3 to site 0. After a number of iterations, the spin values evolve to the final allocation as shown below:

which represents allocating data fragment 0 to site 2, data fragment 1 to site 1, data fragment 2 to site 1 and data fragment 3 to site 2. This allocation is the same as that of the GA and the total allocation cost of this solution is equal to 67,378. The time taken is 11 seconds.

4.4. Random neighborhood search data allocation algorithm

We employ a low complexity but effective optimization technique known as random neighborhood search [24]. The main idea in a neighborhood search algorithm is to generate an initial solution with moderate quality. Then, according to some pre-defined neighborhood, the algorithm probabilistically selects and tests whether a nearby solution in the search space is better or not. If the new solution is better, the algorithm adopts it and starts searching in the new neighborhood; otherwise, the algorithm selects another solution point. The algorithm stops after a specified number of search steps has elapsed or the solution does not improve after a fixed number of steps. The solution quality of a neighborhood search technique relies heavily on the construction of the solution neighborhood. The algorithm for the data allocation problem is given as follows:
Random Search (RS) Algorithm:
(1)Use Divisive-Clustering [19] to find an initial allocation Initial-Alloc;
(2) Best-Alloc = Initial-Alloc;
(3) New-Alloc = Best-Alloc; iteration = 0; REPEAT (4)    searchstep = 0; counter = 0;
   REPEAT
(5)       Randomly select two sites from New-Alloc;
(6)       Randomly select two data fragments from each site;
(7)       Exchange the two data fragments;
(8)       IF cost is reduced THEN
       adopt the exchange and set counter to 0;
       ELSE otherwise undo it and increment counter;
   UNTIL ++searchstep > MAXSTEP OR counter > MARGIN;
(9)    IF cost(New-Alloc) < cost(Best-Alloc) THEN Best-Alloc = New-Alloc;
(10)   Randomly exchange two data fragments from two randomly selected distinct sites from New Alloc; /* Probabilistic jump */
UNTIL iteration > MAXITERATION;

For the example problem in figure 2, the allocation generated by the RS algorithm is: data fragment 0 to site 1, data fragment 1 to site 2, data fragment 2 to site 2 and data fragment 3 to site 2. The total allocation cost of this solution is 65,624. The time taken is 31 seconds. From the small allocation example depicted in figure 2, we can see that the SE algorithm generates the best (optimal) solution but takes moderately long time to terminate. The MFA algorithm is the fastest but its solution quality is not satisfactory. Similar argument applies to the RS algorithm. The GA performs the worst in that its solution quality is inferior and it takes the longest time to terminate.

5. Experimental results

To understand the merits and demerits of the four proposed data allocation algorithms, we present the results of our experiments. Comparisons are made with respect to the solution quality and the algorithm’s running time. For comparison, we obtained optimal solutions using an exhaustive search.We applied the algorithms to the configurations showninTable 2.

For each configuration, we generated 100 different problem instances by random construction of the query graphs and random selection of number of queries from a uniform distribution with range [10, 20]. Thus, the total number of problem instances is 4,100. Since the values of the data fragment sizes critically affect the quality of the final allocation [19], we tested the algorithms with six different mean values of data fragment sizes. We first fixed the mean network transfer cost to be 10 units of data per unit time (with range [1, 20]). Then we generated six mean data fragment sizes by multiplying the mean network transfer cost by six cost ratio: 1, 5, 25, 100, 250, and 500 (the ranges were also multiplied by the same factors). Both the network transfer costs and the data fragment sizes were generated from uniform distributions. Consequently, the total number of test cases were 24,600.

The average degradations from optimal solutions for the four algorithms are shown in Table 3. One immediate observation is that all the algorithms perform better for larger cost ratios. This is because if the data fragment sizes are comparable to the network speed, the response time becomes very sensitive to the placement of the data fragments onto the sites. On the other hand, if the data fragment sizes are much larger than the network speed, the response time will not be affected much by the allocation but will rather by affected by the dependency of the data fragments in the query graphs. For small cost ratios, the SE algorithm performed better than the other three algorithms. However, when the effect of cost ratio saturated (at ratio = 100), the GA outperformed the others. MFA was worse than RS for small ratios but performed better for large ratios.

Table 2. Configurations of test cases.

Table 3. Average % degradation from optimal of the four data allocation algorithms for various cost ratios.

6. Conclusions

In this paper, we address the problem of non-redundant data allocation of fragments in distributed database system. We have developed a query driven data allocation approach integrating the query execution strategy with the formulation of the data allocation problem. We have also proposed various algorithms, designed based on the evolutionary computing paradigm, for the data allocation problem in distributed database systems. A major contribution of this work is the development of a site-independent fragment dependency graph representation of data transfer costs incurred in executing a query by using a particular query execution strategy. This enables the application of query driven allocation approach to allocate database objects under different database systems (like, relational, object-oriented, network, etc.) and facilitates the development of an uniform framework within which to define and solve data allocation problems.

In our extensive experimental studies, we have evaluated and compared the four proposed data allocation heuristics, including a genetic algorithm (GA), a simulated evolution (SE) algorithm, a mean field annealing (MFA) algorithm, and a random search (RS) algorithm, in terms of query response time and algorithm running time. An interesting conclusion is that no single algorithm outperforms all others in both aspects. The SE and GA can generate better solutions than RS and MFA in general. However, the difference in solution quality is not always of the same magnitude. Also, the RS algorithm has the lowest time complexity which makes it the fastest algorithm, whereas the SE algorithm is quite slow. For fast running time and a small degradation of the optimality of the solution, the RS algorithm is a viable choice. On the other hand, when efficiency and solution quality are equally important, the GA may be a more attractive choice. Thus, the advantage of having these algorithms in a distributed database is the availability of a diverse range of solution quality and complexity trade-off.

References

  1. P.M.G. Apers, “Data allocation in distributed database systems,” ACM Transactions on Database Systems, vol. 13, no. 3, pp. 263–304, 1988.
  2. P.B. Berra, C.Y.R. Chen, A. Ghafoor, C.C. Lin, T.D.C. Little, and D. Shin, “Architecture for distributed multimedia systems,” Computer Communications, vol. 13, no. 4, pp. 217–231, 1990.
  3. D.E. Van den Bout and T.K. Miller, “Graph partitioning using annealed neural networks,” IEEE Transactions on Neural Networks, vol. 1, no. 2, pp. 192–203, 1990.
  4. D.E. Van den Bout and T.K. Miller, “Improving the performance of the Hopfield-Tank neural network through normalization and annealing,” Bio. Cybernet, vol. 62, pp. 129–139, 1989.
  5. T. Bultan and C. Aykanat, “A new mapping heuristic based on mean field annealing,” Journal of Parallel and Distributed Computing, vol. 16, pp. 292–305, 1992.
  6. R.G. Casey, “Allocation of copies of a file in an information network,” in Proceedings of the Spring Joint Computer Conference, IFIPS, July 1972, pp. 617–625.
  7. S. Ceri, G. Martella, and G. Pelagatti, ‘Optimal file allocation for a distributed on a network of minicomputers,” in Proceedings of the International Conference on Databases, July 1980, pp. 345–357.
  8. S. Ceri and G. Pelagatti, Distributed Databases: Principles and Systems, McGraw Hill: New York, 1984.
  9. W.W. Chu, “Optimal file allocation in a multiple computer system,” IEEE Transactions on Computers, vol. C-18, no. 10, 1969.
  10. D.W. Cornell and P.S. Yu, “Site assignment for relations and join operations in the distributed transaction processing environment,” in Proceedings of the IEEE International Conference on Data Engineering, Feb. 1988.
  11. K.P. Eswaran, “Placement of records in a file and file allocation in a computer network,” Information Processing, 1974, pp. 304–307.
  12. O. Frieder and H.T. Siegelmann, “Multiprocessor document allocation: A genetic algorithm approach,” IEEE Transactions on Knowledge and Data Engineering, vol. 9, no. 4, pp. 640–642, 1997.
  13. M.R. Garey and D.S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness, Freeman: New York, 1979.
  14. B.Gavish and H. Pirkul, “Computer and database location in distributed computer systems,” IEEETransactions on Computers, vol. C-35, no. 7, pp. 583–590, 1986.
  15. A. Ghafoor, “Multimedia database management systems,” ACMComputing Surveys, vol. 27, no. 4, pp. 593– 598, 1995.
  16. D.E. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning, Addison-Wesley: Reading, MA, 1989.
  17. S. Hurley, “Taskgraph mapping using a genetic algorithm: A comparison of fitness functions,” Parallel Computing, vol. 19, pp. 1313–1317, 1993.
  18. K. Karlapalem and M.-P. Ng, “Query-driven data allocation for distributed database systems,” in Proceedings of 8th International Conference on Database and Expert Systems Applications, Sept. 1997, pp. 347– 356.
  19. Y.-K. Kwok, K. Karlapalem, I. Ahmad, and M.-P. Ng, “Design and evaluation of data allocation algorithms for distributed multimedia database systems,” IEEE Journal on Selected Areas in Communications, vol 14, no. 7, pp 1332–1348, 1996.
  20. T.D.C. Little and A. Ghafoor, “Synchronization and storage models for multimedia objects,” IEEE Journal on Selected Areas in Communications, vol. 8, no. 3, pp. 413–427, 1990.
  21. S.W. Mahfoud and D.E. Goldberg, “Parallel recombinative simulated annealing:Agenetic algorithm,” Parallel Computing, vol. 21, pp. 1–28, 1995.
  22. T. Ozsu and P. Valduriez, Principles of Database Systems, Prentice-Hall: Englewood Cliff, NJ, 1991.
  23. M.T. Ozsu, D. Szafron, G. El-Medani, and C. Vittal, “An object-oriented multimedia database system for a news-on-demand application,” Multimedia Systems, vol. 3, no. 5/6, 1995.
  24. C.H. Papadimitriou and K. Steiglitz, Combinatorial Optimization: Algorithms and Complexity, Prentice-Hall: Englewood Cliffs, NJ, 1982.
  25. C. Peterson and B. Soderberg, “A new method for mapping optimization problems onto neural networks,” International Journal of Neural Systems, vol. 1, no. 3, 1989.
  26. T.C. Rakow, E.J. Neuhold, and M. Lohr, “Multimedia database systems: The notions and the issues,” in Tagungsband GI-Fachtagung Datenbanksystems, Buro, Technik and Wissenschaft (BTW), Dresden Marz 1995, Springer Informatik Aktuell, Berlin, 1995.
  27. S. Ram and R.E. Marsten, “A model for database allocation incorporating a concurrency control mechanism,” IEEE Transactions on Knowledge and Data Engineering, vol. 3, no. 3, pp. 389–395, 1991.
  28. C.V. Ramamoorthy and B.Wah, “The placement of relations on a distributed relational database,” in Proceedings of the 1st International Conference on Distributed Computing Systems, Oct. 1979, pp. 642–649.
  29. P.I. Rivera-Vega, R. Varadarjan, and S.B. Navathe, “Scheduling data redistribution in distributed databases,” in Proceedings of the IEEE International Conference on Data Engineering, Feb. 1990.
  30. M. Srinivas and L.M. Patnaik, “Genetic algorithms: A survey,” Computer, vol. 27, no. 6, pp. 17–26, 1994.
  31. B.Wilson and S.B. Navathe, “An analytical framework for the redesign of distributed databases,” in Proceedings of the 6th Advanced Database Symposium, 1986.
  32. L. Yong, K. Lishan, and D.J. Evans, “The annealing evolution algorithm as function optimizer,” Parallel Computing, vol. 21, pp. 389–400, 1995.

      33.