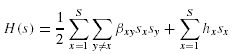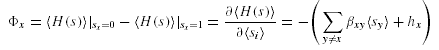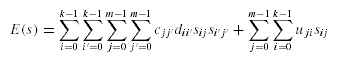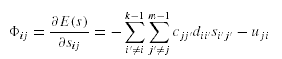В библиотеку

Эволюционные алгоритмы в задачах размещения данных в распределенных базах данных

Ishfaq Ahmad,Kamalakar Karlapalem
Источник: http://ranger.uta.edu/~iahmad/journal-papers/[J39]%20Evolutionary%20algorithms%20for%20allocating%20data.pdf
Перевод Барановой С.С.

Аннотация

Главные затраты в выполнении запросов в системе распределенной базы данных - это затраты на передачу данных, вытекающая из переноса отноше-ний (фрагментов), доступных запросу от различных узлов к узлу, где запрос инициирован. Задача алгоритма размещения данных - определить размещение фрагментов на различных узлах, чтобы минимизировать общую стоимость передачи данных, возникающую при выполнении набора запросов. Это равноценно минимизации среднего времени выполнения запроса, которая имеет первоначальную важность в широком классе как стандартных РБД, также как и систем мультимедийной базы данных. Проблема размещения данных, NP-полная, и поэтому требует быстрых эвристик, чтобы генерировать эффективные решения. К тому же, оптимальное размещение объектов базы данных сильно зависит от стратегии выполнения запроса, используе-мой системой распределенной базы данных, и предоставленная стратегия выполнения запроса обычно принимает на себя размещение фрагментов. Мы разрабатываем независимое от узла представлеение графа зависимости фрагментов, доступных запросу, чтобы сформулировать проблемы размещения данных для РБД, основанных на стратегии выполнения запроса query-site и move-small. Мы разработали и оцененили эволюционные алгоритмы для размещения данных для РБД.


Ключевые слова: распределение данных, распределенная база данных, выполнение запроса, оптимальное распределение, генетический алгоритм, симуляция эволюции.

1. Введение

Распределенные базы данных получили широкое применение в условиях оптимизации организации и обработки больших объемов данных. Техноло-гии распределения данных уже около 2 десятилетий и развила главные идеи поддержки взаимодействия распределенных и запрашиваемых данных. Но и в настоящий момент, в связи с распространением мультимедиа и гипермедиа информации, которые обладают большими размерами и / или свойством распределенности, проблема распределенных данных не утрачивает своей актуальности.

В РБД запросы требуют доступа к данным от одного или нескольких узлов. Затраты на выполнение запроса зависят от расположения запроса так же, как и от расположения данных. То есть расположение данных запроса определяет количество данных, принятых для обработки запроса; улучшение расположения данных уменьшает затраты на передачу данных. Поэтому все сталкиваются с проблемой размещения данных, цель которой – улучшить расположение данных. Представлен набор запросов, обращающихся к набору фрагментов данных, алгоритм распределения данных распределяет эти фрагменты по узлам РБД с целью минимизации общих затрат на передачу данных для обработки запросов. В РБД фрагмент данных соответствует отношению или горизон-тальному/вертикальному фрагменту отношения, объект мультимедийных данных подобно звуковому файлу или видеоклип, или гипермедиа-документ подобно веб-странице. Отсюда, используя генетическое отношение фрагментов, формулируется проблема размещения данных, и разрабатываются алго-ритмы, которые могут разрешить проблему для специализированных приложений, объединяя зависимость между обработкой запроса и размещением данных.

Оптимальное распределение фрагментов является темнее менее комплексом проблем так как существует взаимная зависимость между схемой распределения (которая показывает расположение каждого фрагмента на различных узлах базы данных) и стратегией оптимизации запросов (которая решает как может быть оптимально выполнен на схеме размещения). Граф зависимости фрагментов моделирует отношения между фрагментами и количество передаваемых данных, нужных чтобы выполнить запрос. Граф зави-симости фрагментов, расположенный на рис. 1, представляет собой направленный ациклический граф, вершиной которого является сайт генерации запроса (сайт Q) а все другие узлы как узлы фрагмента (сайт G, например) на потенциальных сайтах доступных запросу. Направленное ребро между двумя сайтами показывает количество передаваемых данных, если фрагменты в этих узлах расположены на различных сайтах. Количество передаваемых данных (например, size (G’’)) зависит от обрабатываемого запроса и может быть меньше чем размер доступного фрагмента (то есть size(G’’)


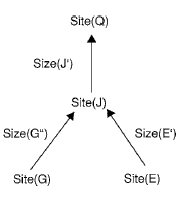
Рисунок 1. Граф зависимости фрагментов (ГРФ)

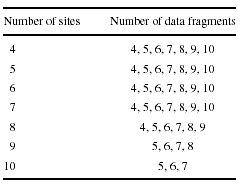
Алгоритм распределения данных имеет следующие входные параметры: (I) Граф зависимости фрагментов; (II) Затраты на передачу данных между сайтами; (III) Ограничение на размещение количества фрагментов на сайтах; and (IV) Частота выполнения запросов от сайтов. Задача этой работы - разработать быстрые и эффективные алгоритмы, которые могут генерировать схемы размещения с минимальной стоимостью передачи. Мы рассматривает только безубыточное размещение данных (т.е., каждый фрагмент размещается точно в одном узле).

Рассмотрим базу данных, состоящую из 4 узлов и двух типов запросов, приведенную на рисунке 2. Стоимость передачи данных и граф зависимости запросов приведены на рисунке 2. Требуется распределить 4 фрагмента данных на четырех взаимосвязанных узлах чтобы затраты на передачу данных для двух запросов были минимальными. Каждый запрос имеет различную частоту доступа на каждый сайт; то есть, на каких-то сайты запрос может быть вызван гораздо чаще, чем на других. Таким образом, общий объем данных, требуемый для выполнения запросов, может значительно отличаться для различных моделей распределения данных. Как будет показано впоследствии, поиск лучшей модели размещения данных - это комплексная проблема даже для маленьких примеров. Действи-тельно, проблема размещения данных в системе РБД известна, как NP-полная [9, 11, 12, 19], и поэтому, оптимальные решения не могут быть найдены в рациональные сроки даже для умеренного размера задачи. Задача этой работы - ввести эволюционный и основанный на эвристическом поиск для решения проблемы размещения данных, стремящийся получить решения высокого качества в достаточно быстрые сроки.


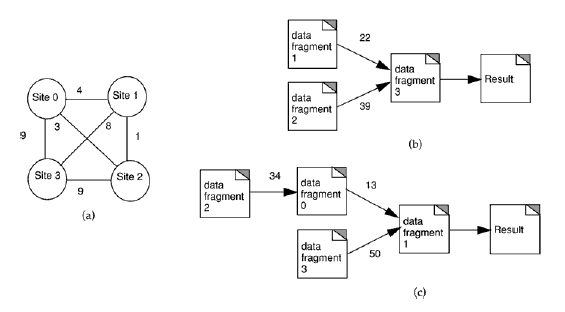
Рисунок 2. – Распределенная база данных и граф зависимости фрагментов.а) Сеть распределенной базы данных; б) Граф зависимости фрагментов для запроса 1-го типа; в) Граф зависимости фрагментов для запроса 2-го типа

2. Существующие работы

Проблема размещения данных изучена в контексте размещения файлов в распределенной вычислительной системе. Проблема размещения файлов, однако, не принимает во внимание семантику обработки файлов, тогда как проблема размещения данных должна принять во внимание взаимосвязь среди доступов к составным фрагментам запросов. Chu [9] изучал проблему размещения записей файла относительно составных файлов на мультипро-цессорной системе, и представлял модель глобальной оптимизации, чтобы минимизировать полные затраты обработки по вынужденному времени отве-та и емкости запоминающего устройства с фиксированным числом копий каждого файла. Casey [6] делал различия между обновлениями и запросами к файлам. Eswaran [11] доказал, что формулировка Casey является NP-полной, и предложил эффективную эвристику.

Ramamoorthy и Wah [28] проанализировали проблему размещения записей файла в среде распределенной базы данных и разработали приближенный алгоритм для простой проблемы размещения записей файла и обобщенной проблемы размещения записей файла. Ceri и другие [7] рассматривали про-блему размещения записей файла для типичных приложений распределенной базы данных с простой моделью для выполнения транзакций, принимающего во внимание зависимость между доступами к составным фрагментам. Frieder и Siegelmann [12] недавно предложили доказательство, что проблема размещения мультипроцессорного документа (MDAP) NP-полная. В их формули-ровке MDAP, они предполагают, что сущесвует есть целый ряд четких документов, которые собраны в несколько кластеров, чтобы быть распределен-ным целый ряд однородных процессоров. Проблема MDAP уменьшена к би-нарной Quadratic Assignment Problem (NP-полная задача [13]) в полиномиальном времени. Frieder и Siegelmann предложили простой генетический ал-горитм, чтобы разрешить проблему эвристически. Следует отметить, что проблема MDAP не рассматривает структур запроса доступа к документам; тогда как в настоящей работе, запросы моделируются, так как направленные графы переноса данных, которые играют жизненно важную роль в рассмат-риваемой проблеме размещения данных.

Apers [1] рассматривал размещение распределенной базы данных по уз-лам, чтобы минимизировать полную стоимость передачи данных, и изобрел усложненный подход, путем первичного разбиения отношения на бесконеч-ное число фрагментов, а затем размещение их. Apers объединил системно за-висимую стратегию обработки запроса, с логической моделью для размещения фрагментов. Но помеха - то, что проблема фагментации и размещения исследуются вместе. То есть, схема фрагментации должна быть одним из выходов алгоритма размещения. Это сократит применимость этой методологии, когда схема фрагментации уже определена и должнабыть определена схема размещения.

Cornell и Yu [10] предложил стратегию, чтобы объединить определение назначения отношения и стратегию запросов, чтобы оптимизировать работу системы распределенной базы данных. Даже если они приняли во внимание стратегию выполнения запроса, их решение линейного программирования достаточно сложное. Другая проблема в их подходе - это отсутствие упроще-ния как в объединении стратегии выполнения запроса, так и процедуре ре-шения. Несколько других формулировок линейного программирования также предложены для проблемы размещения данных [14, 27]. Главная проблема в этих подходах - это отсутствие моделирования стратегии выполнения запроса. Lin и [15] другие разработал эвристический алгоритм для минимальной стоимости передачи данных, рассматривая репликацию фрагментов как для операции чтения, так и обновления.

В дальнейшем, мы представляем исчерпывающее изучение эволюционных алгоритмов размещения данных, сосредоточивающиеся на качестве решения, времени и пространственной сложность. В частности, мы предложили четыре различных алгоритма, каждый основанный на различных эвристиках, и оцениваем их результаты, сравнивая исчерпывающие решения.

3. Проблема размещения данных

В этом разделе, мы обсудим подробно проблему размещения данных и характеризуем лежащую в основе распределенную систему мультимедийной базы данных. В таблице 1 приведены условные обозначения.

Рассмотрим распределенную базу данных, состоящую из m sites, узлов, каждый из узлов имеет свою производительность, объем памяти, и локальную базу данных. Узлы Si. m узлов в РБД объединены в сеть. Соединение между двумя сайтами Si И Si' (if it exists) характеризуется целочисленной положительной переменной cii' которая ассоциируется с затратами на передачу данных от узла Si к узлу Si'. Если два узла не соединены напрямую, затраты на передачу данных состоят из суммы затрат передачи данных через выбранный путь. Пусть Q ={q0, q1, . . . , qn-1} наиболее часто применяемые запросы, которые составляют более чем 80% функционирования базы данных. Каждый запрос qx может быть выполнен с каждого узла с определенной частотой. Пусть aix частота, с которой запрос qx is выполняется на узле Si. Частота выполнения n запросов с m сайтов может быть представлена с помощью матрицы А размером m*n. Пусть будет k daфрагментов данных {O0, O1, . . . , Ok-1}.

Table 1. Условные обозначения


3.1. Представление запросов

Проблем размещения данных является сложной из-за сложной взаимоза-висимости между стратегией выполнения запросов (зависящей от оптимиза-тора запросов) и расположения фрагментов. Оптимальное расположение фрагментов зависит от данной стратегии выполнения запросов и стратегия выполнения запросов зависит от расположения фрагментов (т.е. фрагментов, доступных запросу). Главная проблема в решении оптимального расположе-ния – недостатки моделей, которые представляют зависимости между фраг-ментами, доступными запросу. Эти зависимости возникают из-за разделения отношения на фрагменты и/или доступа запросами к множественным отношениям. Используется декомпозитор распределенных запросов и алгоритм раз-мещения данных [22] для разделения распределенного запроса на множество фрагментов запроса. Этот декомпозированный запрос соединяет зависимости между фрагментами. Эта зависимость моделирует бинарные операции (например, join, union) между фрагментами, которые нужно обработать в соответствии с выполняемым распределенными запросом. Мы оцениваем разме-ры промежуточных отношений, генерируемых после выполнения унарных и бинарных операций, используя статистику базы данных (например, мощ-ность и длина кортежей фрагментов) доступную из системного каталога. С тех пор, как мы объединяем распределенную обработку запроса, фазы де-композиция запроса и размещения данных исключают доступ к ненужным фрагментам и генерируем сжатый оператор декомпозированного запроса, разбитый на фрагменты. В оптимизации распределенных запросов и фазе выполнения оптимальные бинарные операции выбираются на основе стратегии выполнения запросов:

  1. Move-Small: Если в бинарной операции участвуют два фрагмента, расположенные на двух разных узлах, тогда отправляется меньший по размеру фрагмент на узел с большим фрагментом.

  2. Query-Site: Отправляются все фрагменты на узел, на котором вызван запрос и выполняется этот запрос.


Отметим, что задачей размещения данных является минимизировать общие затраты на передачу данных для обработки всех запросов используя одну из стратегий выполнения запросов. Первой целью размещения данных является оптимизировать расположение фрагментов для выполнения запро-сов. Второй является объединить стратегию выполнения запросов когда запрос требует обращения к фрагментам от составных узлов и сократить затра-ты на передачу данных при выполнении всех запросов.

3.2. Модель затрат на передачу данных

Существует два вида стоимости передачи данных. Первый тип затрат существует благодаря перемещению данных узла размещения данных на узел, где запрос инициирован. Второй тип затрат заключается когда данные с сайта где расположен один из фрагментов передаются туда, где расположен второй фрагмент. В первом случае размер фрагмента данных, требуемых в каждого сайта не изменяется с расположением фрагментов данных и нет зависимости меж-ду фрагментами данных, доступных запросу. Это справедливо в случае стратегии выполнения запросов Query-Site.

Пусть rxj будет определено как размер фрагмента данных Oj которые нужно передать на узел, где запрос qx инициирован. Матрица передачи R размером n*k. Это объединяет верхний уровень графов зависимости данных. Пусть будет запрос qx инициированный на сайте Si, aix раз за опредеелнный временной интервал. Пусть U матрица m*k матрица где uij – количество данных, которые нужно передать с узла, где расположен фрагмент данных Oj на узел Si где запрос был инициирован. Тогда,

И в матричном представлении,U = A*R

Второй тип стоимости передачи данных соответствует более глубоким уровням графов зависимости данных. Данные передаются с узла где распо-ложен один фрагмент в порядке выполнения бинарных операций, вовлекаю-щих два или более фрагментов данных. В данном случае количество данных фрагмента требуемый с каждого сайта, зависит от расположения остальных фрагментов данных. Пусть djj' определяется размер данных из фрагмента Oj который нужно передать на узел, где Oj' расположен, чтобы выполнить определенную бинарную операцию. Матрица передачи D размером k*k. Это зависит от запроса, который должен быть обработан. То есть для каждого запроса мы должны знать, информацию о том, какое количество данных нужно передать от узла, где расположен один фрагмент, на узел, где другой фрагмент данных расположен, при этом оба фрагмента данных должны быть доступны для выполнения запроса. Эта информация извлечена генератором графа зависимости фрагментов данных, который обрабатывает деревья оператора запроса на фрагменты, обращая стратегию выполнения запроса и представлена в виде графа зависимости фрагментов данных.

Пусть dxjj' размер данных узла Oj которые нужно передать на узел Oj' для выполнения запроса qx. Получим матрицу Dx . . Количество данных, которые нужно передать с узла Oj на узел Oj' равно:


В матричном представлении,


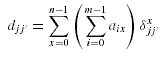
Пусть site(Oj) это узел где фрагмент данных Oj расположен. Тогда, общие затраты на передачу t, равны:


где первое слагаемое означает стоимость передачи данных, принятая чтобы обработать бинарные операции между фрагментами данных располо-женными на различных узлах, а второе слагаемое представляет собой затраты на передачу данных чтобы передать результаты бинарных операций фрагментов данных на узел, где запрос был инициирован. Задача распределения данных состоит в минимизации t изменяя значение site(Oj) (которая проецирует фрагмент данных на сайт).

Для иллюстрации рассмотрим описанный выше пример, где нужно разместить 4 фрагмента данных между 4 узлами. Частоты доступа запроса 0 и 1 на узлы представлены в матрице:


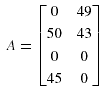
Общая частота доступа запроса равна 95 и 92 соответственно, и матрица затрат зависимости фрагментов данных равна:

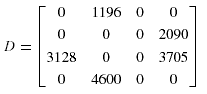
Матрица передачи данных запросов:

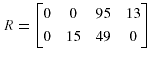
Итак, матрица затрат распределения данных равна:

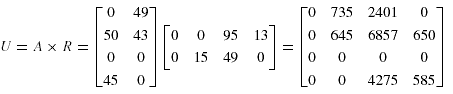
4. Предлагаемые алгоритмы размещения данных

Проблема размещения данных NP-полная вообще и поэтому требует эвристических методов, быстрых и способных к получению высококачествен-ного решения. Разработка эффективной эвристики чрезвычайно зависит от стратегии выполнения запроса, используемой системой распределенной базы данных, так как различные стратегии выполнения запроса имеют различные шаблоны миграции фрагмента данных. Мы развиваем решения для проблемы размещения данных, когда СУРБД и мультимедийный источник данных ис-пользуют соответственно query-site и move-small стратегии выполнения запроса.

Мы предлагаем четыре эвристичкеских поисковых методах, которые показали значительный потенциал в решении широкого ряда других проблем оптимизации [24, 30]. Первый алгоритм основан на традиционном генетическом алгоритме. Второй алгоритм основан на алгоритме симуляции эволю-ции, которая, в противоположность традиционным генетическим алгоритмам, зависит от кроссовера и кодирует информацию в области решения. К тому же, симулирующий алгоритм эволюции использует мутацию в качестве первоначального поискового механизма и кодируют информацию в области решения. Третий алгоритм основан на технике, которая является комбинаци-ей нейронных сетей и симулирует нормализацию. Четвертый алгоритм основан на технике случайного поиска. Эти алгоритмы описаны ниже.


4.1. Генетические алгоритмы

Генетические алгоритмы (ГА) - поисковые методы [16, 17, 21, 30] вдохновлены механизмами естественного генетического лидерства к выживанию соответствующих индивидуумов. Генетические алгоритмы манипулируют популяцией потенциальных решений проблемы оптимизации [30]. Конкрет-но, они оперируют закодированными представлениями решений, эквивалентно генетическому материалу индивидуумов в природе, и не непосредст-венно на решениях непосредственно. В самой простой форме, решения в по-пуляции кодируются как двоичные хромосомы. Как в природе, механизм выбора обеспечивает необходимую движущую силу для лучших решений выжить. Каждое решение связано со значением фитнесс-функции, которое отображает, насколько хорошо оно по сравнению с другими решениями в популяции. Более высокий значение фитнесс-функции индивидуума - более высокий шанс выживания в последующем поколении. Рекомбинация гене-тического материала в генетических алгоритмах симулирует через механизм кроссовера, который обменивает части между хромосомами. Другой опера-тор - мутация, вызывает единичное и случайное изменение отрезков хромосомы. Мутация также имеет прямую аналогию с природой и играет роль возрождения утраченного генетического материала.

В предлагаемом генетическом алгоритме колируются размещение каж-дого фрагмента в двоичном представлении. Если фрагмент данных располо-жен на сайте 3, он представляется значением 11. Представление размещения всех фрагментов данных объединяется в форму двоичной строки. Каждая двоичная строка представляет потенциальное решение задачи размещения данных. Фитнес-функцией строки являются просто затраты на размещение. Механизм выбора происходит по простой пропорциональной схеме выбора: строка с фитнес-функцией f размещает f /(f') потомков, где является средним значением Фитнес-функции для всей популяции.

Кроссовер и другие операторы ГА. Пары строк выбираются в случайном порядке из популяции чтобы быть субъектами кроссовера. Используется простой единичный кроссовер. Предположим что L – это длина строки, алго-ритм произвольно выбирает точку кроссовера, которая может принять значе-ния от 1 до L-1. Части двух строк после точки кроссовера меняются чтобы образовать две новых строки. Точка кроссовера может принимать значения от 1 до L-1 с равной вероятностью. Заметим, что кроссовер выполняет только тогда, когда случайно сгенерированное число больше, чем заранее указанная норма pc (также называется вероятностью кроссовера); иначе строки остаются неизмененными.

После кроссовера строки становятся субъектами мутации. Мутация бита – это изменение бита на противоположное значение. Как и параметр pc кон-тролирует вероятностью кроссовера, другой параметр pm (вероятность мута-ции) задает вероятность с которой бит будет изменен. Биты строки мутируют независимо – т.е. мутация одного бита не влияет на вероятность мутации другого бита. Мутация рассматривается как вторичный оператор с целью восстановления утраченного генетического материала.

Ниже рассмотрен ГА для решения проблемы распределения данных:
(1) Инициализация популяции. Каждый член популяции – конкатенация двоичных представлений н6ачального случайного распределения каждого фрагмента данных.
(2) Оценка популяции.
(3) no-of-generation = 0.
(4) WHILE no-of-generation < MAX-GENERATION DO.
(5)       Выбор хромосом для следующей популяции
(6)       Выполнение кроссовера и мутации для выбранных хромосом
(7)       Оценка популяции
(8)       no-of-generation ++;
(9) ENDWHILE
(10) Определение окончательного размещения, выбирая подходящие хромосомы. Если окончательное размещение недопустимо, то рассматриваем каждый выше-размещенный узел и перемещают фрагменты чтобы возрастание стоимости было минимальным.

Временная сложность ГА размещения данных равна O(GNp(k2 + km)), где G это число поколений и Np это размер популяции.

Для маленькой проблемы размещения показанный раньше в рисунке 2, начальная хромосома GA изображается в рисунке 3(a). После выполнения повтореий генетических операторов, окончательное решение представлено хромосомой, показанной в рисунке 3(b), который представляет размещение: фрагмент данных 0 к узлу 2, фрагмент данных 1 к узлу 1, фрагмент данных 2 к узлу 1, и фрагмент данных 3 к узлу 2. Полная стоимость размещения составляет 67,378. Время решения используя рабочую станцию Sun Ultra , составляет 474 секунды.

a)  (10   11   00   01)       b)  (10   01   01   10)
Рисунок 3. – Начальная (а) и конечная (b) хромосомы ГА

4.2. Алгоритм симуляции эволюции

Этот вариант традиционного генетического алгоритма называется алгоритм симуляци эволюции [18, 19]. Генетические алгоритмы и эволюционные стратегии подобны в использовании вероятностного поискового механизма, направленного в сторону уменьшения или увеличения целевой функции. Эти методы имеют высокую вероятность оптимального размещения глобального решения в поисковом отрезке, несмотря на то, что функция стоимости имеет несколько локальных оптимумов. Эволюционные стратегии используют му-тацию в качестве поисковых механизмов и селекцию, чтобы направить поиск в направлении следующих отрезков в области поиска. Генетические алго-ритмы генерируют последовательность популяций, используя механизм селекции, и используют кроссовер и мутацию как поисковые механизмы.

Принципиальное отличие между генетическим алгоритмом и эволюционной стратегией является то, что результат зависит от кроссовера, меха-низма вероятностей, и полезного обмена информации между решениями, чтобы найти лучшее решение, тогда как последний использует мутацию использований как первоначальный поисковый механизм.
Алгоритм симуляции эволюции:
(1) Сконструировать первую хромосому, основанную на данных задачи, и изменять чтобы сгенерировать начальное решение;
(2) Использовать эвристические методы чтобы генерировать решение для каждой хромосомы;
(3) Оценка полученных решений;
(4) no-of-generations = 0;
(5) WHILE no-of-generations < MAX-GENERATION DO
(6)       Выбор хромосом для следующего поколения
(7)       Применение кроссовера и мутации для этого набора хромосом;
(8)       Использовать эвристические методы чтобы генерировать решение для каждой хромосомы;
(9)       Оценка полученных решений;
(10)      no-of-generations = no-of-generations+1;
(11) ENDWHILE
(12) Вывод лучшего найденного решения

Структура хромосом следующая:

где количество генов а – общее ограничение на количество фрагментов, количество генов b – общее количество фрагментов.

Для части а каждый ген – отдельный бит. Значение 1 указывает, что соответствующее место размещения можно использовать для размещения этой хромосомы. Иначе, если бит равен 0, это место не может использоваться. Это сокращает доверительные границы размещения для каждого узла.Для части b каждый ген является целым числом которое представляет приоритет рассматриваемого фрагмента; большее значение означает больший приоритет и наоборот.

Используя матрицы стоимости передачи данных С, частот доступа за-просов и размеры передаваемых данных, можно вычислить матрицу стоимости размещения фрагментов U' = C * U

Каждое значение u'ij, означает стоимость размещения, если фрагмент j будет размещен на узле i>.Для примера размещения, показанного на рисунке 2, U' равно:

В алгоритме симуляции эволюции первая хромосома в начальной популяции конструируется из u'ij которая как было сказано выше, представляет стоимость размещения фрагмента j на узле i.Для каждого фрагмента j мы вычисляем:
Мы предлагаем минимизировать стоимость размещения давая больший приоритет фрагменту с большим значением Xj (большее значение Xj означает что этот фрагмент будет использовать большее время передачи). Поэтому мы просто назначаем Xj как ген для каждой позиции фрагмента в части b первой хромосомы в начальной популяции.

Все гены в части а начальной хромосомы устанавливаем в 1 для первой хромосомы в начальной популяции, так как это предел размещения первоначальной задачи. Для оставшихся хромосом в начальной популяции гены в части а выбираются случайно 0 или 1. Гены в части b - это изменения соответствующих генов первой хромосомы. Заметим, что для генов в части а мы должны проверить новое ограничение размещения чтобы все гены были размещены. Это может быть сделано просто путем подсчета количества 1 в части а и проверкой, что эта сумма является большей или равной общему числу фрагментов k. k.

Эвристика: Для каждой хромосомы, мы ищем решение путем размещения фрагмента j с наивысшим приоритетом на узел i так что u'ij является наименьшим для всех u'xj, 1<x<m. Если предел размещения фрагментов для этого узла превышен (узел уже насыщен), мы размещаем этот фрагмент на узел со следующим наименьшим значением u'ij для всех u'yj, 1&ly&lm, y <>x x. Это гарантирует что фрагмент будет размещен на какой-либо сайт, так как мы проверили что общее ограничение на размещение больше или равен общему числу фрагментов для каждого поколения хромосомы. Далее мы продолжаем процесс для следующего фрагмента с самым высоким приоритетом среди тех, что еще не размещены.

Целевая функция: Для каждой хромосомы целевая функция является общими затратами после размещения всех фрагментов на сайты используя эвристику. Для вычисления этой функции будет рассматривать как зависимость фрагментов, так и размеры фрагмента для каждого узла. Значение ЦФ для хромосомы будет вычислено как:

где Np размер популяции, MaxCost максимальное значение затрат на передачу среди хромосом популяции, и tau параметр сходимости.

Генетические операторы: Два генетических оператора – селекция и кроссовер. Для их иллюстра-ции рассмотрим две хромосомы до операции кроссовера c1 and c2. Предположим что точка кроссовера z, то есть,

c1:c11c12      and      c2:c21c22

где количество генов в c11 и c21 равно z. Эти хромосомы после кроссовера,

c'1:c12c12      and       c'21c22

Для генов а мутация изменяет значение для 1 или 0. Для генов b изменяем значение гена путем добавления случайно выбранного значения от -n до m (n и m являются максимальными значениями генов в этой хромосоме деленных на 4). Мы должны проверять достоверность предела размещения фрагментов в каждой хромосоме (т.е. сумма единиц для генов a>=k, количества фрагментов).

В отличие от предыдущего алгоритма, нам не требуется проверять дос-товерность полученного решения так как мы явно кодируем ограничение на размещение фрагментов в хромосоме и гарантируем, что эти ограничения не будут избыточных для всего полученного решения.

Для примера размещения, показанного на рисунке 2, начальная хромо-сома алгоритма изображена на рисунке 4. Подобно ГА, с итеративным применением кроссовера, мутации и селекции, конечное решение сводится в одну точку: фрагмент данных 0 к узлу 1, фрагмент 1 к узлу 2, фрагмент 2 к узлу 1 и фрагмент 3 к узлу 2. Общие затраты на размещение равны 57,470, что является оптимальным значением. Время решения равно 79 секундам.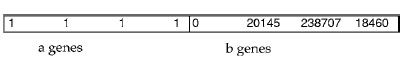


Figure 4. The initial chromosome of the SE algorithm.

4.3. Алгоритм поиска средних величин

Техника MFA [3,5,25] объединяет общие вычисления нейронных сетей с симуляцией [32]. MFA было первоначально предложено для решения задачи коммивояжера как альтернатива HNN, который не работает хорошо для задач большого размера. Показано что MFA это общий подход [3,4] который может быть применен к различным задачам оптимизации. Опишем общую формулировку MFA [3]. Алгоритм выводится по анало-гии с моделью Ising spin которая используется чтобы оценить состояние час-тиц или спинов в тепловом равновесии. В модели Ising spin энергия системы c S спинами имеет следующую форму:

где bxy представляет уровень взаимодействия между спинами х и у, и sx = {1, 0} значение спина х. Предполагается что bxy = bxy и bxx = 0 для 1<=x, y<=S. В тепловом балансе, среднее значение спина <sx> спина х может быть рассчитано используя распределение Больцмана:

где Фx = <sH(s)>|sx=0 - <H(s)>|sx=1 представляет поле усредненных величин действующих на спин х, где средняя энергия системы равна <sH(s)>:

Сложность вычисления Фx используя указанное выше распределение возрастает экспоненциально. Однако, для большого числа спинов поле усредненных величин может использоваться для вычисления средней энергии как:

Отсюда <sH(s)> является линейной относительно <ssx>, поле усредненных величин Фx может быть вычислено используя формулу:
Таким образом, сложность вычисления Фx сокращает O(S).

Для каждой температуры, начинающейся с начальных средних спинов, вычисляется поле средних величин Фx действующих на случайно выбранный спин. Затем средний спин обновляется. Этот процесс повторяется для случайной последовательности спинов пока система не стабилизируется для текущей температуры.

Сформулирует задачу распределения данных для MFA в следующей форме. Вместо массива линейных спинов, матрицу (sij) мы использовали для кодирования размещения фрагментов данных по узлам. Матрица состоит из х строк и m столбцов, представляя х фрагментов данных и m узлов. Значение 1 указывает что фрагмент данных расположен на соответствующем узле. На-пример, если ssij = 1, то фрагмент данных i расположен на узле j. Допустимость размещения проверяется так: в каждой строке должно быть не более 1 единицы. Каждая спиновая переменная – непрерывная величина в интервале от 0 до 1. Значения этой переменной сводят к 1 или 0 в фиксированной точке. Представленная здесь формулировка, функция энергии (т.е. функция стоимо-сти передачи данных) для задачи распределения данных может быть формализована как описано ниже:

Поле усредненных величин Фij равно by spin sij is:

В реальном размещении, каждый фрагмент данных должен быть распо-ложен только на один узел. Поэтому, сумма спинов по каждой строке матри-цы должны быть равна единице. Это ограничение может явно обрабатываться при изменении, нормализуя каждый спин sij Как
Временная сложность для одной итерации равно О(k(k + m)). Используя линейный список с k значениями температуры и принятом ограничении в В итераций, полное время выполнения алгоритма: O(BK(k2 + km)).

4.4. Случайный окрестный поиск

Мы используем низкой сложности, но эффективную технику оптимизации, известную как случайный окрестный поиск [24]. Главная идея алгоритма – генерировать начальное решение с умеренным качеством. Затем, в соответствии с некоторым заранее определенным соседством, алгоритм вероятностно выбираем и проверяет лучшее ли соседнее в области поиска решение или нет. Если новое решение будет лучше, алгоритм принимает это значение и запускает поиск в новом соседстве; иначе, алгоритм выбирает другую точку решения. Алгоритм останавливается после того, как выполнится указан-ное число шагов поиска или решение не улучшается после некоторого числа шагов. Качество решения окрестного поиска сильно зависит от конструкции соседства решения.

Для примера задачи, изображенной на рисунке 2, распределение, сгенерированное данным алгоритмом имеет вид: фрагмент 0 к узлу 1, фрагмент 1 к узлу 2, фрагмент 2 к узлу 2, фрагмент 3 к узлу 2. Затраты на распределение этой задачи равно 65,624. Затраты на время равно 31 секундам. От маленькой задачи размещения с рисунка 2, мы может увидеть, что этот алгоритм генерирует лучшее (оптимальное) решение, но использует среднее время решения. Алгоритм MFA является самым быстрым, но качество решения неудовлетворительно. Подобный аргумент справедлив и для алгоритма случайного поиска. ГА представляется наихудшим, так как качество решения самое плохое, и занимает самое длинное время решения.

5. Результаты эксперимента

Чтобы понять достоинства и недостатки четырех предложенных алгоритмов размещения данных, представим результаты экспериментов. Сравне-ния выполнены относительно качества решения и времени решения. Для сравнения получены оптимальные решения используя полный перебор. Мы применили алгоритмы к ситуациям, показанным в таблице 2.

Для каждой ситуации мы сгенерировали 100 различных примеров задачи со случайной конструкцией графов и случайным выбором количества запросов с нормальным распределением в интервале [10, 20]. Поэтому общее ко-личества примеров задачи равно 4.100. Так как величины фрагментов данных критически влияют на качество окончательного распределения [19], мы выполним алгоритмы с шестью различными значениями величин фрагментов данных. Мы сразу зафиксировали среднюю стоимость передачи данных по сети равной 10 единицам данных в единицу времени (в интервале [1, 20]). Затем м генерировали шесть размеров средних фрагментов данных, умножая среднюю стоимость передачи по сети на шесть стоимостных коэффициентов: 1, 5, 25, 100, 250 и 500. Интервалы также умножаем на коэффициенты. Об-щее количество тестов равно 24.600. Средние отклонения от оптимальных решений для четырех алгоритмов показаны в Таблице 3. Одно непосредственное наблюдение - то, что все ал-горитмы выполняются лучше для больших соотношений затрат. Так как ес-ли размеры фрагмента данных сравнимы со скоростью сети, время ответа становится наиболее чувствительным к размещению фрагментов данных по узлам. С другой стороны, если размеры фрагмента данных намного большие, чем скорость сети, время ответа не будет находится под большим влиянием от размещения, но будет скорее зависеть от зависимости фрагментов данных в графах запроса. Для малых соотношений затрат, алгоритм симуляции эво-люции, выполняется лучше, чем другие три алгоритма. Однако, когда эф-фект соотношения затрат насыщается (в соотношении = 100), ГА работает лучше остальных. MFA был хуже, чем RS для малых соотношений, но вы-полняется лучше для больших соотношений.

Таблица 2. – Вид контрольный тестов

Таблица 3. – Средний % отклонения от оптимума четырех алгоритмов для различных соотношений затрат

6. Выводы

В этой работе, мы обращаемся к проблеме размещения неизбыточных фрагментов данных в системе РБД. Мы разработали управляемый запроса-ми подход к размещению данных, объединяющий стратегию выполнения запроса с формулировкой проблемы размещения данных. Мы также предложи-ли различные алгоритмы, основанные на эволюционной вычислительной парадигме, для решения проблемы размещения данных в системах РБД. Глав-ный вклад этой работы - это разработка независимого от узла графа зависи-мости фрагментов для представления затрат передачи данных, возникающих при выполнении запроса, используя особенную стратегию выполнения за-проса. Это предоставляет возможность приложению с управляемым запро-сами подходом к размещению распределять объекты базы данных по различ-ным системам БД (например, реляционной, объектно-ориентированной, сети, и т.п.) и облегчает разработку обобщенной структуры, в пределах которой определить и разрешить проблемы размещения данных.

В наших обширных экспериментальных изучениях, мы оценили и срав-нили четыре предложенные эвристики размещения данных, в том числе гене-тический алгоритм (GA), симулирующий алгоритм эволюции (SE) , MFA, и алгоритм случайного поиска (RS), в условиях продолжительности ответа на запрос и времени выполнения алгоритма. Интересное результат - то, что ни-какой один алгоритм не является лучше всех остальных в обоих аспектах. SE и GA может генерировать лучшие решения, чем RS и MFA в общем. Тем не менее, разница в качестве решения есть не всегда такой же величины. К то-му же, алгоритм RS имеет самую низкую временную сложность, которая делает это самым быстрым алгоритмом, тогда как SE алгоритм абсолютно мед-ленный. В течение быстрого времени выполнения и малого отклонения от оптимального ренения, алгоритм RS - это жизнеспособный выбор. С другой стороны, когда эффективность и качество решения одинаково важна, GA, возможно, является более привлекательным выбором. Поэтому, преимущест-во наличия этих алгоритмов в РБД - это пригодность разных пределов качества решения и трудности компромисса.

References

  1. P.M.G. Apers, “Data allocation in distributed database systems,” ACM Transactions on Database Systems, vol. 13, no. 3, pp. 263–304, 1988.
  2. P.B. Berra, C.Y.R. Chen, A. Ghafoor, C.C. Lin, T.D.C. Little, and D. Shin, “Architecture for distributed multimedia systems,” Computer Communications, vol. 13, no. 4, pp. 217–231, 1990.
  3. D.E. Van den Bout and T.K. Miller, “Graph partitioning using annealed neural networks,” IEEE Transactions on Neural Networks, vol. 1, no. 2, pp. 192–203, 1990.
  4. D.E. Van den Bout and T.K. Miller, “Improving the performance of the Hopfield-Tank neural network through normalization and annealing,” Bio. Cybernet, vol. 62, pp. 129–139, 1989.
  5. T. Bultan and C. Aykanat, “A new mapping heuristic based on mean field annealing,” Journal of Parallel and Distributed Computing, vol. 16, pp. 292–305, 1992.
  6. R.G. Casey, “Allocation of copies of a file in an information network,” in Proceedings of the Spring Joint Computer Conference, IFIPS, July 1972, pp. 617–625.
  7. S. Ceri, G. Martella, and G. Pelagatti, ‘Optimal file allocation for a distributed on a network of minicomputers,” in Proceedings of the International Conference on Databases, July 1980, pp. 345–357.
  8. S. Ceri and G. Pelagatti, Distributed Databases: Principles and Systems, McGraw Hill: New York, 1984.
  9. W.W. Chu, “Optimal file allocation in a multiple computer system,” IEEE Transactions on Computers, vol. C-18, no. 10, 1969.
  10. D.W. Cornell and P.S. Yu, “Site assignment for relations and join operations in the distributed transaction processing environment,” in Proceedings of the IEEE International Conference on Data Engineering, Feb. 1988.
  11. K.P. Eswaran, “Placement of records in a file and file allocation in a computer network,” Information Processing, 1974, pp. 304–307.
  12. O. Frieder and H.T. Siegelmann, “Multiprocessor document allocation: A genetic algorithm approach,” IEEE Transactions on Knowledge and Data Engineering, vol. 9, no. 4, pp. 640–642, 1997.
  13. M.R. Garey and D.S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness, Freeman: New York, 1979.
  14. B.Gavish and H. Pirkul, “Computer and database location in distributed computer systems,” IEEETransactions on Computers, vol. C-35, no. 7, pp. 583–590, 1986.
  15. A. Ghafoor, “Multimedia database management systems,” ACMComputing Surveys, vol. 27, no. 4, pp. 593– 598, 1995.
  16. D.E. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning, Addison-Wesley: Reading, MA, 1989.
  17. S. Hurley, “Taskgraph mapping using a genetic algorithm: A comparison of fitness functions,” Parallel Computing, vol. 19, pp. 1313–1317, 1993.
  18. K. Karlapalem and M.-P. Ng, “Query-driven data allocation for distributed database systems,” in Proceedings of 8th International Conference on Database and Expert Systems Applications, Sept. 1997, pp. 347– 356.
  19. Y.-K. Kwok, K. Karlapalem, I. Ahmad, and M.-P. Ng, “Design and evaluation of data allocation algorithms for distributed multimedia database systems,” IEEE Journal on Selected Areas in Communications, vol 14, no. 7, pp 1332–1348, 1996.
  20. T.D.C. Little and A. Ghafoor, “Synchronization and storage models for multimedia objects,” IEEE Journal on Selected Areas in Communications, vol. 8, no. 3, pp. 413–427, 1990.
  21. S.W. Mahfoud and D.E. Goldberg, “Parallel recombinative simulated annealing:Agenetic algorithm,” Parallel Computing, vol. 21, pp. 1–28, 1995.
  22. T. Ozsu and P. Valduriez, Principles of Database Systems, Prentice-Hall: Englewood Cliff, NJ, 1991.
  23. M.T. Ozsu, D. Szafron, G. El-Medani, and C. Vittal, “An object-oriented multimedia database system for a news-on-demand application,” Multimedia Systems, vol. 3, no. 5/6, 1995.
  24. C.H. Papadimitriou and K. Steiglitz, Combinatorial Optimization: Algorithms and Complexity, Prentice-Hall: Englewood Cliffs, NJ, 1982.
  25. C. Peterson and B. Soderberg, “A new method for mapping optimization problems onto neural networks,” International Journal of Neural Systems, vol. 1, no. 3, 1989.
  26. T.C. Rakow, E.J. Neuhold, and M. Lohr, “Multimedia database systems: The notions and the issues,” in Tagungsband GI-Fachtagung Datenbanksystems, Buro, Technik and Wissenschaft (BTW), Dresden Marz 1995, Springer Informatik Aktuell, Berlin, 1995.
  27. S. Ram and R.E. Marsten, “A model for database allocation incorporating a concurrency control mechanism,” IEEE Transactions on Knowledge and Data Engineering, vol. 3, no. 3, pp. 389–395, 1991.
  28. C.V. Ramamoorthy and B.Wah, “The placement of relations on a distributed relational database,” in Proceedings of the 1st International Conference on Distributed Computing Systems, Oct. 1979, pp. 642–649.
  29. P.I. Rivera-Vega, R. Varadarjan, and S.B. Navathe, “Scheduling data redistribution in distributed databases,” in Proceedings of the IEEE International Conference on Data Engineering, Feb. 1990.
  30. M. Srinivas and L.M. Patnaik, “Genetic algorithms: A survey,” Computer, vol. 27, no. 6, pp. 17–26, 1994.
  31. B.Wilson and S.B. Navathe, “An analytical framework for the redesign of distributed databases,” in Proceedings of the 6th Advanced Database Symposium, 1986.
  32. L. Yong, K. Lishan, and D.J. Evans, “The annealing evolution algorithm as function optimizer,” Parallel Computing, vol. 21, pp. 389–400, 1995.

      33.