Source: Rafael C.Gonzalez, Richard E.Woods "Digital image processing"

Перевод выполнен Гетт А.М.

5.3.1 Средние Фильтры

В этой секции, которую мы обсуждаем кратко,рассмотрим шуморедукционные пространственные фильтры введенны в разделе 3.6 и несколько других фильтров.

Фильтр среднего арифметического

Это простейший средний фильтр. Допустим, Sxv представляет набор координат прямоугольной области изображения размером m X n, с центром в точке (x, y).Среднее арифметическое, фильтрующее процесс, вычисляет среднюю величину зашумленного образа g(x, y) в области определенной Sxy.Величина восстановленного образа в любой точке (x, y), - просто среднее арифметическое вычисленное, используя пиксели в области определенном S. Другими словами:

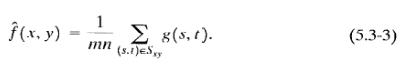
Это действие может быть осуществлено используя маску свертки в которой коэффициенты имеют величину 1/mn. Как обсуждено в Разделе 3.6.1, просто средние плавные локальные изменения фильтра в образе. В результате шум уменьшен.

Геометрический средний фильтр

Образ восстановленный, используя геометрический средний фильтр использует выражение

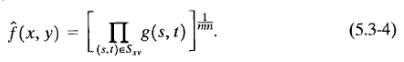
Здесь, каждый восстановленный пиксель выражен пикселей в части изображения окна, поднят в мощность 1/mn. Как показано в примере 52, геометрический средний фильтр достигает шумоподавления в сравнении с фильтром среднего арифметического с меньшей потерей деталей образа в процессе.

Гармонический средний фильтр

Гармонический фильтр опиывается выражением

Гармонический средний фильтр хорошо подавляет соленый шум, но терпит неудачу для шума перца. Этот фильтр преуспевает также с другими типами шума, такими как шум Гаусса.

Контрогармонический средний фильтр

Контрогармонический фильтр опиывается выражением

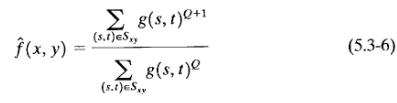
где Q показывает порядок фильтра. Этот фильтр хорошо подходит для уменьшения или фактически устраняет эффекты соли - и - перца. Для положительных величин Q, фильтр устраняет шум перца. Для отрицательных величин Q, он устраняет соленый шум. Это нельзя делать одновременно. Отметим, что Контрогармонический фильтр сводится к фильтру среднего арифметического если Q = 0, и к гармоническому среднему фильтру если Q = - 1

5.3.2 Фильтры порядка и статистики

Фильтры порядка и статистики были введены в Раздел 3.6.2. Мы теперь расширяем дискуссию в этой секции и вводим немного дополнительных фильтров порядка и статистики. Как отмечено в Разделе 3.6.2, Фильтры порядка и статистики являются пространственными фильтрами, чей ответ основан на упорядочении (ранжирование) пикселов содержащихся в области образа. Ответ фильтра в любой точке определен ранжированием результата.

Самый известный фильтра - фильтр медианы, который, как и подразумевает имя, заменяет величину пикселя медианой серых уровней в районе этого пикселя:

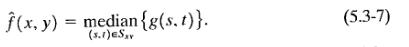
Оригинальная величина пикселя включена в вычисление медианы. Медианный фильтр очень популярен поскольку, подавляет шума произвольного типа, он обеспечивает отличные шуморедукционные возможности. Фильтр Медианы - особенно эффективен в присутствии как биполярного так и униполярного импульса шума . Фактически, как показано в примере 5.3, фильтр медианы дает отличные результаты для образов искаженных этим типом шума. Вычисление медианы и реализации этого фильтра обсуждаются подробно в Разделе 3.6.2.

Фильтр макимума и минимума

Хотя фильтр медианы является очень популярным,но никоим образом не единственным. Медиана представляет 50-ти процентное упорядочевание чисел, но ранжирование годится для много других возможностей. Например, используя 100-й процентные результаты в так называемом фильтре максимума:

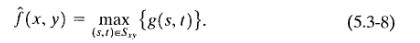
Этот фильтр полезный для обнаружения ярких точек в образе. Также, поскольку шум перца имеет очень низкие величины, он уменьшен этим фильтром в результате процесса максимизации выбора в части изображения области S., 0-й процентный фильтр является фильтром минимума.