Открываем Excel (в нашем случае это Excel 2000). Вносим исходные данные (Табл. №№1-3) в таб-лицу Excel. В результате получаем таблицу, приведенную на рис. 1. Сохраним таблицу. Для этого выбираем в меню Файл, выбираем Сохранить как, выбираем нужную папку, присваиваем имя таблице (в нашем случае Шихта1) и нажимаем Сохранить.
Рисунок 1
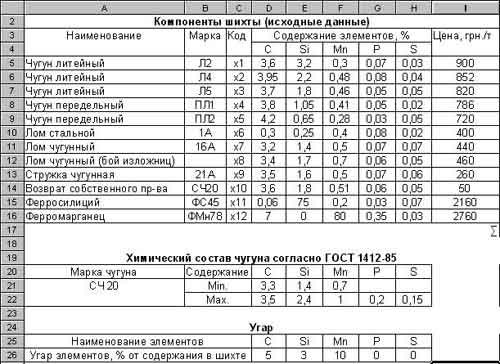
Предварительные расчеты
Для
окончательного формирования банка исходных данных необходимо определить
химический состав чугуна с учетом угара элементов. Для этого в ячейках
J19; O22 построим таблицу 4.
|
Табл. 4. |
J |
K |
L |
M |
N |
O |
|
19 |
Требуемый химический состав чугуна с
учетом угара, % |
|||||
|
20 |
Элементы |
C |
Si |
Mn |
P |
S |
|
21 |
Min. |
C |
Si |
Mn |
P |
S |
|
22 |
Max |
C |
Si |
Mn |
P |
S |
Выделяем
маркером ячейку К21 и вводим в нее следующее выражение
=D21*0,01*(100+D26), нажи-маем Enter, т.е. минимально-допустимое
содержание углерода в чугуне по ГОСТ1412-85 (ячейка D21) уве-личено на
процент угара углерода (ячейка D26).
По данной схеме вводим выражения в
оставшиеся ячейки таблицы:
|
Адрес ячейки |
Выражение |
|
K22 |
=D22*0,01*(100+D26) |
|
L21 |
=E21*0,01*(100+E26) |
|
L22 |
=E22*0,01*(100+E26) |
|
M21 |
=F21*0,01*(100+F26) |
|
M22 |
=F22*0,01*(100+F26) |
|
N22 |
=G22*0,01*(100+G26) |
|
O22 |
=H22*0,01*(100+H26) |
В результате мы получили таблицу (см. рис. 2) в, которой в автоматическом режиме будет отражаться химический состав чугуна с учетом угара.
Рисунок 2

Часть 2. ОПТИМИЗАЦИЯ
Теоретическая справка
В разнообразных экономических моделях планирования производства в качестве оптимального принимается план, обеспечивающий заданный производственный результат при минимальных затратах. Решением подобных задач занимается математическое программирование, наиболее изученным разделом которого является линейное программирование. В нашем случае будет использован получивший наибольшее распространение - симплекс метод, предложенный Дж. Данцигом, с помощью которого можно решить любую задачу линейного программирования.
Постановка задачи
Математически задача оптимизации состава шихты состоит в поиске минимального значения линейной функции (1):

где X1, X2, …, Xn - содержание компонентов в шихте, %;
С1, С2, …, Сn - цена компонентов шихты, грн./т.
В нашем конкретном случае функция (1) приобретает вид:
Z=900X1+852X2+820X3+786X4+720X5+400X6+440
|
Адрес ячейки |
Выражение |
|
L5 |
=J5*L17 |
|
L6 |
=J6*L17 |
|
L7 |
=J7*L17 |
|
L8 |
=J8*L17 |
|
L9 |
=J9*L17 |
|
L10 |
=J10*L17 |
|
L11 |
=J11*L17 |
|
L12 |
=J12*L17 |
|
L13 |
=J13*L17 |
|
L14 |
=J14*L17 |
|
L15 |
=J15*L17 |
|
L16 |
=J16*L17 |
X7+460X8+260X9+50X10+2160X11+ 2760X12 --> Min;
при наличии линейных ограничений, заданных системой равенств и неравенств (3) - (24):
Ограничения по химическому составу:
· Содержание углерода
3,6Х1+3,95Х2+3,7Х3+3,8Х4+4,2Х5+0,3Х6+3,2Х7+3,4Х8+3,5Х9+3,6Х10+0,06Х11+7Х12>=3,465 (3)
3,6Х1+3,95Х2+3,7Х3+3,8Х4+4,2Х5+0,3Х6+3,2Х7+3,4Х8+3,5Х9+3,6Х10+0,06Х11+7Х12<=3,675 (4)
где 3,465 и 3,675, соответственно, минимально и максимально допустимое содержание углерода в чугуне, с учетом угара.
· Содержание кремния
3,2Х1+2,2Х2+1,8Х3+1,05Х4+0,65Х5+0,25Х6+1,4Х7+1,7Х8+1,6Х9+1,8Х10+75Х11>=1,442 (5)
3,2Х1+2,2Х2+1,8Х3+1,05Х4+0,65Х5+0,25Х6+1,4Х7+1,7Х8+1,6Х9+1,8Х10+75Х11<=2,472 (6)
где 1,442 и 2,472, соответственно, минимально и максимально допустимое содержание кремния в чугуне, с учетом угара.
· Содержание марганца
0,3Х1+0,48Х2+0,46Х3+0,41Х4+0,28Х5+0,4Х6+0,5Х7+0,7Х8+0,5Х9+0,51Х10+0,2Х11+80Х12>=0,77 (7)
0,3Х1+0,48Х2+0,46Х3+0,41Х4+0,28Х5+0,4Х6+0,5Х7+0,7Х8+0,5Х9+0,51Х10+0,2Х11+80Х12<=1,10 (8)
где 0,77 и 1,10, соответственно, минимально и максимально допустимое содержание марганца в чугуне, с учетом угара.
· Содержание фосфора
0,07Х1+0,08Х2+0,05Х3+0,05Х4+0,03Х5+0,08Х6+0,07Х7+0,06Х8+0,07Х9+0,06Х10+0,03Х11+ 0,35Х12<=0,2 (9)
где 0,2 - максимально допустимое содержание фосфора в чугуне, с учетом угара.
· Содержание серы
0,03Х1+0,04Х2+0,05Х3+0,02Х4+0,05Х5+0,02Х6+0,07Х7+0,05Х8+0,06Х9+0,05Х10+0,07Х11+ 0,03Х12<=0,15 (10)
где 0,2 - максимально допустимое содержание серы в чугуне, с учетом угара.
Ограничения на содержание компонентов шихты:
· Сумма компонентов шихты должна составлять 100% или 1 (в относительных единицах)
Х1+Х2+Х3+Х4+Х5+Х6+Х7+Х8+Х9+Х10+Х11+Х12=1 (11)
· Количество образующегося возврата у нас составляет 34%, который мы хотим использовать в пол-ном объеме, следовательно
Х10=0,34 (12)
· Технологические ограничения на использование стружки - до 8%, следовательно
Х9>=0 (13)
Х9<=0,08 (14)
· Считаем, что технологических ограничений по содержанию остальных компонентов шихты не суще-ствует. В этом случае необходимо учесть то, что содержание любого компонента в шихте не может принимать отрицательное значение. Для этого вводим следующие ограничения:
Х1>=0 (15)
Х2>=0 (16)
Х3>=0 (17)
Х4>=0 (18)
Х5>=0 (19)
Х6>=0 (20)
Х7>=0 (21)
Х8>=0 (22)
Х11>=0 (23)
Х12>=0 (24)
Таким образом, решение сформулированной задачи оптимизации сводится к решению задачи целочисленного линейного программирования, а именно к определению таких значений X1, X2, …, X12, удов-летворяющих систему ограничений (3) - (24), при которых целевая функция (2) достигает минимума.
Формирование таблиц результатов оптимизации
Продемонстрируем, как легко реализуется решение такого рода задач в среде электронных таблиц Excel.
Формируем таблицы Результаты оптимизации (ячейки J2 - N17) и Ожидаемый химический состав (ячейки J24 - O26)
В диапазон ячеек J5:J16 вводим произвольные начальные значения переменных Х1, Х2, … Х12; например, нулевое значение - 0. После проведения расчетов в данном диапазоне ячеек будет представлено требуемое содержание каждого компонента шихты в относительных единицах.
В диапазоне ячеек К5:К16 будет представлено содержание каждого компонента шихты в %. Для этого вводим расчетные формулы в каждую ячейку диапазона в соответствии с табл. 5.
Таблица 5
|
Адрес ячейки |
Выражение |
|
K5 |
=J5*100 |
|
K6 |
=J6*100 |
|
K7 |
=J7*100 |
|
K8 |
=J8*100 |
|
K9 |
=J9*100 |
|
K10 |
=J10*100 |
|
K11 |
=J11*100 |
|
K12 |
=J12*100 |
|
K13 |
=J13*100 |
|
K14 |
=J14*100 |
|
K15 |
=J15*100 |
|
K16 |
=J16*100 |
В ячейку К17 введем формулу =СУММ(К5:К16), которая будет осуществлять проверку на суммарное содержание компонентов шихты - 100%.
В ячейку L17 вводим объем завалки, в кг. Мы собираемся плавить 6 т, следовательно, вводим - 6000. В диапазоне ячеек L5:L16 будет представлено необходимое содержание каждого компонента шихты в кг на объем завалки 6 т. Для выполнения расчетов введем формулы в соответствии с табл. 6.
Таблица 6
|
Адрес ячейки |
Выражение |
|
L5 |
=J5*L17 |
|
L6 |
=J6*L17 |
|
L7 |
=J7*L17 |
|
L8 |
=J8*L17 |
|
L9 |
=J9*L17 |
|
L10 |
=J10*L17 |
|
L11 |
=J11*L17 |
|
L12 |
=J12*L17 |
|
L13 |
=J13*L17 |
|
L14 |
=J14*L17 |
|
L15 |
=J15*L17 |
|
L16 |
=J16*L17 |
Удельные затраты на закупку каждого компонента шихты из расчета на 1 т литья будут представлены в диапазоне ячеек М5:М16, а суммарные удельные затраты - в ячейке М17. Для их отображения введем расчетные формулы в соответствии с табл. 7
Таблица 7
|
Адрес ячейки |
Выражение |
|
M5 |
=J5*I5 |
|
M6 |
=J6*I6 |
|
M7 |
=J7*I7 |
|
M8 |
=J8*I8 |
|
M9 |
=J9*I9 |
|
M10 |
=J10*I10 |
|
M11 |
=J11*I11 |
|
M12 |
=J12*I12 |
|
M13 |
=J13*I13 |
|
M14 |
=J14*I14 |
|
M15 |
=J15*I15 |
|
M16 |
=J16*I16 |
|
M17 |
=СУММ(М5:М16) |
Затраты на закупку каждого компонента шихты на весь объем завалки (6 тонн) определяются путем умножения цены материала на его количество (в тоннах). Затраты на закупку каждого компонента шихты в грн. будут представлены в диапазоне ячеек N5:N16, а сумма затрат на закупку всего объема шихтовых материалов в ячейке N17. Для выполнения расчетов водим формулы в соответствии с табл. 8.
Таблица 8
|
Адрес ячейки |
Выражение |
|
N5 |
=(L5*I5)/1000 |
|
N6 |
=(L6*I6)/1000 |
|
N7 |
=(L7*I7)/1000 |
|
N8 |
=(L8*I8)/1000 |
|
N9 |
=(L9*I9)/1000 |
|
N10 |
=(L10*I10)/1000 |
|
N11 |
=(L11*I11)/1000 |
|
N12 |
=(L12*I12)/1000 |
|
N13 |
=(L13*I13)/1000 |
|
N14 |
=(L14*I14)/1000 |
|
N15 |
=(L15*I15)/1000 |
|
N16 |
=(L16*I16)/1000 |
|
N17 |
=СУММ(N5:N16) |
В ячейку J18 вносим значение целевой функции. Это значение определим с использованием встроенной математической функции СУММПРОИЗВ(1-й массив; 2-й массив). Первый массив состоит из значений цены каждого компонента шихты (диапазон ячеек I5:I16), второй массив - из значений переменных Х1, …, Х12 (диапазон ячеек J5:J16). Таким образом, в ячейку J18 необходимо ввести следующее выражение =СУММПРОИЗВ(I5:I16;J5:J16).
В ячейку К26, которая будет отражать ожидаемое содержание углерода в чугуне, вводим левые части неравенств (3) и (4). Для этого в данную ячейку вводим математическую функцию =СУММПРОИЗВ(D5:D16;$J$5:$J$16).
В ячейку L26, которая будет отражать ожидаемое содержание кремния в чугуне, вводим левые части неравенств (5) и (6). Для этого в данную ячейку вводим функцию =СУММПРОИЗВ(E5:E16;$J$5:$J$16).
В ячейку M26, которая будет отражать ожидаемое содержание марганца в чугуне, вводим левые части неравенств (7) и (8). Для этого в данную ячейку вводим функцию =СУММПРОИЗВ(F5:F16;$J$5:$J$16).
В ячейку N26, которая будет отражать ожидаемое содержание фосфора в чугуне, вводим левую часть неравенства (9). Для этого в данную ячейку вводим функцию =СУММПРОИЗВ(G5:G16;$J$5:$J$16).
В ячейку O26, которая будет отражать ожидаемое содержание серы в чугуне, вводим левую часть неравенства (10). Для этого в данную ячейку вводим функцию =СУММПРОИЗВ(Н5:Н16;$J$5:$J$16).
ПОИСК РЕШЕНИЯ
Дальнейшие действия: в меню Сервис выбираем команду Поиск решения. В появившемся диалоговом окне (см. рис. 4) заполняем соответствующие поля по следующей схеме:
· Установить целевую ячейку - вводим адрес ячейки целевой функции (целевой ячейки). В нашем случае это ячейка М18. Следовательно в это поле вводим значение $M$18.
· Равной: максимальному значению, конкретному значению, минимальному значению. Данное поле определяет тип оптимизации (искать максмум, минимум или конкретное значение функции). Наша задача определить состав компонентов шихты с минимальной стоимостью, поэтому устанавливаем флажок в этом поле на отметке - "минимальному значению".
· Изменяя ячейки. Т.к. мы ищем минимум функции изменяя содержание компонентов шихты, которые приведены в диапазоне ячеек J5чJ16, то в данное поле вводим следующее выражение $J$5:$J$16.
· Ограничения. В данное поле вводим линейные ограничения (3) - (24). При задании системы ограничений используется кнопка Добавить. При её нажатии появляется вспомогательное диалоговое окно, в поля которого вводятся ссылки на ячейки и ограничения, накладываемые на переменные в рассматриваемой задаче. Как видно на рис. 4 , сформированную систему ограничений в дальнейшем можно редактировать. Для этого служат кнопки Изменить и Удалить.
Рисунок 4

Рассмотрим подробно каждое ограничение:
Неравенство (3) - ограничивает нижний предел содержания углерода в чугуне. Левая часть неравенства в таблице Excel отражается в ячейке К26, а правая часть неравенства в ячейке К21. Следовательно для оформления ограничения, предусмотренного неравенством (3), необходимо произвести следующие действия. В меню Поиск решения нажимаем кнопку Добавить, открывается меню Добавление ограничения (см. рис. 5), в поле Ссылка на ячейку вводим адрес ячейки, в которой производится суммирование содержания углерода в чугуне, т.е. $K$26; в поле математической операции вводим знак неравенства >=; в поле Ограничение вводим минимальнодопустимое содержание углерода в чугуне с учетом угара, значение которого рассчитано и приведено в ячейке $K$21; нажимаем кнопку Добавить, ограничение введено.
Рисунок 5
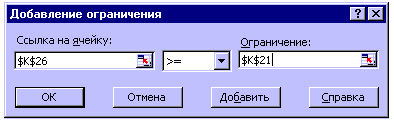
Неравенство (4) - ограничивает верхний предел содержания углерода в чугуне. Оформление огра-ничения осуществляем в той же последовательности. В меню Поиск решения нажимаем кнопку Добавить, открывается меню Добавление ограничения, в поле Ссылка на ячейку вводим адрес ячейки, в которой производится суммирование содержания углерода в чугуне, т.е. $K$26; в поле математической операции вводим знак неравенства <=; в поле Ограничение вводим максимальнодопустимое содержание углерода в чугуне с учетом угара, значение которого рассчитано и приведено в ячейке $K$22; нажимаем кнопку Добавить, ограничение введено.
Дальнейшие действия по вводу ограничений понятны, поэтому приводим только конкретные выражения, вводимые в соответствующие ячейки.
Неравенство (5) - $L$26 >= $L$21.
Неравенство (6) - $L$26 <= $L$22.
Неравенство (7) - $M$26 >= $M$21.
Неравенство (8) - $M$26 <= $M$22.
Неравенство (9) - $N$26 <= $N$22.
Неравенство (10) - $O$26 <= $O$22.
Равенство (11) - определяет сумму компонентов шихты, равной (в относительных единицах) 1. Суммирование компонентов шихты производится в ячейке J17, следовательно, для оформления данного ограничения мы должны ввести в соответствующие поля меню Добавление ограничения следующее выражение $J$17 = 1.
Равенство (12) - ограничивает количество используемого возврата. Содержание возврата в соста-ве шихты приведено в ячейке J14, следовательно, вводим выражение $J$14 = 0,34.
Все последующие неравенства оформляем по той же схеме.
Неравенство (13) - $J$13 >= 0.
Неравенство (14) - $J$13 <= 0,08.
Неравенство (15) - $J$5 >= 0.
Неравенство (16) - $J$6 >= 0.
Неравенство (17) - $J$7 >= 0.
Неравенство (18) - $J$8 >= 0.
Неравенство (19) - $J$9 >= 0.
Неравенство (20) - $J$10 >= 0.
Неравенство (21) - $J$11 >= 0.
Неравенство (22) - $J$12 >= 0.
Неравенство (23) - $J$15 >= 0.
Неравенство (24) - $J$16 >= 0.
Все предусмотренные ограничения введены и теперь можно найти оптимум функции. Для этого в меню Поиск решения нажимаем на кнопку Выполнить, после чего будет осуществлена процедура Поиск решения, по результатам которой выводится сообщение о найденном решении.
Полученные результаты можно сохранить (кнопка ОК); можно также отказаться от сохранения результатов (кнопка Отмена).
Таким образом, получили искомое решение сформулированной задачи оптимизации: из имеющихся (согласно принятым условиям задачи) 16 компонентов шихты, предназначенных для получения серого чугуна марки СЧ20, программа выбрала состав шихты (в процентах и кг), обеспечивающий мини-мальную стоимость затрат на их закупку - 1845,848 грн. за 6 т шихтовых материалов или 307,6414 грн. за 1 т.
Формат сайта не позволяет расписать подробно все тонкости приводимой методики, но хочется отметить, что если произвести тот же расчет, но в условиях задачи поставить условие - максимум стоимости шихты, то получим состав завалки, стоимость которой составит - 3696,39 грн. за 6 т или 616,065 грн. за 1 т. Следовательно, из одного набора шихтовых материалов можно выплавить чугун, практически одного состава, но при этом затраты на его производство (по шихтовым материалам), могут отличаться в два раза!
Выводы:
· При разработке норм расхода шихтовых материалов и осуществлении закупок шихтовых материалов технологам и менеджерам целесообразно использовать приведенную методику оптимизации состава шихты. Это особенно актуально при производстве многокомпонентных сплавов и при больших потоках производства, экономия может быть очень значительна.
· Описанная методика построена на использовании электронных таблиц Excel, обладающих мощным встроенным математическим аппаратом, что обеспечивает поиск решения при использовании любого количества компонентов шихты и проведении расчетов на практически любое количество элементов, получаемого сплава.