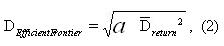http://www.mirkin.ru/_docs/articles03-052.pdf
Корреляционная матрица и ее роль в оптимизации
фондового портфеля
Бессонов Дмитрий Николаевич, SBS Russia, инженер-программист
Недосекин Алексей Олегович, SBS Russia, старший консультант, канд. техн. наук
Хорошо известно, что в классической задаче оптимизации фондового
портфеля по методу Марковица участвует корреляционная матрица активов.
Доказано [1], что погрешность в определении параметров корреляционной
матрицы воздействует на точность решения задачи на порядок слабее, нежели
параметры доходностей и рисков активов. Докажем это же свойство
«информационной незначительности» корреляционной матрицы, когда ставится и
решается задача Марковица в нечеткой постановке [2].
Пусть заданы треугольные вектора доходностей и риска активов и
треугольная корреляционная матрица активов. Решением задачи оптимизации в
этой постановке является эффективная граница портфельного множества в форме
криволинейной полосы [2,3] с верхней и нижней границами.
Вполне понятно на сегодняшний день, как верифицировать треугольную
оценку доходности и риска актива. Самое целесообразное . это интерпретировать
тренд актива по формуле конечной доходности:
S(t) = S(0) * (1 + r*t)
(1)
где r . случайная величина доходности актива, имеющая нормальное
двупараметрическое распределение с нечеткими параметрами. Устанавливая
уровень функции правдоподобия при анализе исторических ценовых данных, мы
можем получить соответствующую этому уровню треугольную оценку [2]. И, чем
ниже уровень правдоподобия, тем шире уровень размытия оценки.
Что же касается оценки параметров треугольной корреляционной матрицы,
то мы не можем применить к этой оценки метод, описанный выше, т.к. оценивается
не случайный процесс, а некая свертка совокупности самих этих процессов. В этой
ситуации наравне с вопросом о методике размытия встает вопрос о том, насколько
сильно размытие влияет на решение задачи оптимизации. Спросим себя, в каких
пределах мы можем безбоязненно менять корреляцию активов интересующего нас
портфеля, не рискуя стабильностью решения.
Для верификации параметров треугольной матрицы мы использовали
хорошо известный способ вариации параметров. Суть его в следующем.
Для начала определим критерий стабильности решения . меру похожести
решений оптимизации. Пусть, нам даны две эффективные границы. Разделив
линию эффективной границы по координатной оси рисков на некоторое
количество равных частей, мы получим набор контрольных точек (в расчетах
использовалось 10), в которых будем замерять расхождения значений риска на этих
двух эффективных границах. Для того, чтобы получить скалярный показатель
расхождения, который можно будет сравнивать с заданным порогом подобия,
используем следующую формулу.
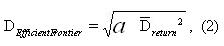
где Dreturn - осредненное по контрольным точкам значение
расхождений
доходности.
Предложенный способ оценки чувствительности эффективной границы к
колебаниям исходных данных удобен тем, что оценка расхождения решений
оптимизации становится «одномерной». Варьируя параметрами корреляционной
матрицы, мы ищем такие границы этих параметров, при которых ошибка решения,
оцениваемая (2) не превышает заранее установленного уровня. В этом и суть
предлагаемого метода «фузификации» корреляционной матрицы.
Сначала для примера проведем оптимизацию портфеля из трех активов.
Были выбраны модельные активы, использующиеся в программном продукте
«Система портфельной оптимизации» компании Siemens Business Services Russia.
Ими стали:
·
Rus Govt - Государственные ценные бумаги РФ, модельный актив построен
на базе индекса SBS Rus Govt (разработанный SBS индекс российских
государственных облигаций);
·
Rus Muni - Государственные ценные бумаги субъектов РФ, модельный
актив построен на базе индекса SBS Rus Muni (разработанный SBS индекс
облигаций субъектов РФ);
·
Rus Stocks 1 - Акции российских эмитентов (первый эшелон), модельный
актив построен на базе индекса SBS Rus Corp (разработанный SBS индекс
корпоративных российских облигаций по данным ММВБ).
Мы имеем матрицу 3 на 3, с тремя элементами, поддающимися
корректировке в пределах [-1, 1] (клетки зеленого цвета)
Удобство набора из трех активов состоит в том, что область всех возможных
значений корреляционной матрицы представляет из себя трехмерный куб с ребром
равным единице и центром в точке начала координат. В нашей матрице каждой из
варьируемых клеток будет логично сопоставить свою координатную ось.
Назовем базовой точкой в пространстве значений корреляционной матрицы
значение корреляции, посчитанное стандартными методами. Решение задачи
оптимизации (эффективная граница) полученное в этой точке, назовем базовым.
Произведем оценку расхождения решений от базового при варьировании
значений корреляции по каждой из осей по отдельности, оставляя два других
значения корреляции в базовой точке. В этом случае мы делаем срез куба
значений
двумя плоскостями, параллельными сторонам куба; получаем отрезок, в каждой
точке которого считаем отклонение решения от базового. Контрольными
пороговыми значениями будут 0,2% и 0,5%, оцениваемые по (2). Определим
границы области стабильности решения оптимизации.
·
Для пары Rus Govt - Rus Muni (рис. 1)
Rus Govt - Rus Muni
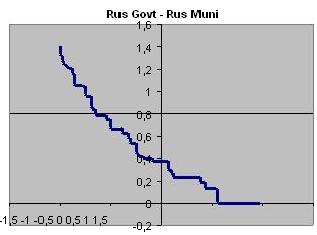
Для порога 0,50%
Минимум
-0,24
Контрольная
0,94
Максимум
1
Для порога 0,20%
Минимум
0,39
Контрольная
0,94
Максимум
1
Рис. 1. Определение чувствительности корреляционного коэффициента для
пары Rus Govt - Rus Muni
·
Для пары Rus Govt - Rus Stocks 1 (рис. 2)
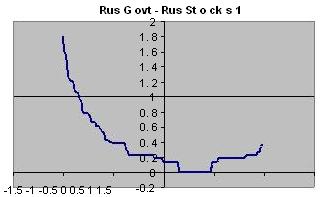
Для порога 0,50%
Минимум
-0,587
Контрольная
0,263
Максимум
1
Для порога 0,20%
Минимум
-0,097
Контрольная
0,263
Максимум
0.8
Рис. 2. Определение чувствительности корреляционного коэффициента для
пары Rus Govt - Rus Stocks 1
·
Для пары Rus Muni - Rus Stocks 1 (рис. 3)
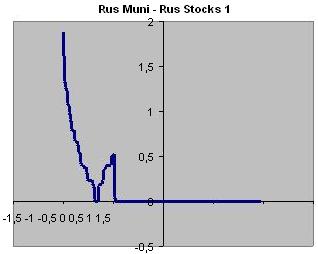
Для порога 0,50%
Минимум
-0,483
Контрольная
0,017
Максимум
1
Для порога 0,20%
Минимум
-0,483
Контрольная
0,017
Максимум
1
Рис. 3. Определение чувствительности корреляционного коэффициента для
пары Rus Muni - Rus Stocks 1
Более зрелищным будет совместное варьирование двух элементов
корреляционной матрицы. В этом случае происходит срез куба одной плоскостью,
зафиксированной на уровне базового значения корреляции оставшейся пары.
Получаем квадратную площадку значений отклонения решения от базового. Будем
считать значение отклонения решения от базового высотой поверхности в этой
точке. Построим карту высот на поверхности квадрата (рис. 4).

Рис. 4. Двухмерное варьирование параметров корреляционной матрицы
На графике поверхности рис. 4 хорошо видна зона устойчивости решения
(ближайший к нам угол координатной плоскости).
Теперь рассмотрим случай портфеля из 10 активов. Для каждой пары
приведем одномерный срез . варьируется корреляция между взятыми активами,
вся прочая матрица является базовой. В задачу добавлены следующие модельные
активы:
·
Rus Govt - Государственные ценные бумаги РФ, модельный актив построен
на базе индекса SBS Rus Govt (разработанный SBS индекс российских
государственных облигаций);
·
Rus Muni - Государственные ценные бумаги субъектов РФ, модельный
актив построен на базе индекса SBS Rus Muni (разработанный SBS индекс
облигаций субъектов РФ);
·
Rus Bonds - Облигации российских эмитентов, модельный актив построен
на базе индекса SBS Rus Corp (разработанный SBS индекс корпоративных
российских облигаций)
·
Rus Stocks 1 - Акции российских эмитентов (первый эшелон), модельный
актив построен на базе индекса РТС;
·
Rus Stocks 2 - Акции российских эмитентов (второй эшелон), модельный
актив построен на базе индекса AK&M-2 (индекс агентства AK&M,
отражающий динамику российских акций второго эшелона);
·
USA Govt - Государственные ценные бумаги США, модельный актив
построен на базе индекса TYX RUR Cum (кумулятивный индекс 30-летних
облигаций правительства США по данным Федеральной резервной системы
США, в рублевой котировке);
·
USA Bonds - Корпоративные облигации США, модельный актив построен
на базе индекса Moody AAA RUB Cum (кумулятивный индекс
американских корпоративных облигаций агентства Moody's, в рублевой
котировке);
·
USA Stocks - Акции эмитентов США, модельный актив построен на базе
индекса S&P500 RUB (индекс акций агентства S&P, в рублевой котировке);
·
Euro Govt - Облигации европейских государств, модельный актив построен
на базе индекса BE Gilts RUB Cum (кумулятивный индекс доходности по
государственным облигациям Великобритании, по данным Банка Англии, в
рублевой котировке);
·
Euro CD - Банковские депозиты европейских государств, модельный актив
построен на базе индекса BE CD RUB Cum (кумулятивный индекс
доходности по банковским депозитам Великобритании, по данным Банка
Англии, в рублевой котировке).
Результаты вариационного анализа для уровня предельной ошибки решения
приведены в табл. 1. Видно, что разброс корреляции, сохраняющий четкость
решения оптимизации с заданной точностью соответствия весьма широк, т. е.
пределы невосприимчивости решения к размытию корреляционной матрицы
отстоят от базовой точки корреляции достаточно далеко. Это позволяет говорить о
том, что при решении задачи оптимизации в нечеткой постановке присутствует
значительная вольность при размытии корреляционной матрицы. Более того: нам
вообще необязательно размывать матрицу, потому что эффект от размытия не
будет заметным (на фоне существенных размытий доходности и риска активов).
Это позволяет нам целиком сосредоточиться на более тщательном
прогнозировании параметров доходности и риска активов портфеля. Чем точнее
мы их спрогнозируем, тем уже будет разброс полосы эффективной границы, тем
более похожим на классическое будет решение задачи Марковица.
Таблица 4. Треугольные оценки параметров корреляционной матрицы
Оценка коэффициента корреляции
Пары активов Минимум Базовая
Максимум
Rus Govt - Rus Muni -0,990 0,940
1,000
Rus Govt - Rus Bonds -0,990 0,950
1,000
Rus Govt - Rus Stocks 1 -0,997 0,263
0,993
Rus Govt - Rus Stocks 2 -0,360 0,640
1,000
Rus Govt - USA Govt -0,991 -0,411
0,999
Rus Govt - USA Bonds -0,992 -0,412
0,998
Rus Govt - USA Stocks -0,975 0,055
0,995
Rus Govt - Euro Govt -0,997 -0,337
0,993
Rus Govt - Euro CD -0,998 -0,338
0,992
Rus Muni - Rus Bonds -0,990 0,940
1,000
Rus Muni - Rus Stocks 1 -0,993 0,017
0,997
Rus Muni - Rus Stocks 2 0,075 0,775
0,995
Rus Muni - USA Govt -0,993 -0,663
0,627
Rus Muni - USA Bonds -0,996 -0,666
0,994
Rus Muni - USA Stocks -0,998 -0,238
0,992
Rus Muni - Euro Govt -0,995 -0,565
0,995
Rus Muni - Euro CD -0,996 -0,566
0,994
Rus Bonds - Rus Stocks 1 -0,997
0,263 0,993
Rus Bonds - Rus Stocks 2 -0,450
0,640 1,000
Rus Bonds - USA Govt -0,991 -0,411
0,999
Rus Bonds - USA Bonds -0,912 -0,412
0,998
Rus Bonds - USA Stocks -0,985 0,055
0,995
Rus Bonds - Euro Govt -0,997 -0,337
0,993
Rus Bonds - Euro CD -0,998 -0,338
0,992
Rus Stocks 1 - Rus Stocks 2 -0,575
0,075 0,995
Rus Stocks 1 - USA Govt -0,327 0,463
0,973
Rus Stocks 1 - USA Bonds -0,614
0,466 0,996
Rus Stocks 1 - USA Stocks -0,843
0,677 0,997
Rus Stocks 1 - Euro Govt -0,636
0,414 0,994
Rus Stocks 1 - Euro CD -0,908 0,412
0,992
Rus Stocks 2 - USA Govt -0,992
-0,732 -0,432
Rus Stocks 2 - USA Bonds -0,941
-0,711 0,999
Rus Stocks 2 - USA Stocks -0,985
-0,515 0,995
Rus Stocks 2 - Euro Govt -0,941
-0,631 0,999
Rus Stocks 2 - Euro CD -0,858 -0,628
0,992
USA Govt - USA Bonds -0,224 0,996
0,996
USA Govt - USA Stocks -0,267 0,823
0,993
USA Govt - Euro Govt -0,358 0,932
0,992
USA Govt - Euro CD -0,358 0,932
0,992
USA Bonds - USA Stocks -0,067 0,793
0,993
USA Bonds - Euro Govt 0,126 0,946
0,996
USA Bonds - Euro CD 0,156 0,946
0,996
USA Stocks - Euro Govt -0,196 0,714
0,994
USA Stocks - Euro CD -0,140 0,710
1,000
Euro Govt - Euro CD -0,990 1,000
1,000
Список цитируемых источников
1.Chopra V.K., Ziemba W.T. The Effects of Errors in Means, Variances, and
Covariances on Optimal Portfolio Choice. . In: Worldwide Asset And Liability
Modeling.. Cambridge University Press, 1998.
2.Недосекин А.О. Нечетко-множественный анализ риска фондовых инвестиций. -
СПб.: изд. Сезам, 2002. [http://sedok.narod.ru/sc_group.html]
3.Недосекин А.О. Оптимизация модельных фондовых портфелей в условиях
существенной неопределенности // Аудит и финансовый анализ. . 2002. - № 1.
[http://sedok.narod.ru/sc_group.html]