Genetic Programming

Evolutionary Computation - Lecture 15

22/11/2002

Thorsten Schnier

School of Computer Science

University of Birmingham

Previous Lecture

Constraint Handling

Penalty Approach

Penalize fitness for infeasible solutions, depending on distance from feasible region

Balanace between under- and over-penalization

Static, dynamic, and adaptive

Repair Approach

Use feasible reference individuals to move infeasible points

Other approaches

Genetic Programming (GP)

Two different view of what GP means:

Content view: Automatic Programming

Creation of programs by artificial evolution

Different representations

Representation view: anything using tree representation

May be programs, may be other things

Representing Programs in EC

Tree representation

LISP-like expression

Local data storage

Tree Genotypes

Tree genetic operators

Linear representation

Series of instructions

Registers for data storage

Graph representation

Nodes contain instructions

Edges control program flow

Stack for data storage

Example Problem: Symbolic Regression

Example Problem: Symbolic Regression

Given: a set of function points

Problem: find a function that fits the points as closely as possible

Common problem in stats, process engineering, ...

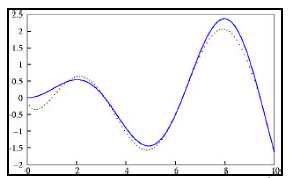
Tree Representation for Symbolic Regression

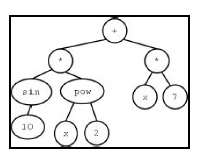
Terminal Set and Function Set

The Terminal Set

Anything with arity 0 and one output

Arity: number of inputs (unary, binary, ...)

Inputs

Sensors

Function variables

Constants

Numbers

Do we need to supply all possible constants ?

The Function Set

n-ary functions

E.g. mathematical functions +, -, *, /, log, sum, ...

E.g. boolean functions and, or, not, xor, ...

E.g. memory functions store, read

E.g. control structures if..then..else, for, ...

E.g. side-effect functions move, pen up, turn, ...

Sufficiency

need a set of functions sufficiently complex for the task

but not too rich

Coverage

Functions need to be defined over all inputs

E.g. division needs to be defined for input 0

Crossover

Branch Swap

Pick random branch at both parents

Swap branches

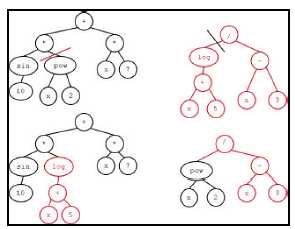
Matched One-point Tree Crossover

Matching

From root follow branches

As long as nodes have same arity

Same crossover point for both parents, within matched branches

n-point crossover possible, too

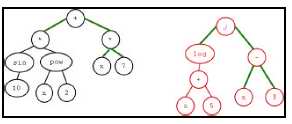
Advantages and Disadvantages

Does not change tree depth

Less disruptive

Population more likely to converge

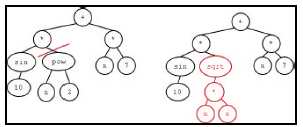
Mutation

Branch replacement

Pick random branch from parent

Delete branch

Replace with random new branch

(New branch created as in initial population creation)

Creation of Initial Population

Bloat

Program size grows

As a result of uneven crossover

Unused code

Slows down runs

More space, cpu time required

Mutation, crossover of unused code - offspring behaviour is identical

Countermeasures

Incorporate program size into fitness

Use special crossover (e.g. matched one-point crossover)

Linear Representation Genetic Programming

Register Machine

Van-Neuman Architecture

String of instructions and data

Functions get arguments from registers

String Representation

Usually variable-length

Crossover: variable-length versions of one-pint, two-point

Mutation: ’usual’ random gene replacement, but also add, delete operations

Graph Representation Genetic Programming

Nodes define operations

Operands come from stack

Result will be put onto the stack

Edges define control flow

Control mechanism controls which edge to follow

E.g. depends on value written to stack {<0, =0, >0}

Loops and recursion common

Specialized Crossover and Mutation operators

Genetic Programming == Automatic Programming ?

Does it start from a high level specification ?

Does it produce an executable program ?

Does it automatically deteremine the number of steps a program should take ?

Does it produce results that are competitive with human programmers, engineers, mathematicians and designers ?

Genetic Programming Applications

Regression

Chemistry,Engineering

Statistics

Classification etc.

Data Mining

Intrusion Detection

Image classification

Control

Plants

Robots

Spacecraft altitude maneuvres

Animation

Design

Neural Networks

Electronic Circuits

Sumary

Automatic Generation of Programs

within limits...

Tree Representation

Tree crossover

Branch replacement mutation

Other Representations

Linear

Graph

References

Basic Reading:

Wolfgang Banzhaf, Peter Nordin, Robert E. Keller, and Frank D.

Francone Genetic Programming: An Introduction Morgan

Kaufmann Publishers (In the Library): Chapter 5

Advanced Reading

Other chapters in Banzhaf et. al

John R. Koza: Genetic Programming: On the Programming of Computers by Means of Natural Selection (In the library - don’t be put off by the volume of the book, you can skim over a lot of the material quickly, just pick interesting applications.)

Websites

http://www.genetic-programming.com/