NFV-подход к оцениванию инвестиционных проектов
Шубин Д.А.
Новосибирский государственный технический университет (Новосибирск)
Кратко о подходе
Метод NFV (Net Future Value) – это оригинальный подход к оцениванию эффективности инвестиционного проекта [1]. Значением NFV является доход, получаемый от проекта на конец его реализации. При вычислении NFV применяются два вида ставок: ставка кредита и ставка, под которую вкладываются временно свободные средства (доходы второго уровня). NFV учитывает эти доходы второго уровня, а также реинвестирование в проект (средства на инвестирование в проект будут вводиться (передаваться) из доходов других или этого же проектов; в этом случае средства не обязательно должны быть в наличии на момент начала реализации проекта). Подобные и другие методы оптимизации дохода позволяют увеличить его значение, но уже на этапе оценки (предварительной), не разработки.
Внутренняя норма доходности на основе NFV – такое значение ставки кредита, при которой значение NFV обращается в нуль. Такая норма доходности показывает реальную (максимальную) границу доходности (в процентах) от использования инвестиций.
Срок окупаемости – продолжительность периода от начального момента до момента окупаемости. Момент окупаемости – наиболее ранний момент времени, после которого NFV становится и в дальнейшем остается неотрицательным. Поскольку зачастую значение NFV проекта больше, чем “обычный”, “не оптимизированный” чистый доход, то и срок окупаемости на основе NFV-подхода меньше, чем “обычный” срок окупаемости.
Модификации NFV
Перечислим некоторые из возможных модификаций расчета NFV.
1. Первая модификация предполагает, что в инвестиционный проект вкладываются исключительно собственные средства. Тогда расчет NFV1 осуществляется по следующей формуле:
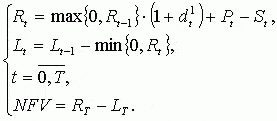
Здесь приняты следующие обозначения:
- R - отдача от проекта,
- L - заемные средства,
- T - время окончания инвестиционного проекта,
- d1 - банковская депозитная ставка процента.
2. Вторая модификация. Вкладываются заемные средства, которые нужно возвратить в конце жизненного цикла проекта. И NFV2 можно рассчитать по формуле:
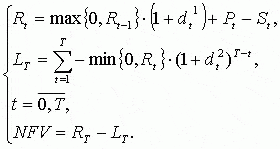
Дополнительные обозначения:
- d2 - ставка заимствования или ставка процента, под который взят кредит.
3. Наконец, вкладываемые заемные средства возвращаются по выгодной для заемщика схеме возврата, т.е. заемщик пытается погасить в первую очередь самый обременительный кредит, и, если ставка банковского депозита больше, чем ставка заимствования, то кредит не погашает, а держит накопленные средства в банке. Из-за означенных условий, формула для расчета NFV3 является довольно громоздкой.
Примечание: во всех случаях предполагаем, что полученные от проекта средства хранятся на одном депозитном счете в банке.

Здесь использованы новые обозначения:
- L1 – кредит,
- d21 – ставка процента для кредита L1,
- Сt – накопленный доход от проекта на момент времени t.
Примечание:
- Через вычисление значения
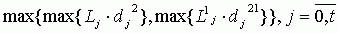 происходит выбор самого обременительного кредита к моменту времени t.
происходит выбор самого обременительного кредита к моменту времени t. - Сравнение
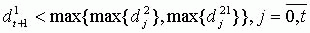 необходимо для проверки: меньше ли ставка процента на расчетном счете, чем проценты взятых
ранее кредитов.
необходимо для проверки: меньше ли ставка процента на расчетном счете, чем проценты взятых
ранее кредитов. - Сумма
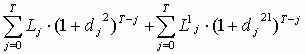 - это невозвращенные долги L и L1 к моменту времени T.
- это невозвращенные долги L и L1 к моменту времени T.
Функциональная схема NFV3 (рисунок 1) наглядно изображает работу алгоритма.

Рисунок 1 – Функциональная схема расчета NFV3 (третья модификация)
Каждый период начинается с проверки: нужно ли вкладывать в проект в этом периоде. Если да, то выбирается источник финансирования: - либо собственные средства, - либо заемные. И производится очередное вложение. Далее, если остались средства, то погашаются кредиты, и погашаются в первую очередь самые обременительные. И так далее от периода к периоду идет работа по означенной схеме.
Реальный пример. С оценкой эффективности данного проекта столкнулся один из Новосибирских банков. В своих расчетах они использовали NPV критерий. Применим к исходным данным подход NFV (рисунок 2).
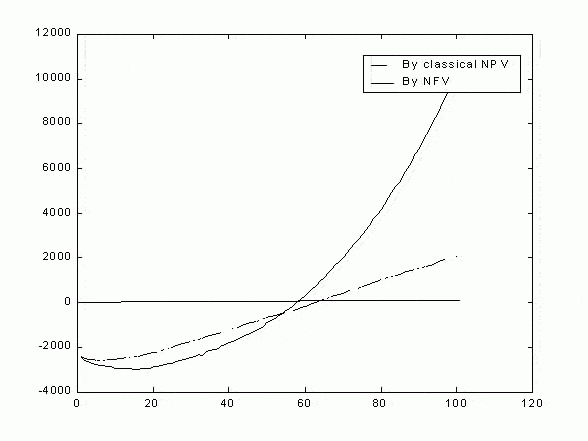
Рисунок 2 – Результат расчета NFV3 (третья модификация) и NPV
На графике ось абсцисс – ось времени, а ордината – доход от проекта. Непрерывная кривая - это NFV, пунктирная – NPV. По NFV проект окупится быстрее, к тому же кривая дохода на много круче.
На рисунке 3 показана плотность вероятности NPV, NFV. Было выполнено тысяча просчетов при нестабильных ставках кредита и банковского депозита, что и привело к разбросу значений. Имеем, что NFV более чувствителен к изменению ставок.

Рисунок 3 – Плотность вероятности NPV, NFV
Риски
Для того чтобы оценить риски проводится множество просчетов проекта, изменяя его параметры, чаще значения ставок кредита и ставок, под которые вкладываются временно свободные средства проекта. В итоге получается множество возможных значений NFV проекта. И выдвигаются возможные подходы к оцениванию рисков, соответствующих подходу NFV [2, 3]:
- Отклонение среднего значения (NFV0) от минимального (NFVmin), т.е. максимальные потери (R1NFV).
- Разность между NFV0 и средним значением NFV (при отклонении NFV от NFVmin до NFV0), т.е. средние потери (R2NFV).
- Относительные наибольшие потери, полученные на основе R1NFV (R3NFV, в процентах).
- Относительные средние потери (R4NFV, в процентах).
Значение R2 является более устойчивым к изменению параметров инвестиционного проекта, чем R1, так как является разностью средних величин, поэтому риск R2 используется как основная величина риска проекта.
Рассмотрим пример проекта. Пусть потоки проекта имеют вид, представленный в таблице 1. Здесь 10 периодов, S(t) – входной поток проекта, P(t) – выходной поток.
Существует несколько схем использования заемных средств и расчета по долгам. Первая схема – без заимствований с внутренним перераспределением средств (первая модификация NFV). Вторая – в проект вкладываются уже только заемные средства, которые нужно возвратить по окончании жизни проекта (вторая модификация NFV). Третья – вкладываются заемные средства, возвращаемые по мере поступления доходов от проекта (третья модификация NFV). Очевидно, что последняя схема более приближена к реальности, будем рассчитывать значение NFV по ней.
Таблица 1 – Входные и выходные потоки проекта
| T | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| S(t) | 100 | 150 | 0 | 30 | 0 | 60 | 0 | 10 | 25 | 0 |
| P(t) | 0 | 15 | 150 | 560 | 80 | 45 | 0 | 200 | 100 | 120 |
Длительность одного временного такта составляет один год. Оценим риски в предположении, что параметры NFV нестабильны. Так, пусть d10 – математическое ожидание значения банковского депозита, d20 – математическое ожидание ставки кредита, а σ d10 и σ d20 – соответствующие средние квадратические отклонения и имеет место нормальный закон распределения параметров d1 и d2. На рисунке 4 показан один из возможных видов плотности вероятностей для NFV в этом случае.

Рисунок 4 – Плотность вероятности значений NFV3
Значения рисков при разных значениях параметров и для 1000 модельных просчетов приведены в таблице 2.
Таблица 2 – Значения рисков при различных параметрах
| N п/п | Параметры | Риски | ||||||
| d10, % | d20, % | σ d10 | σ d20 | R1NFV | R2NFV | R3NFV, % | R3NFV, % | |
| 1 | 18 | 25 | 0.01 | 0.01 | 59.145 | 18.945 | 4.0418 | 1.2946 |
| 2 | 17 | 25 | 0.01 | 0.01 | 72.894 | 19.270 | 5.1695 | 1.3666 |
| 3 | 16 | 25 | 0.01 | 0.01 | 90.974 | 18.270 | 6.6849 | 1.3797 |
| 4 | 18 | 26 | 0.01 | 0.01 | 64.651 | 20.083 | 4.4659 | 1.3872 |
| 5 | 18 | 27 | 0.01 | 0.01 | 77.242 | 20.240 | 5.4014 | 1.4153 |
| 6 | 16 | 27 | 0.01 | 0.01 | 62.603 | 17.737 | 4.7195 | 1.3372 |
| 7 | 18 | 25 | 0.02 | 0.01 | 133.58 | 35.790 | 9.1176 | 2.4429 |
| 8 | 18 | 25 | 0.01 | 0.02 | 102.55 | 30.069 | 7.0003 | 2.0525 |
| 9 | 18 | 25 | 0.02 | 0.02 | 152.30 | 39.678 | 10.407 | 2.7112 |
Сделаем некоторые выводы. С уменьшением ставки на депозитном счете (п/п 1 – 3 в таблице 2) увеличивается отклонение среднего значения от минимального (максимальные потери) – “колокол” плотности вероятности расширяется. Средние же потери колеблются около 19 денежных единиц. Увеличение ставки кредита приводит к незначительному увеличению рисков (п/п 4, 5). В п/п 6 для инвестора представлены заведомо невыгодные параметры (на депозитном счете наименьший процент из рассматриваемых в примере и наибольшая ставка банковского процента), что чаще приводит к одному значению критерия без каких-либо разбросов. При увеличении квадратических отклонений риски резко повышаются – “колокол” плотности вероятности все больше расширяется, т.к. повышается разброс значений ставок банковского кредита и на депозитном счете.
Пусть потоки очередного проекта имеют вид, представленный в таблице 3, в таблице 4 – соответствующие значения рисков.
Таблица 3 – Входные и выходные потоки проекта
| T | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| S(t) | 100 | 150 | 0 | 20 | 0 | 20 | 0 | 10 | 25 | 0 |
| P(t) | 0 | 65 | 65 | 70 | 75 | 80 | 90 | 100 | 100 | 105 |
Таблица 4 – Значения рисков при различных параметрах
| N п/п | Параметры | Риски | ||||||
| d10, % | d20, % | σ d10 | σ d20 | R1NFV | R2NFV | R3NFV, % | R3NFV, % | |
| 1 | 18 | 25 | 0.01 | 0.01 | 64.9220 | 16.9927 | 47.0414 | 12.3127 |
| 75.9836 | 16.3669 | 55.5327 | 11.9617 | |||||
| 64.2508 | 16.6231 | 46.4845 | 12.0266 | |||||
| 2 | 17 | 25 | 0.01 | 0.01 | 81.0520 | 16.5112 | 59.0332 | 12.0257 |
| 70.8412 | 17.1732 | 51.5323 | 12.4875 | |||||
| 75.5584 | 15.7074 | 55.3941 | 11.5156 | |||||
| 3 | 16 | 25 | 0.01 | 0.01 | 63.9958 | 16.1137 | 46.3855 | 11.6795 |
| 75.5077 | 17.1581 | 54.8232 | 12.4578 | |||||
| 63.6106 | 15.7886 | 46.5406 | 11.5517 | |||||
| 4 | 18 | 26 | 0.01 | 0.01 | 73.8490 | 17.9629 | 74.9484 | 18.2303 |
| 78.2797 | 19.3416 | 79.5355 | 19.6519 | |||||
| 76.6343 | 18.9532 | 76.1142 | 18.8245 | |||||
| 5 | 18 | 27 | 0.01 | 0.01 | 82.2960 | 20.5574 | 149.8527 | 37.4329 |
| 155.3529 | 21.0026 | 276.9817 | 37.4459 | |||||
| 90.8995 | 20.6947 | 170.3023 | 38.7720 | |||||
| 6 | 16 | 27 | 0.01 | 0.01 | 79.2840 | 20.1879 | 143.4749 | 36.5327 |
| 88.2492 | 19.9000 | 156.8653 | 35.3728 | |||||
| 101.8517 | 19.9529 | 183.9016 | 36.0266 | |||||
| 7 | 18 | 25 | 0.02 | 0.01 | 78.9942 | 16.4958 | 57.3647 | 11.9791 |
| 63.1941 | 16.2481 | 45.7074 | 11.7520 | |||||
| 55.1921 | 16.6459 | 39.9649 | 12.0534 | |||||
| 8 | 18 | 25 | 0.01 | 0.02 | 131.9280 | 36.2100 | 94.4705 | 25.9291 |
| 231.4801 | 35.7390 | 163.8349 | 25.2950 | |||||
| 163.5385 | 35.4443 | 119.0742 | 25.8074 | |||||
| 9 | 18 | 25 | 0.02 | 0.02 | 166.7012 | 35.5585 | 119.8884 | 25.5730 |
| 133.9105 | 33.4776 | 94.8299 | 23.7075 | |||||
| 162.0147 | 32.9827 | 113.8645 | 23.1804 | |||||
Для каждого варианта значений параметров было произведено несколько подходов по 1000 модельных просчетов. Имеем, что риск R2 является более устойчивым к изменению параметров, чем R1, так как является разностью средних величин.
При изменении ставок банковского депозита и ставки кредита на одну и туже величину риски меняются не пропорционально, т.е. при уменьшении ставки банковского депозита риск R2 уменьшается с 17 до 15.7. (1-3 варианты значений параметров.), при увеличении ставки кредита риск R2 увеличивается.
Если мы изменим, средние квадратические отклонения параметров: банковского депозита и ставки кредита на одну и ту же величину так же получим не пропорциональные изменения рисков, что говорит о разной степени влияния банковского депозита и ставки кредита.
Наибольшая степень влияния у ставки кредита, потому, что потоки проекта предполагают на ранней стадии значительные капитальные вложения, без какой-либо существенной отдачи от проекта – и за первые периоды наш долг значительно возрастает, потому что отдача от проекта идет на вложение в проект и обслуживание кредита. Проект окупается к восьмому периоду, и банковский депозит увеличивает прибыль от проекта не значительно.
Особенность данного типа проектов с большим числом периодов окупаемости в том, что при реализации проекта нужно следить за ставкой кредита.
Литература
- Наумов А.А., Шубин Д.А., Стрелюк И.В. Моделирование и оптимизация инвестиционных проектов.// Материалы VI Международной конференции АПЭП-2002, Т. 7. – Новосибирск: НГТУ, 2002, с. 65-67.
- Наумов А.А., Шубин Д.А., Стрелюк И.В. Оценивание рисков инвестиционных проектов на основе NFV-критерия.// Материалы конференции, Российская научно-методическая конференция с международным участием – Управление экономикой: Методы, модели, технологии. – Уфа: УГАТУ, 2002, с. 34-36.
- Шубин Д.А., Стрелюк И.В. Оценивание и анализ рисков инвестиционных проектов.// НАУКА. ТЕХНИКА. ИННОВАЦИИ // Региональная научная конференция студентов, спирантов и молодых ученых: Тез. докл. в 5-ти частях. Новосибирск: Изд-во НГТУ, 2002. Часть 3, с. 59-61.
- Шубин Д.А. Показатели эффективности инвестиционного проекта, основанные на NFV-подходе. Современные проблемы гуманитарных и социально-экономических наук: Сборник тезисов докладов Межвузовской научной студенческой конференции. Секция “Финансы”. – Новосибирск: НГАЭиУ, 2004, с. 26-27.