Применение теории нечетких множеств к задачам управления финансами
Журнал "Аудит и финансовый анализ"
1. АНАЛИЗ РИСКА ИНВЕСТИЦИЙ [18] 1.1. Описание проблемы и подход к ее разрешению Начнем наше изложение c двух базовых определений. Инвестиции - временный отказ экономического субъекта от потребления имеющихся в его распоряжении ресурсов (капитала) и использование этих ресурсов для увеличения в будущем своего благосостояния. Инвестиционный проект - план или программа мероприятий, связанных с осуществлением капитальных вложений с целью их последующего возмещения и получения прибыли. Инвестиционный процесс - развернутая во времени реализация инвестиционного проекта. Началом инвестиционного процесса является принятие решения об инвестициях, а концом - либо достижение всех поставленных целей, либо вынужденное прекращение осуществления проекта. Инвестиционный проект предполагает планирование во времени трех основных денежных потоков: потока инвестиций, потока текущих (операционных) платежей и потока поступлений. Ни поток текущих платежей, ни поток поступлений не могут быть спланированы вполне точно, поскольку нет и не может быть полной определенности относительно будущего состояния рынка. Цена и объемы реализуемой продукции, цены на сырье и материалы и прочие денежно-стоимостные параметры среды по факту их осуществления в будущем могут сильно разниться с предполагаемыми плановыми значениями, которые оцениваются с позиций сегодняшнего дня. Неустранимая информационная неопределенность влечет столь же неустранимый риск принятия инвестиционных решений. Всегда остается возможность того, что проект, признанный состоятельным, окажется de-facto убыточным, поскольку достигнутые в ходе инвестиционного процесса значения параметров отклонились от плановых, или же какие-либо факторы вообще не были учтены. Инвестор никогда не будет располагать всеобъемлющей оценкой риска, так как число разнообразий внешней среды всегда превышает управленческие возможности принимающего решения лица [19], и обязательно найдется слабоожидаемый сценарий развития событий (любая катастрофа, к примеру), который, будучи неучтен в проекте, тем не менее, может состояться и сорвать инвестиционный процесс. В то же время инвестор обязан прилагать усилия по повышению уровня своей осведомленности и пытаться измерять рискованность своих инвестиционных решений как на стадии разработки проекта, так и в ходе инвестиционного процесса. Если степень риска будет расти до недопустимых значений, а инвестор не будет об этом знать, то он обречен действовать вслепую. Способ оценки риска инвестиций прямо связан со способом описания информационной неопределенности в части исходных данных проекта. Если исходные параметры имеют вероятностное описание (например, см. [2, 3]), то показатели эффективности инвестиций также имеют вид случайных величин со своим импликативным вероятностным распределением (понятие импликативной вероятности см. в [
Альтернативный способ учета неопределенности - так называемый минимаксный подход. Формируется некий класс ожидаемых сценариев развития событий в инвестиционном процессе и из этого класса выбирается два сценария, при которых процесс достигает максимальной и минимальной эффективности соответственно. Затем ожидаемый эффект оценивается по формуле Гурвица [2, 3] с параметром согласия l . При l =0 (точка Вальда) за основу при принятии решения выбирается наиболее пессимистичная оценка эффективности проекта, когда в условиях реализации самого неблагоприятного из сценариев сделано все, чтобы снизить ожидаемые убытки. Такой подход, безусловно, минимизирует риск инвестора. Однако в условиях его использования большинство проектов, даже имеющих весьма приличные шансы на успех, будет забраковано. Возникает опасность паралича деловой активности, с деградацией инвестора как лица, принимающего решения.
Вот наглядный пример. Любой игрок в преферанс (даже такой захудалый, как я) знает, что в ходе торговли за прикуп игрок с высокой степенью повторяемости должен заявлять на одну-две взятки больше, чем у него есть на руках, в расчете на добрый прикуп. Иначе, по результатам множества игр он окажется в проигрыше или, в лучшем случае, “при своих”, потому что его соперники склонны к разумной агресии, т.е. к оправданному риску. Понимая инвестиции как разновидность деловой игры, мы скажем по аналогии: инвестору вменяется в обязанность рисковать, но рисковать рационально, присваивая каждому из потенциальных сценариев инвестиционного процесса свою степень ожидаемости. В противном случае он рискует потерпеть убыток от непринятия решения - убыток чрезмерной перестраховки. В карточной игре приличная карта, приличный прикуп приходят не так часто. В том же преферансе игрок, объявивший шесть взяток и сыгравший по факту восемь, вызывает всеобщее недовольство вероятным “перезакладом”. Становится обидно за партнера, за его неумение играть, когда по-настоящему приличная карта приходит так редко.
Инструментом, который позволяет измерять возможности (ожидания), является теория нечетких множеств. Впервые мы находим ее применение к инвестиционному анализу в [6]. Используя предложенный в этой работе подход, построим метод оценки инвестиционного риска, как на стадии проекта, так и в ходе инвестиционного процесса.
1.2. Описание метода анализа эффективности инвестиций в нечеткой постановке
В литературе по инвестиционному анализу (например, в [20, 21, 22]) хорошо известна формула чистой современной ценности инвестиций (NPV - Net Present Value). Возьмем один важный частный случай оценки NPV, который и будем использовать в дальнейшем рассмотрении:
1. Все инвестиционные поступления приходятся на начало инвестиционного процесса.
2. Оценка ликвидационной стоимости проекта производится post factum, по истечении срока жизни проекта.
Тогда соотношение для NPV имеет следующий вид:
![]() , ( 17)
, ( 17)
где
I - стартовый объем инвестиций,
N - число плановых интервалов (периодов) инвестиционного процесса, соответствующих сроку жизни проекта,
D Vi - оборотное сальдо поступлений и платежей в i-ом периоде,
ri - ставка дисконтирования, выбранная для i-го периода с учетом оценок ожидаемой стоимости используемого в проекте капитала (например, ожидаемая ставка по долгосрочным кредитам),
C - ликвидационная стоимость чистых активов, сложившаяся в ходе инвестиционного процесса (в том числе остаточная стоимость основных средств на балансе предприятия).
Инвестиционный проект признается эффективным, когда NPV, оцененная по (17), больше определенного проектного уровня G (в самом распространенном случае G = 0).
Замечания.
1. NPV оценивается по формуле (17) в постоянных (реальных) ценах.
2. Ставка дисконтирования планируется такой, что период начислений процентов на привлеченный капитал совпадает с соответствующим периодом инвестиционного процесса.
3. (N+1
)-й интервал не относится к сроку жизни проекта, а выделен в модели для фиксации момента завершения денежных взаиморасчетов всех сторон в инвестиционном процессе (инвесторов, кредиторов и дебиторов) по кредитам, депозитам, дивидендам и т.д., когда итоговый финансовый результат проекта сделается однозначным.Если все параметры в (17) обладают “размытостью”, т.е. их точное планируемое значение неизвестно, тогда в качестве исходных данных уместно использовать так называемые треугольные нечеткие числа с функцией принадлежности следующего вида (рис. 3).

Рис. 3. Функция принадлежности треугольного нечеткого числа
АЭти числа моделируют высказывание следующего вида: “параметр А приблизительно равен ![]() и однозначно находится в диапазоне [amin, amax]”.
и однозначно находится в диапазоне [amin, amax]”.
В общем случае под нечетким числом понимается нечеткое подмножество универсального множества действительных чисел, имеющее нормальную и выпуклую функцию принадлежности [6]. Такое описание позволяет разработчику инвестиционного проекта взять в качестве исходной информации интервал параметра
[amin, amax] и наиболее ожидаемое значениеТеперь мы можем задаться следующим набором нечетких чисел для анализа эффективности проекта:
![]() - инвестор не может точно оценить, каким объемом инвестиционных ресурсов он будет располагать на момент принятия решения;
- инвестор не может точно оценить, каким объемом инвестиционных ресурсов он будет располагать на момент принятия решения;
![]() - инвестор не может точно оценить стоимость капитала, используемого в проекте (например, соотношение собственных и заемных средств, а также процент по долгосрочным кредитам);
- инвестор не может точно оценить стоимость капитала, используемого в проекте (например, соотношение собственных и заемных средств, а также процент по долгосрочным кредитам);
![]() - инвестор прогнозирует диапазон изменения денежных результатов реализации проекта с учетом возможных колебаний цен на реализуемую продукцию, стоимости потребляемых ресурсов, условий налогообложения, влияния других факторов;
- инвестор прогнозирует диапазон изменения денежных результатов реализации проекта с учетом возможных колебаний цен на реализуемую продукцию, стоимости потребляемых ресурсов, условий налогообложения, влияния других факторов;
![]() - инвестор нечетко представляет себе потенциальные условия будущей продажи действующего бизнеса или его ликвидации;
- инвестор нечетко представляет себе потенциальные условия будущей продажи действующего бизнеса или его ликвидации;
![]() - инвестор нечетко представляет себе критерий, по которому проект может быть признан эффективным, или не до конца отдает себе отчет в том, что можно будет понимать под “эффективностью” на момент завершения инвестиционного процесса.
- инвестор нечетко представляет себе критерий, по которому проект может быть признан эффективным, или не до конца отдает себе отчет в том, что можно будет понимать под “эффективностью” на момент завершения инвестиционного процесса.
Замечания.
1. В том случае, если какой-либо из параметров
2. В отношении вида
Таким образом, задача инвестиционного выбора в приведенной выше постановке есть процесс принятия решения в расплывчатых условиях, когда решение достигается слиянием целей и ограничений [24].
Чтобы преобразовать формулу (17) к виду, пригодному для использования нечетких исходных данных, воспользуемся сегментным способом, как это сделано в [6].
Зададимся фиксированным уровнем принадлежности a (см. рис. 3) и определим соответствующие ему интервалы достоверности по двум нечетким числам
[a1, a2] (+) [b1, b2] = [a1 + b1, a2 + b2], ( 18)
- операция “вычитания”:
[a1, a2] (-) [b1, b2] = [a1 - b2, a2 - b1], ( 19)
- операция “умножения”:
[a1, a2] (´ ) [b1, b2] = [a1 ´ b1, a2 ´ b2], ( 20)
- операция “деления”:
[a1, a2] (/) [b1, b2] = [a1 / b2, a2 / b1], ( 21)
- операция “возведения в степень”:
[a1, a2] (^) i = [a1i , a2i]. ( 22)
По каждому нечеткому числу в структуре исходных данных получаем интервалы достоверности
[I1, I2], [ri1, ri2], [D Vi1, D Vi2], [C1, C2]. И тогда, для заданного уровня a , путем подстановки соответствующих границ интервалов в (1) по правилам (18) - (22), получаем:![]()
![]()
![]()
![]()
![]() ( 23)
( 23)
Задавшись приемлемым уровнем дискретизации по a на интервале принадлежности [0, 1], мы можем реконструировать результирующее нечеткое число
Часто оказывается возможным привести
Перейдем к оценке собственно риска инвестиций. На рис. 4 представлены функции принадлежности ![]() и критериального значения
и критериального значения ![]() .
.

Рис. 4. Функции принадлежности
NPV и GТочкой пересечения этих двух функций принадлежности является точка с ординатой
a 1. Выберем произвольный уровень принадлежности a и определим соответствующие интервалы [NPV1, NPV2] и [G1, G2]. При a > a 1 NPV1 > G2, интервалы не пересекаются, и уверенность в том, что проект эффективен, стопроцентная, поэтому степень риска неэффективности инвестиций равна нулю. Уровень a 1 уместно назвать верхней границей зоны риска. При 0 £ a £ a 1 интервалы пересекаются. На рис. 5 показана заштрихованная зона неэффективных инвестиций, ограниченная прямыми G = G1, G = G2, NPV = NPV1, NPV = NPV2 и биссектрисой координатного угла G = NPV.
Рис. 5. Фазовое пространство
(NPN, G)Взаимные соотношения параметров
G1,2 и NPV1,2 дают следующий расчет для площади заштрихованной плоской фигуры: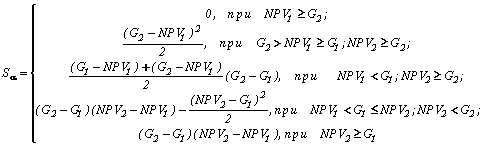 ( 24)
( 24)
Поскольку все реализации
(NPV, G) при заданном уровне принадлежности a равновозможны, то степень риска неэффективности проекта j (a ) есть геометрическая вероятность события попадания точки (NPV, G) в зону неэффективных инвестиций:![]() , ( 25)
, ( 25)
где
Sa оценивается по (24).Тогда итоговое значение степени риска неэффективности проекта:
![]() ( 26)
( 26)
В важном частном случае (см. рис. 6), когда ограничение
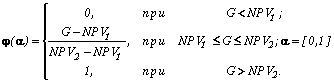
( 27)
Для того чтобы собрать все необходимые исходные данные для оценки риска, нам потребуется два значения обратной функции m
NPV-1(a 1). Первое значение есть G (по определению верхней границы зоны риска a 1), второе значение обозначим G'. Аналогичным образом обозначим NPVmin и NPVmax - два значения обратной функции m NPV-1(0).
Рис. 6. Пример четкого критерия эффективности
Также введем обозначение
 ( 28)
( 28)
где
 ( 29)
( 29)

( 30)
Исследуем выражение (28) для трех частных случаев:
1. При
G = NPVmin (предельно низкий риск) R = 0, a 1 = 0, G' = NPVmax, и предельный переход в (28) дает V&M = 0.2. При
G = G' =3. При
G = NPVmax (предельно высокий риск) P = 0, a 1 = 0, G' = 0, и предельный переход в (28) дает V&M = 1.Таким образом, степень риска
V&M принимает значения от 0 до 1. Каждый инвестор, исходя из своих инвестиционных предпочтений, может классифицировать значения V&M, выделив для себя отрезок неприемлемых значений риска. Возможна также более подробная градация степеней риска. Например, если ввести лингвистическую переменную “Степень риска” со своим терм-множеством значений {Незначительная, Низкая, Средняя, Относительно высокая, Неприемлемая}, то каждый инвестор может произвести самостоятельное описание соответствующих нечетких подмножеств, задав пять функций принадлежности m * (V&M).Описание метода анализа эффективности инвестиций в нечеткой постановке с оценкой степени риска ошибки инвестиционного решения - завершено. Рассмотрим простой пояснительный пример.
1.3. Пример анализа риска
Исходные данные проекта:
N = 2,Результаты расчетов по формуле (23) для уровней принадлежности a
= [0, 1] с шагом 0.25 сведены в табл. 12.Аппроксимация функции m
NPV (рис. 7) показывает ее близость к треугольному виду: ( 31)
( 31)
Этим видом мы будем пользоваться в расчетах.
Таблица 12
РАСЧЕТЫ ИНТЕРВАЛОВ ДОСТОВЕРНОСТИ
|
a |
Интервалы достоверности по уровню принадлежности a для: |
||
|
r |
D V |
NPV |
|
|
1 |
[0.2, 0.2] |
[1, 1] |
[0.527, 0.527] |
|
0.75 |
[0.175, 0.225] |
[0.75, 1.25] |
[0.112, 1.068] |
|
0.5 |
[0.15, 0.25] |
[0.5, 1.5] |
[-0.280, 1.438] |
|
0.25 |
[0.125, 0.275] |
[0.25, 1.75] |
[-0.650, 1.944] |
|
0 |
[0.1, 0.3] |
[0, 2] |
[-1, 2.470] |

Рис. 7. Приведение
NPV к треугольному видуПусть принято положительное решение об инвестировании капитала ![]() . Тогда a
1 = m
NPV(0) = 0.655, G' = m
NPV-1(a
1) = 1.197 и, согласно (28) - (31), R = =0.288, V&M = 0.127.
. Тогда a
1 = m
NPV(0) = 0.655, G' = m
NPV-1(a
1) = 1.197 и, согласно (28) - (31), R = =0.288, V&M = 0.127.
2.4. Коррекция оценки риска в ходе инвестиционного процесса
Продолжим рассмотрение расчетного примера. Пусть принято решение о начале инвестиционного процесса, и по результатам первого периода зафиксировано оборотное сальдо
D V1 = 1 при фактически измеренной ставке дисконтирования r1 = 0.2. Тогда перерасчет интервальной оценки NPV по (23) дает:![]() ( 32)
( 32)
Результаты расчетов по формуле (32) сведены в табл. 13.
Приведение
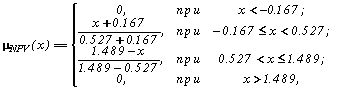 ( 33)
( 33)
откуда
a 1 = m NPV(0) = 0.241, G' = m NPV-1(a 1) = 1.257, и, согласно (28) - (30), R = 0.101, V&M = 0.013.Таблица 13
РАСЧЕТЫ ИНТЕРВАЛОВ ДОСТОВЕРНОСТИ ДЛЯ СЛУЧАЯ КОРРЕКЦИИ ОЦЕНКИ РИСКА
|
a |
Интервалы достоверности по уровню принадлежности a для: |
||
|
r |
D V |
NPV |
|
|
1 |
[0.2, 0.2] |
[1, 1] |
[0.527, 0.527] |
|
0.75 |
[0.175, 0.225] |
[0.75, 1.25] |
[0.333, 0.738] |
|
0.5 |
[0.15, 0.25] |
[0.5, 1.5] |
[0.153, 0.967] |
|
0.25 |
[0.125, 0.275] |
[0.25, 1.75] |
[-0.012, 1.227] |
|
0 |
[0.1, 0.3] |
[0, 2] |
[-0.167, 1.489] |
Видим, что за счет снижения уровня неопределенности степень риска понизилась почти на порядок. Таким образом, у инвестора появляется эффективный инструмент контроля эффективности инвестиционного процесса.
2.5. Измерение уровня информационной неопределенности
Из расчетов видно, что чем значительнее неопределенность в исходных данных, тем выше риск. Поэтому в ряде случаев инвестор просто обязан отказаться от принятия решения и предпринять дополнительные меры по борьбе с неопределеннностью. Чтобы знать, когда оправдан отказ от принятия решения, инвестору необходим измеритель неопределенности сложившейся информационной ситуации (неустойчивости проекта [2, 3]). Логично производить такие измерения по показателю
a 1. Для случая полной определенности a 1=0. Применительно к m NPV(x) вида (31) расчеты дают a 11 = 0.655, а для m NPV(x) вида (33) a 12 = 0.241 < a 11 . Инвестор опять же может интерпретировать значения a 1 лингвистически, как и в случае лингвистической оценки степени риска, и таким образом обозначить для себя границу a 1, за которой неопределенность перестает быть приемлемой.2.6. Развитие предложенного подхода
В качестве дополнительного критерия эффективности инвестиций инвестор может потребовать, чтобы уровень внутренней ставки доходности (IRR - Internal Rate of Return) проекта превышал некий нечеткий порог
Строгий с математической точки зрения подход к использованию показателя
IRR в инвестиционном анализе см. в [25].Выводы
Нечеткие множества - это инструмент расчета возможностей [5]. Умея грамотно описать нечеткость исходных данных, мы логическим путем переходим к нечеткости результирующих показателей. Оценка инвестиционного риска - это оценка меры возможности неблагоприятных событий в ходе инвестиционного процесса, когда ожидаемость таких событий, задаваемая функцией принадлежности соответствующих нечетких чисел, известна или определяется специальными методами.
Подход, основанный на нечеткостях, преодолевает недостатки вероятностного и минимаксного подходов, связанные с учетом неопределенности. Во-первых, здесь формируется полный спектр возможных сценариев инвестиционного процесса. Во-вторых, решение принимается не на основе двух оценок эффективности проекта, а по всей совокупности оценок. В-третьих, ожидаемая эффективность проекта не является точечным показателем, а представляет собой поле интервальных значений со своим распределением ожиданий, характеризующимся функцией принадлежности соответствующего нечеткого числа. А взвешенная полная совокупность ожиданий позволяет оценить интегральную меру ожидания негативных результатов инвестиционного процесса, т.е. степень инвестиционного риска.
Метод, названный нами V&M-метод оценки риска инвестицийÓ , и предложенный здесь показатель степени риска, названный нами V&M-показатель оценки риска инвестицийÓ , использованы в разработанной консультационной группой “Воронов и Максимов” программной модели “МАСТЕР ПРОЕКТОВ: Предварительная оценка” и широко применяются в автоматизированном инвестиционном анализе.