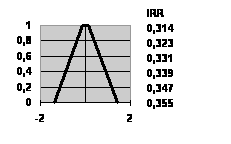Нечеткое составление бизнес-плана: оценка инвестиционного проекта, оптимизация.

Резюме

Составление бюджета основано на анализе некоторых финансовых параметров рассматриваемых инвестиционных проектов. Ясно, что оценка инвестиционной эффективности, так же как любой прогноз, является довольно неточной. В случае инвестиционного проекта мы можем предсказать до некоторой степени будущую прибыль, используя историю предыдущего периода и статистический метод, но только для маленького горизонта времени. В реальных активных инвестициях мы обычно имеем дело с бизнес-планом, который реализуется, как правило несколько лет. В таких случаях, описание неопределенности в пределах структуры традиционных методов вероятности обычно невозможно из-за отсутствия объективной информации о будущих вероятностях событий. Именно поэтому, в течение прошлых двух десятилетий возрос интерес к применению интервальных нечетких методов в составлении бюджета имеет быть. В данной статье нечеткостью - представлена оценка интервала финансовых параметров. Это позволяет использовать с большей точностью чем традиционные методы априорно неуверенную информацию о будущих потоках наличности, процентных ставках. Как результат возможность получать нечеткий интервал и вес не нечеткого значения для главных финансовых параметров NPV и IRR, так же как количественная оценка риска инвестиций.

Другая проблема состоит в том, что обычно мы должны счесть ряд различных местных критериев основанным на финансовых параметрах инвестиций. Как одно из возможного решения, числовой метод для оптимизации будущих потоков наличности в нечеткой постановке, рассматривая качественный критерий обобщенного проекта как компромисс между частными критериями максимизации прибыли и  минимизация финансового риска.

1.    Введение

Сначала, рассмотрим обычные не нечеткие подходы к  составлению бюджета, планируемого проекта. Есть много финансовых параметров, предложенных в литературе  для составления бюджета.

Основные из них: Чистая Приведенная Стоимость (NPV), Внутренняя Норма Возвращаемости (IRR), период Окупаемости (PB), Индекс Доходности (PI). Эти параметры обычно используются для проектной количественной оценки, но практически они имеют огромное значение.

Отсюда видно, что самые важные параметры - NPV и IRR (см. Таблицу. 1).

Поэтому, наше дальнейшее рассмотрение будет основано на анализе только NPV и IRR. Хороший обзор других полезных финансовых параметров находится в [6].

Таблица 1. Частота финансового использования параметров (от 103 наибольших нефтяных и газовых компаний США в 1983)

Тип использования

Чистая Приведенная Стоимость обычно вычисляется следующим образом:

 ,         (1)

где d - учетная ставка; t_n - стартовый год; t_c - год окончания инвестиций; KV_t - капиталовложение в t году,  P_t-  является доходом в t году, T - продолжительность инвестиционного проекта в годах.

Обычно учетная ставка равна средней норме банковского процента в стране инвестора или равна другой соответствующему значению для оценки возвращения в случае альтернативных капиталовложений в другие проекты или ценные бумаги.

Экономический характер внутренней нормы возвращения ( IRR) можно объяснить следующим образом. Как альтернатива инвестициям, пример: планируют внесения под некоторый банковский процент (распределенный во  времени как в случае проектного анализа). Предложено, что все доходы, которые будут получены в течение реализации проекта, будут также депонированы с той же самой процентной ставкой. Если учетная ставка - равна IRR, то инвестиции в проекте дадут минимальные выгоды, равные начальным вложениям. Таким образом, обе альтернативы экономически эквивалентны. Если фактическая норма банковской учетной ставки - менее IRR данного проекта, инвестиции в проект более предпочтительны. Поэтому IRR - пороговая учетная ставка, выбирающая эффективный и неэффективные инвестиционные проекты. Значение IRR - решение нелинейного уравнения относительно d:

                                               (2)

Оценка IRR часто используется как первый шаг финансового анализа. Только проекты с IRR, которое не ниже чем некоторое принятое пороговое значение (обычно 15-20 %) выбирают для дальнейшего рассмотрения.

В настоящее время, традиционный подход к оценке NPV, IRR и других финансовых параметров подвергнут весьма заслуженной критике, начиная с будущих P_t,  доходов, капиталовложения_, KV_t и нормы d являются довольно сомнительными параметрами. Сомнения, которые мы встречаем в составлении бюджета капитала, отличаются от тех, которые существуют в случае прогноза цен акции и не могут быть соответственно описаны в терминах вероятности. В реальных активных инвестициях мы обычно имеем дело с бизнес-планом, который реализуется долгое время как правило несколько лет. В таких случаях, описание неопределенности в пределах структуры традиционных методов вероятности обычно невозможно из-за отсутствия объективной информации о будущих вероятностях событий. Таким образом, что мы действительно имеем в таких случаях, - оценки некоторого эксперта. В реальных мировых ситуациях, инвесторы или вовлеченные эксперты в состоянии предсказать уверенно только интервалы возможного  значения Pt,, KVt и d и наиболее ожидаемых значений в этих интервалах. Именно поэтому, в течение прошлых двух десятилетий рос интерес к применению интервальной арифметики [7] и методов нечеткой теории множеств [8].

После работ T.L.Ward [9] и J.U. Buckley [10], некоторые другие авторы внесли свой вклад в развитие нечеткого составления бюджета, планирующими теориями [11-24]. Мы можем теперь сказать, когда почти все проблемы нечеткой оценки NPV решены, но интересная и важная проблема оценки риска проекта на основе нечеткого NPV становится первым приоритетом.

Нерешенная проблема - нечеткая оценка IRR.  [9] рассматривая (2) и объясняется, что такое выражение не может использоваться для нечеткого случая потому что правая сторона  уравнения (2) нечеткая, а 0 является четким, и равенство невозможно. Следовательно, выражение (2) является бессмысленным в нечеткой постановке.

В [22] предложен метод для нечеткой оценки IRR, где a -сокращенное представление нечетких чисел [25]. Этот метод, при условии [ [22] стр. 380] устанавливает из уравнений для определения IRR на каждом a-уровне, может быть представлен как (в нашем примечании)

,                                   (3)

где , i=0 до n, являются четким представлениями интервала нечетких потоков наличности на a-уровнях. Конечно, из линейных уравнений (3) могут быть получены все четкие интервалы , выражающие значения нечеткого IRR. Прискорбной, есть небольшая ошибка в (3). В правой части представление интервала выражения (2) на  a -уровнях должно быть написано: 

.                                    (4)

Нет никакого способа получить решения для IRR ^a из выражения (4), но реально это значение можно получить (см. раздел 3, ниже).

Другая проблема, не рассмотренная в литературе - оптимизация потоков наличности в нечеткой постановке.

Остальная часть статьи изложена следующим образом. В разделе 2 мы вспоминаем метод для нечеткой оценки NPV и вводим оценку риска, основанную на концепции степени нечеткости. Раздел 3 описывает метод текущего значения, решая выражение (2) в случае нечетких потоков наличности. Предложены и проанализированы также набор полезных реальных значений параметров объединенных с реальным решением значения уравнения (2) также. В разделе 4, предложен числовой метод для оптимизации потоков наличности как компромисс между конкретными критериями максимизации прибыли и минимизации финансового риска.

2.    Нечеткий NPV и оценка риска связанная с ним.

Предлагаемая техника основана на нечетком расширенном принципе [8]. Таким образом, значениями сомнительной  P_t, KV_t и d параметров, заменяют, нечеткими интервалами. Практически это означает, что нижний опытный набор - P_t1 (пессимистическое значение) и верхний - P_t4 (оптимистическое значение) границы интервалов и внутренних интервалов наиболее ожидаемых значений [P_t2, P_t3]  для анализа параметров (см. рис. 1). m( P_t) функции обычно интерпретируется как функция принадлежности, то есть степень, к которой значение параметра принадлежат определенному интервалу (в нашем случае [ P_t1, P_t4]). Функция принадлежности изменяется непрерывно от 0 (область из интервала) до максимального значения, равного 1, в области наиболее возможных значений. Очевидно, что функция принадлежности является обобщением характеристической функции обычного множества, которая равна 1 если все значения параметров принадлежат множеству, и равна 0 во всех других случаях.

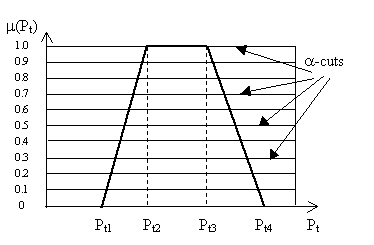
Рисунок 1.  Нечеткий интервал нечеткого параметра P_t  и его функция принадлежности m( P_t ).

Линейный характер функции не обязателен, но такой способ - наиболее используемый и позволяет представлять нечеткие интервалы -  в удобной форме учетверенной P_t = { P_t1, P_t2, P_t3, P_t4}. Тогда все необходимые вычисления выполнены, используя специальное нечеткое - правила интервальной арифметики.

Позвольте нам напомнить некоторые основные принципы нечеткой арифметики [25].

Вообще, для произвольных форм функций принадлежности техника нечеткого - вычисления интервала основана на представлении начальных нечетких интервалов так называемыми   a--отрезками (Рис. 1), которые, фактически, четкие интервалы, связанные с соответствующими степенями принадлежности. Все дальнейшие вычисления сделаны с этими   a-отрезками соответственно с известными четкими арифметическими интервалами и нечеткими – интервалами, полученными как дизъюнкция соответствующих  вычисляемых a-отрезков.

Таким образом, если f (A) - нечеткое число, то

Где A _a    - четкий интервал {x: m_A (x) ³ a }, a A _a   - нечеткий интервал {( x, a): x Î A _a  }. Таким образом, если A, B, Z - нечеткие числа (интервалы), и @- операция  {+,-, *,/} тогда

Z = À@Â=.                                                      (5)

С тех пор в случае a-сокращенного представления, нечеткая арифметика основана на четких правилах интервальной арифметики, основные определения прикладного интервального анализа также должны быть представлены. Есть некоторые определения интервальной арифметики (см. [26,27]), но в практических применениях обычно используется так называемая "простая" форма. Согласно этому, если А = [a₁, a₂] и В = [b₁, b₂] - четкие интервалы, то

Z = А@В={ z=x@y,  }.                                           (6)

Как прямое следствие основного выражения (6) были получены следующие выражения: 

А +В=[a ₁+ b₁ , b ₂+ b₂ ],       А-В =[a ₁- b₂ , a ₂- b₁ ],

А·В=[min(a₁·b₁, a₂· b₂, a₁·b₂, a₂·b₁), max(a₁·b₁, a₂· b₂, a₁·b₂, a₂·b₁)],          

А/В=[ a₁, a₂] · [1/ b₂, 1/b₁]

Конечно, есть много внутренних проблем в пределах прикладного интервального анализа, как случай, нолевой интервал, но вообще этот метод можно рассматривать как хороший математический инструмент для того, чтобы производить моделирование в условиях неопределенности. 

Проиллюстрируем это, рассматривая пример. Предположим есть инвестиционный проект, реалтизация которого происходит в течении двух лет с инвестициями KV₀и KV₁соответственно. Прибыль ожидается только после окончания фазы здания и будет получена в течение двух лет (_P2 и _P3). Предположено, что нечеткий интервал для ставки d остается устойчивым в течение времени проектной реализации. Соответствующие трапециевидные начальные нечеткие интервалы будут следующие: KV₀ = {2,2.8,3.5,4}; KV₁ = {0,0.88,1.50,2}; KV₂ = {0,0,0,0}; KV₃ = {0,0,0,0}; P₀ = {0,0,0,0}; P₁ = {0,0,0,0}; P₂ = {6.5 7.5 8.0 8.5}; P₃ = {5.5 6.5 7.0 7.5}; d = {0.08,0.13,0.22,0.35}.

Получающийся нечеткий интервал NPV, вычислим используя нечеткое выражение (1), представлен в рис. 2.

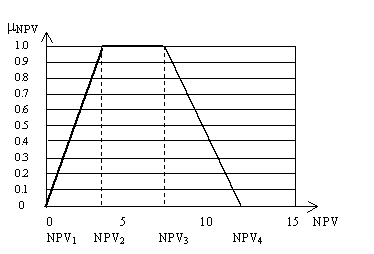
Рисунок 2. Результирующий нечеткий интервал  NPV.

Полученный нечеткий интервал позволяет оценивать границы возможных значений планируемого NPV, интервал наиболее ожидаемых значений, и также что является очень важным,  дает оценку степени финансового риска инвестиций.

Чтобы оценить финансовый риск, мы приним во внимание следующую особенность нечетких множеств. Предположим  есть некоторое нечеткое подмножество X, описываемое функцией принадлежности m(A). Тогда дополнительное нечеткое подмножество `A  имеет функцию принадлежности m( `A)=1- m(A). Основное различие, нечеткого подмножества от обычных точных - то, что пересечение нечеткого A и ` A  не пусто, а A Ç `A= B, где B – непустое  нечеткое подмножество. Ясно, что  чем ближе А к ` A, тем больше множество B и больше A.

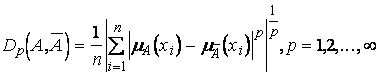                                 (7)

 Следовательно, тип нечеткости может быть определен как 

                                                                                 (8)

Определение (8) находится в согласии с очевидными запросами к типу нечеткости. Если A - нечеткое подмножество  X, m(A)  - его функция членства, и dd - соответствующий тип нечеткости, то после должно соблюдаться:

1)  dd (A) = 0, если A - четкое подмножество;

2)  dd (A) имеет максимальное значение если if  m( A) = 1/2 для x ÎX;

3) style='font:7.0pt "Times New Roman"'>      dd (А1)> dd (A), если   m (х)< m (y)  (x Î A1; y Î A).

Доказано, что введенная мера подобна Шеннонской мере энтропии [28].

 В самом полезном случае (p = 1) выражение (8) преобразовано к

    .                                                                                (9) 

Ясно (см. выражение (9)), что уровень нечеткости повышается от 0, если m(A) = 1 (четкое подмножество), до 1, если m(A) = 1/2  (максимальная степень нечеткости).

 Относительно нашей проблемы степени не нечеткости нечеткого интервала NPV может лингвистически интерпретироваться как риск или неуверенность в получении Чистой Приведенной стоимости в интервале [ NPV₁, NPV₄]. Действительно, чем более точный, (более "прямоугольный") интервал, который мы получаем, тем больше степени неопределенности и риска мы получаем. Конечно, сначала это утверждение кажется парадоксальным. Однако, любой точный интервал не содержит никакой дополнительной информации об относительном предпочтении значений, помещенных в нем. Поэтому, он содержит менее полезную информацию, чем любой нечеткий интервал, построенный на его основании. В последнем случае дополнительная информация, для сокращение неопределенности получена из функции принадлежности выбранного нечеткого интервала.

Таким образом, подход, предложенный для оценки  NPV основан на двух критериях для оценки будущей прибыли: нечетком интервале NPV и степени его неопределенности (степени риска).  

Поэтому, проблема оценка эффективности инвестиций на основе NPV, основанная на двух критериях,  требует специального подхода и соответствующей техники. Недавно, мы предложили, чтобы такая техника [29] основывалась на нечеткой теории множеств, однако ее детальное рассмотрение - вне возможностей этой статьи.

3.    Набор реальной значений оценки IRR, основанные на нечетких потоках наличности

В основном, проблема внутренней процентной ставки (IRR)  выглядит как нечеткое решение для интервала (2) относительно d.

Доказано, что решение уравнений с нечеткими параметрами возможно по выражению этих параметров (( P_t , KV_t и d в нашем случае) как множества  a- отрезков. Как результат для проблемы оценки IRR мы получаем систему нелинейных интервальных четких - уравнений:

,                                                        (10)

где [[ P_t] _a , [KV_t] _a и [ d] четкие интервалы при  a-уровнях.

Вообще, мы можем заявить что простое предположение в правой части выражения (10) - нулевой интервал [0,0], не гарантирует получение адекватных результатов,  ненулевой интервал слева (10), позволяют нам рассматривать эту ситуацию полностью.    

Как самый простой пример, рассмотрим двухлетний проект, когда все инвестиции закончены на первом году, и производство и получение доходов начинаются и заканчиваются на втором году. Тогда каждое из уравнений для a-уровней (10) должно быть разделено на два

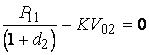 - левая граница интервала NPV

     (11)

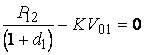   - правая граница интервала NPV

Формальное решение (10) относительно d₁ и d₂ тривиально:

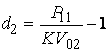, однако это бессмысленно, поскольку получается правая граница интервала [d1, d2] всегда меньше чем левая.

Этот, на первый взгляд, абсурдный результат можно легко объяснить с помощью общих методологических положений. Действительно, правила интервальной математики построены так, что любые арифметические операции с интервалами дают нам интервал. Эти правила находятся в полном соответствии известному общему методическому положению, согласно которому любая арифметическая операция с нечеткостями, увеличивает полную неопределенность и энтропию системы. Поэтому, если в нашем случае мы поместим в правой стороне (10) и (11) нулевые интервалы, то это будет эквивалентно запросу сокращения неопределенности в левых частях до ноля, что возможно только в случае обратного знака интервала [d₁, d₂], что в свою очередь можем интерпретировать как отрицательная энтропия системы.

Таким образом, присутствие нулевого интервала в правых сторонах уравнений неправильно. Более приемлемый подход к решению этой проблемы был построен с помощью следующих принципов. Легко видеть, анализируя выражения (11), что при любом значение d₁ минимальная ширина интервала NPV достигается если d₂ = d₁. В соответствии с общими методическими положениями: минимальная неопределенность в результате (NPV) достигается в случае минимальной неопределенности в используемых параметрах всей системы. Ясно (см. рис. 3), что самое разумное решение "нулевой" проблемы - выбор середины интервала NPV, которая будет помещена в нулевую точку (требование симметрии интервала относительно  ноля).

Очевидное, на первый взгляд, намерение минимизировать размеры полученного интервала, NPV приводит к получению положительных или отрицательных интервалов минимальной ширины, но не пересечения нулевой точки, который не соответствует естественному определению ноля, содержащего интервал. Помимо этого может быть легко доказан, что только запрос симметрии ноля, содержащего интервал гарантирует асимптотически действительный результат в случае сокращения границ всех продуманных интервалов к их центрам.

Таким образом, вообще проблема сокращена до поиска такого точного d значения(неинтервала), которое может обеспечить симметрию относительно ноля получающиеся интервалы NPV на каждом a-сокращенный в уравнениях (10), то есть гарантировало бы выполнение требование ( NPV₁ + NPV₂) = 0, для каждого a = 0 0.1 0.2 ..., 1.

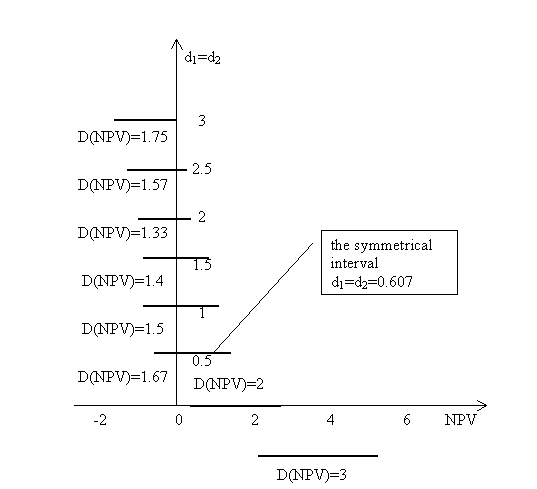
Рисунок 3. Дисконтная зависимость интервала NPV, когда инвестиции на первом году - KV0 = [1,2]], доход на втором году, P1 = [2,3]: и D (NPV) - ширина интервала NPV.

Чтобы проиллюстрировать вышеупомянутые теоретические рассмотрения, давайте сравнивать два инвестиционных проекта, которые должны быть реализованы в течение 4 лет. Нечеткие потоки наличности   K_t = P_t- KV_t  определены с помощью формы с четырьмя контрольными точками, описанными выше (см. Таблицу 2). Цена, отмечает, что данные первого проекта более точные.

Таблица 2. Нечеткие параметры сравниваемых проектов.

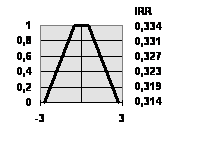
Результаты оценок для двух сравнивающихся инвестиционных проектов с различными нечеткими потоками наличности представлены на рис. 4. Замечено, что значение IRR _a, полученного для каждого a-уровня могут увеличиться или уменьшиться с ростом a и был получен результат для каждого проектного собственного множества возможных реальных значений числа IRR . Таким образом, появилась проблема интерпретации результатов.   

Для этого, мы предлагаем уменьшить множества IRR _a, полученного на каждом отрезке a-к небольшому множеству параметров, которые могут легко интерпретироваться. Первый элементарный параметр - среднее значение оценивает IRR_m  - является конечно удобным, однако не принимает во внимание, что с ростом a надежность результата увеличивается также, то есть. IRR _a,, полученные на более высоких a-отрезках более ожидаемые, чем полученный на более низких, из определения a-отрезка. С другой стороны, точные интервалы [NPV1, NPV2] _a, соответствующий каждому из IRR _a  имеет ширину, которая является мерой неопределенности для полученного не интервала оцениваемого IRR _a, начиная с ширины интервалов [ NPV1, NPV2] _a характеризуют количественно различие левой части (10) от нулевого интервала [0,0]. Это позволяет нам вводить две взвешенных оценки IRR на множестве IRR _a  наименее ожидаемый (наименее надежный) )  IRR_min и наиболее ожидаемый (самый надежный) IRR_max   :

,                                                      (12)

,                                                                              (13)

 где n - число a-отрезков.

В практике принятия решения, выбирая лучший проект, достаточно использовать все три предложенных параметра IRR_m, IRR_min, IRR_max.

Интерпретация [NPV1, NPV2] _a, поскольку выполнение для неопределенности IRR_a позволяет предлагать количественное и выраженный в денежно-кредитных оценках единиц финансового риска проекта, который рассматривает (степень неопределенности полученных значений IRR_ср, IRR_min, IRR_max как следствие начальной неопределенности данных):

                           (14)

Параметр R_m может играть ключевую роль для оценки эффективности проекта.

Для нашего примера:

Проект 1:            IRR_min = 0,34;  IRR_max = 0,327; IRR_ср = 0,335; R_ср = 1,56.    

Проект 2:            IRR_min = 0,322; IRR_max = 0,329; IRR_ср = 0,325; R_ср = 3,52.

Таким образом, рассмотренные проекты имеют довольно близкие значения IRR_ср, IRR_min, IRR_max. В то же самое время, значение риска R_cp для второго проекта значительно выше чем риск первого. Так, первый проект - лучший.

 Кроме параметров, описанных выше, есть некоторые другие полезные оценки: IRR_nr - самое надежное значение IRR_a - связанное с минимальным интервалом [ NPV1, NPV2] _nr среди всех [ NPV1, NPV2] _a и IRR _nr - наименее надежное значение IRR_a - связанный с максимальным интервалом [NPV1, NPV2] _r  среди всего [NPV1, NPV2] _a. Видно, что [NPV1, NPV2] _nr и [NPV1, NPV2] _r - оценки риска для соответствующего IRR_nr и IRR_r.