Neural Information Processing - Letters and Reviews
Vol. 10, Nos. 8-9, Aug.-Sept. 2006
LETTER
Ultrasound Image Segmentation by Using Wavelet Transform and SelfOrganizing Neural Network
Zafer Iscan, Mehmet Nadir Kurnaz, Zumray Dokur, and Tamer Olmez
Department of Electronics and Communication Engineering Istanbul Technical University, 34469 Istanbul, Turkey
E-mail: zafer@ehb.itu.edu.tr
(Submitted on April 21 and July 7, 2006; Accepted on August 8, 2006)
Abstract - This paper presents an improved incremental self-organizing map (I2SOM) network that uses automatic threshold (AT) value for the segmentation of ultrasound (US) images. In order to show the validity of proposed scheme, it has been compared with Kohonen’s SOM. Two-dimensional (2D) fast Fourier transform (FFT) and 2D continuous wavelet transform (CWT) were computed in order to form the feature vectors of US bladder and phantom images. In this study, it is observed that the proposed automatic threshold scheme for ISOM network has significantly eliminated the former ISOM network’s threshold problem for US images. This improvement enhances the robustness of ISOM algorithm. Obtained results show that ISOM with AT value has similar segmentation performance with Kohonen’s network.
Keywords - Segmentation of ultrasound images, neural networks, incremental selforganizing map, continuous wavelet transform, fast Fourier transform.
1. Introduction
Continuous developments and inherently hazardous-free structure of ultrasonography preserve its importance in diagnosis of diseases. Since it is an operator-dependent diagnosis technique, obtained results may be interpreted in different manners. In this study, realization of automatic tissue segmentation was aimed and a diagnosis method which may be useful for especially inexperienced operators is presented. For this purpose, interviews with radiologists were made and their ideas and expectations were taken into account.
The determination of features which represent the tissues best is still a serious problem which affects the results of segmentation directly. There are many types of feature extraction methods in literature. However, there is not any unique method that fits all tissue types. Popular feature extraction methods include auto-correlation [1], gray-level based approaches [2, 3], co-occurrence matrices [4], wavelet [5], discrete Fourier [6], and discrete cosine [7] transforms. Main problems of image processing applications come from the large number of features with position and scaling changes. Therefore, more clever and robust feature extraction methods are needed.
Segmentation of ultrasound (US) images is a critical subject in medical image analysis. Although the features are determined well, the segmentation algorithm must be chosen well enough to obtain good results. Up to now, various schemes have been introduced in order to accomplish this task.
In our study, two different self-organizing map (SOM) networks were used; Kohonen’s SOM [8] and I2SOM network. The I2SOM is an improved version of ISOM [9] network with the addition of an automatic threshold function that produces a suitable threshold value and a node-coloring scheme that shows the vicinity of nodes visually in multi-dimensional feature space. 2D-FFT and 2D-CWT were comparatively investigated to form the features of tissues.
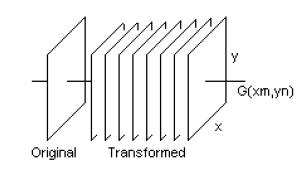
Figure 1. Formation of nine-dimensional 2D-CWT features

Figure 2. Processing blocks in segmentation
2. Methods
2.1 2D fast Fourier transform
FFT is a transform that provides frequency content of a signal. In this study, 2D-FFT of a 5x5 window of pixel data centered on the pixel of interest is calculated to form the feature vectors of US images. Absolute values of nine more distinctive complex low-frequency coefficients were considered as features from a total of 25 coefficients. Segmentation time increases dramatically for larger window sizes.
2.2 2D continuous wavelet transform
CWT is a convenient transform for non-stationary signals. FFT shows the frequency spectrum of signals but it can not detect the time interval in which any frequency component occurs [10]. By using 2D-CWT, spacescale (time-frequency) representation of a signal can be obtained which means a higher information level. By using CWT as feature extraction method, macro evaluation of the image rather then pixel based evaluation is provided. An important parameter related to CWT is the scale parameter. When the scale value is high, low frequency components of image are becoming clear and when the scale value decreases, high frequency components (details) in the image can be observed well.
In this study, 2D-CWT of whole US image was calculated for eight different scale parameters. Thus, eight transformed images were obtained from the original image. For each pixel, the intensity values from the nine images were considered together and, therefore, generating a nine-dimensional feature vector, to be also used as input into the classifiers. Figure 1 shows the formation of feature vectors. Here, x and y show coordinates whereas G(Xm,Yn) denotes the pixel values of the original and transformed images.
After forming the required feature vectors, self-organization process is accomplished in order to arrange network nodes in multi-dimensional feature space. Figure 2 depicts the segmentation process.
2.3 Automatic threshold
The main difference of presented network from its former versions is the automatic threshold (AT) value computed by a simple function before starting to self-organization stage. In ISOM, threshold values were being determined manually and by method of trial and error. When using different US images or different training sets for the same image, recalculation of threshold was required and it was really a time-consuming process. By using automatic threshold function, a standard calculation method is generated for the segmentation of US images so, it becomes possible to measure the effects of different parameters on the segmentation result in an objective way. Otherwise, since threshold is computed manually, any change in the segmentation result may happen because of the chosen threshold value rather than the parameters themselves. The robustness of algorithm is provided. I2SOM’s automatic threshold value is defined as follows:

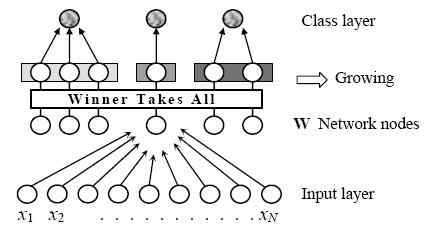
Figure 3. Structure of I2SOM, N is the feature space dimension
In Equation 1, X is the feature vector matrix of size M?N. Each row of the matrix is constituted by the elements of the feature vectors, hence, X holds N-dimensional M feature vectors. mj denotes the mean value of the features on column j.
In fact, AT value represents the distribution of feature vectors in multi-dimensional feature space. Although AT function was simply defined, it shows high performance in generating proper threshold values depending on the number of features (dimension of vectors) and distribution in the feature space. AT function is calculated for different US images and it has been observed that the proposed function is capable of generating a reference threshold.
2.4. Node coloring
In order to visualize the difference between tissue structures, a node-coloring scheme based on interpolation technique was used. The mathematical formulation of the method is expressed in Equation 2 where n denotes the nth node in the network. C(n) denotes the gray tone of the node number n. d(n,a) and d(n,b) are the Euclidean distances in the feature space between the node n and the nodes a and b, respectively. C(a) and C(b) denotes the color values of the two most distant nodes (a and b) in the network. In this scheme, first of all, two most distant nodes (a and b) found by calculating Euclidean distances in the network are colored with 0 and 255 gray values. Then, the remaining nodes’ colors are assigned according to their distances to the formerly colored two nodes. Finally, the segmented image colors are formed according to related nodes’ colors.

3. Improved Incremental Self-Organizing Mp (I2SOM)
Artificial neural networks (ANNs) have been used widely in many image processing applications. In supervised learning methods, network modifies its parameters to decrease the difference between its own output and desired output. Training set of network is constituted with the feature vectors that are randomly chosen in equal numbers from every class.
In unsupervised learning, network modifies its parameters by analyzing the class distributions in feature space. There is no desired output in this method or desired outputs are not used in the training algorithm. Kohonen’s SOM and I2SOM networks which are used in this study are both examples of unsupervised networks.
I2SOM network used in this study is a two-layer, self-organizing incremental network. It is an improved version of formerly developed ISOM [9]. Therefore, the main structure of I2SOM that is showed in Figure 3 is the same as ISOM.
Before the training of I2SOM network, the pixels which will be used in feature extraction process are selected from the image at random. It has been observed that using only a small fraction of image pixels provides sufficient segmentation results. Thus, in the training stage, a few image pixels were taken into account rather than taking all of them.
Initially, a feature vector is randomly chosen from the training set, and is assigned as the first node of the network. Then, the learning rate is set. The learning algorithm steps can be summarized as follows:
Step 1 - Take a feature vector from the training set.
Step 2 - Compute the Euclidean distances between this input feature vector and the nodes in the network, and find the minimum distance.
Step 3 - If the minimum distance is higher than the automatic threshold value, include the input vector as a new node of I2SOM. Assign a counter to this new node and set the counter value to one, then go back to the first step. Otherwise, update the weights of the nearest node (winner) according to Eq.(3). Increase the counter value of the winner node by one. Decrease the learning rate.
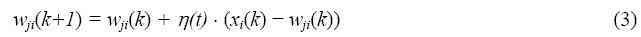
In Equation 3, wji is the ith weight of the jth (winner) node nearest to the input vector, xi is the ith element of the input vector, ?(t) is the learning rate (0 < ?(t) < 1), and k is the iteration number. ?(t) becomes smaller as time (t) increases.
Step 4 - Go to step 1 until all feature vectors are exhausted.
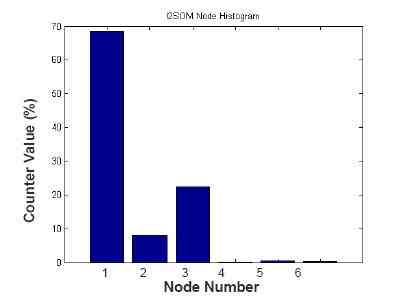
After the completion of training period, the nodes which have lower counter values can be removed from the network. These nodes can be determined via node histogram of I2SOM in which x-axis shows the nodes’ number and y-axis shows the counter values associated with these nodes. Removing process is done by assigning the labels of the nearest nodes that have greater counter values to those removed nodes. If the counter value of a node is too low, it means that this node represents a small portion of image pixels. Without the removal process, as every node of I2SOM represents a class, segmentation time will become higher. In Figure 4, a sample node histogram belonging to the phantom US image can be seen. Although the network produced six nodes, the nodes #4, 5 and 6 have counter values below 1%. Thus, they can be removed from I2SOM network.
4. Computer Simulations
In the study, US phantom and bladder images (Figures 5(a, b)) were segmented by using Kohonen’s SOM and I2SOM networks. 2D-FFT and 2D-CWT (Gaussian wavelet) were used in feature extraction processes of both images. The simulations were performed on 2 GHz PC by using MATLAB 6.0. Bladder image was segmented into three classes. The phantom image [12] was segmented into two classes.
Segmentation results can be seen in Figures 6(a?d) and Figures 7(a?d). Related parameters like training time (TT), segmentation time (ST) and number of generated nodes (NoN) can be seen in Table 1.
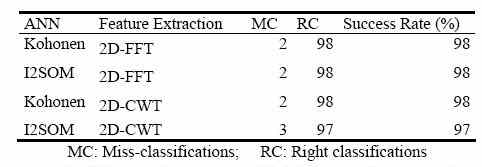
In order to show the performances of Kohonen and I2SOM networks comparatively, 100 test feature vectors (50 for each class) were formed from the phantom image. The same test set was used for both networks. Performance comparison was made between Kohonen’s SOM and I2SOM according to the results presented in Table 2.
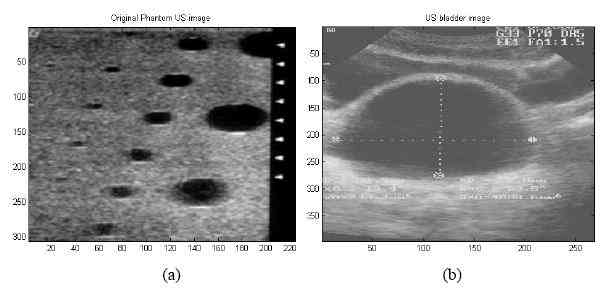
Figure 5. Ultrasound (a) phantom image, (b) bladder image.

Figure 6. Segmented bladder image by (a) Kohonen, (b) I2SOM network using 2D-FFT features. Segmented bladder image by (c) Kohonen, (d) I2SOM network using 2D-CWT features
5. Conclusions
It is observed that I2SOM network is capable of segmenting the phantom image as good as Kohonen’s SOM. In fact, segmentation performance is too sensitive to the training set. Therefore for another set, performance of both ANNs will differ as expected. Although Kohonen’s SOM is a fast algorithm, it is not an incremental network. Besides, the strategy of the learning algorithm of the Kohonen network makes the output nodes locate in the feature space homogenously rather than concentrating on class boundaries. This structure may require excessive number of nodes in the network. Moreover, the problem of determining the optimum number of nodes and network topology is another disadvantage of the Kohonen network. Again, network nodes may not be capable of representing the classes well enough if network parameters such as the neighborhood and learning rate are not properly chosen. However, since I2SOM is an incremental network, it automatically determines the proper number of nodes required for the segmentation. Furthermore, AT function significantly eliminated the threshold sensitivity of network’s former versions in the segmentation of US images. I2SOM is able to detect different clusters within a given training set by extracting a reference AT value depending on the statistics of features.
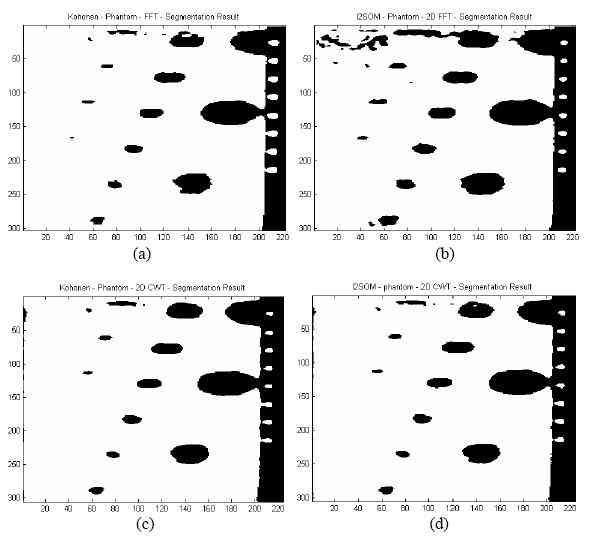
Figure 7. Segmented phantom image by (a) Kohonen using 2D-FFT features, (b) I2SOM network using 2D-FFT features, (c) Kohonen 2D-CWT features, and (d) I2SOM using 2D-CWT features
Table 1. Segmentation results of ANNs
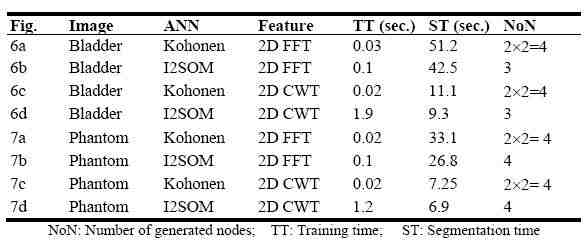
Table 2. Performance results of ANNs for the phantom image
According to the segmentation results in Table 1, it can be observed that segmentation of the US images using 2D-CWT features accomplishes in a shorter time compared to that of 2D-FFT features. However, it must be noted that, CWT was applied to the whole image whereas FFT was applied to sub-images that have windows sizes of 5?5. Thus, the main time difference was generated because of these different approaches in producing feature vectors.
ISOM and I2SOM have the same structures and training algorithms. Hence, they generate similar results for the same threshold values. Segmentation results are affected by the threshold values for both networks. In the training of ISOM, the threshold value can be determined after a few trials. The following procedure can be used to estimate a threshold value: First, the user determines two similar tissues in the image. Then, two feature vectors are manually extracted by using the mouse of the computer. Lastly, the threshold value is determined as follows:
Threshold ? ||V1 - V2|| V1 = [I11, ... IN1] V2 = [I12, ... IN2] (4)
where V1 and V2 are the feature vectors belonging to the first and the second tissues respectively, Iik represents the ith feature selected for the kth tissue, N is dimension of the feature vectors. This search increases the training time of the ISOM. In I2SOM, the threshold value is automatically determined before the training.
In the training of I2SOM, there is not any neighborhood analysis as in Kohonen network. Thus, the training algorithm of I2SOM is not complex as can be easily observed from the training algorithm steps. It is observed that Kohonen network gives similar results as I2SOM. However, many trials are realized to find the optimal parameters (such as the size of network and the neighborhood) of the Kohonen network. In this study, Kohonen network’s segmentation results obtained after optimal parameter search are presented in Figs. 6, 7.
Obtained results show that, I2SOM is highly a promising network for the segmentation of US images. During studies, proposed network was also tested on different medical US images like abdomen, breast and prostate [13]. It has been observed that I2SOM generated satisfactory results for all those images. Thus, it can be a useful tool for inexperienced operators working in this area.
References
[1] D.R. Chen, R.F. Chang, Y.L. Huang, “Breast Cancer Diagnosis Using Self-Organizing Map For Sonography,” World Federation for Ultrasound in Med. & Biol., Vol. 26(3), pp. 405–411, 2000.
[2] C. Loizou, C. Christodoulou, C.S. Pattichis, R. Istepanian, M. Pantziaris, A. Nicolaides, “Speckle Reduction in Ultrasonic Images of Atherosclerotic Carotid Plaque,” 14th International IEEE Conference on Digital Signal Processing, pp. 525-528, 2002.
[3] S. Pavlopoulos, E. Kyriacou, D. Koutsouris, K. Blekas, A. Stafylopatis, P. Zoumpoulis, “Fuzzy Neural Network Computer Assisted Characterization of Diffused Liver Diseases Using Image Texture Techniques on Ultrasonic Images,” IEEE Trans. Eng. in Medicine and Biology Magazine, Vol. 19(1), pp. 39-47, 2000.
[4] A. Kadyrov, A. Talepbour, M. Petrou, “Texture Classification With Thousands of Features,” 13th British Machine Vision Conference, Cardiff-UK, 2002.
[5] N.M. Rajpoot, “Texture Classification Using Discriminant Wavelet Packet Subbands,” 45th IEEE Midwest Symposium on Circuits and Systems, Tulsa-USA, 2002.
[6] Y. Tao, V. Muthukkumarasamy, B. Verma, M. Blumenstein, “A Texture Feature Extraction Technique Using 2D–DFT and Hamming Distance,” 5th International Conference on Computational Intelligence and Multimedia Applications, Xi’an-China, 2003. Ultrasound Image Segmentation by Using Wavelet and SOM Z. Iscan, M.N. Kurnaz, Z. Dokur, and T. Olmez 190
[7] G. Sorwar, A. Abraham, L.S. Dooley, “Texture Classification Based on DCT and Soft Computing,” 10th IEEE International Conference on Fuzzy Systems, 2001.
[8] T. Kohonen, Self-Organization and Associative Memory, Springer-Verlag, New York, 1988.
[9] M.N. Kurnaz, Z. Dokur, T. Olmez, “Segmentation of Ultrasound Images by Using an Incremental Self- Organized Map,” 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Istanbul-Turkey, 2001.
[10] R. Polikar, “Fundamental Concepts & An Overview of the Wavelet Theory,” Tutorial, http://users.rowan.edu/~polikar/WAVELETS/WTpart1.html, 1996.
[11] Z. Dokur, “Classification of ECG Beats by Using Artificial Neural Networks and Genetic Algorithms,” Ph.D. Dissertation (in Turkish), Istanbul Technical University, Institute of Science & Technology, 2000.
[12] http://www.fantom.suite.dk/571.htm
[13] Z. Iscan, “Segmentation Of Ultrasound Images by Using Artificial Neural Networks,” M.Sc. Thesis (in Turkish), Istanbul Technical University, Institute of Science & Technology, 2005.