Исходный текст данной статьи находится по URL: http://ieeexplore.ieee.org/iel5/9009/28608/01279845.pdf (необходима регистрация)

Перевод выполнил: магистр ДонНТУ Михалец В.В.

Обработка Информации Нейронными Сетями - Письма и Обзоры

Vol. 10, Nos. 8-9, Aug.-Sept. 2006

ПИСЬМО

Сегментация Ультразвуковых Изображений с использованием Вейвлет Преобразования и Самоорганизующейся Нейронной Сети

Zafer Iscan, Mehmet Nadir Kurnaz, Zumray Dokur и Tamer Olmez

Отделение Электроники и Коммуникационного Инжинеринга Станбульский Технический Университет, 34469 Станбул, Турция

E-mail: zafer@ehb.itu.edu.tr

(Подписано 21 Апреля и 7 Июля 2006г.; принято 8 Августа 2006г.)

Реферат - эта статья описывает улучшенную наращиваемую самоорганизующуюся сеть (УНСОС), которая использует автоматическое определение порогового значения (ПЗ) для сегментации ультразвуковых изображений (УЗ). Чтобы показать действенность предложенной схемы, было проведено ее сравнение с самоорганизующейся сетью Кохонена (СОСК). Двухмерное (2D) быстрое преобразование Фурье (БПФ) и двухмерное (2D) непрерывное вейвлет преобразование (НВП) были вычислены, чтобы формировать векторы признаков УЗ изображения мочевого пузыря и фантома. В этом исследовании было определено, что предложенная схема для автоматического определения порога для НСО сети значительно устранила прежнюю проблему по определению порогового значения сети для УЗ изображений. Это усовершенствование увеличивает устойчивость к ошибкам алгоритма НСОС. Полученные результаты показывают, что НСОС с автоматическим определением ПЗ имеет такое же качество выполнения сегментации, что и сеть Кохонена.

Ключевые слова: сегментация УЗ изображений, нейронные сети, наращиваемая самоорганизующаяся сеть, непрерывное вейвлет преобразование, быстрое преобразование Фурье.

1. Вступление

Непрерывное развитие и неотъемлемая структурная безопасность ультрасонографии сохраняет ее важность в диагностике болезней. Так как это зависящий от оператора вид диагностики, полученные результаты могут интерпретироваться в различных манерах. В этом исследовании целью была реализация автоматической сегментации ткани, а также приводится метод диагностики, который может быть полезен для особенно неопытных операторов. Для этой цели, были проведены собеседования с радиологами и их предложения и ожидания были взяты в рассмотрение.

Определение признаков, которые характеризуют ткани лучше всего - все еще серьезная проблема, которая непосредственно влияет на результаты сегментации. Есть много методов извлечения признаков, описанных в литературе. Однако, нет уникального метода, который соответствовал бы всем типам ткани. Популярные методы извлечения признаков включают автокорреляцию [1], подходы, основанные на анализе уровней серого [2, 3], матрицы совместной встречаемости [4], вейвлеты [5], дискретное преобразование Фурье [6] и дискретные косинус преобразования [7] . Главные проблемы программ, обрабатывающих изображения, вознивают из-за большого числа признаков, которые меняются в зависимости от масштаба и позиции. Поэтому, необходимы более устойчивые и «умные» методы для извлечения признаков.

Сегментация ультразвукых изображений – критически важный этап в медицинском анализе изображений. Даже если признаки определены хорошо, алгоритм сегментации должен быть выбран достаточно аккуратно для получения хороших результатов. К настоящему времени различные схемы алгоритма сегментации были представлены, чтобы выполнить эту задачу.

В нашем исследовании использовались две различные сети карт самоорганизации (СОС): сеть Кохонена [8] и УНСО сеть. УНСО сеть - улучшенная версия НСО [9] сети с дополнением автоматической пороговой функции, которая вычисляет подходящее пороговое значение, и схемы окрашивания узлов, показывающей окрестности узла визуально в многомерном пространстве признаков. 2D-БПФ и 2D-НВП были сравнительно исследованы для формирования признаков тканей.

Рисунок 1. Формирование признаков с помощью 2D-НВП в 9-ти мерном пространстве

Рисунок 2. Блоки вычислений в алгоритме сегментации

2. Методы

2.1 2D Быстрое преобразование Фурье

БПФ – это преобразование, которое извлекает частотное содержание сигнала. В этом исследовании, 2-хмерное БПФ скользящего окна в 5x5 пикселей, с центром на интересующем пикселе было просчитано, чтобы сформировать векторы признаков УЗ изображения. Абсолютные значения девяти наиболее отличающихся комплексных коэффициентов низкой частоты рассматривались как признаки от общего количества в 25 коэффициентов. Время сегментации увеличивается очень быстро для больших размеров окна.

2.2 2D Непрерывное вейвлет преобразование

НВП – это удобное преобразование для нестационарных сигналов. БПФ показывает спектр частоты сигналов но оно не может обнаружить временной интервал, за который появляется какая-то частотная составляющая [10]. Используя 2D-НВП, пространственно-масштабное (частотно-временное) представление сигнала может быть получено, что означает более высокий информационный уровень. Используя НВП, как метод извлечения признаков, производится макро-оценка изображения, а не оценка, основанная на анализе отдельного пиксела. Важный параметр, связанный с НВП - параметр масштаба. Когда значение параметра масштаба высоко, низко-частотные составляющие изображения становятся отчетливыми и когда значение параметра масштаба уменьшается, высоко-частотные составляющие (детали) изображения могут быть хорошо выделены.

В этом исследовании, 2D-НВП целого УЗ изображения было рассчитано для восьми различных параметров масштаба. Таким образом, восемь преобразованных изображений было получено из первоначального изображения. Для каждого пиксела значения интенсивностей от девяти изображений рассматривались вместе и, поэтому, был получен девятимерный вектор признаков, который также использовался как вход в классификаторы. Рисунок 1 показывает формирование векторов признаков. Здесь, x и y – координаты, тогда как G(x_m, y_n) обозначает значения пикселов оригинального и преобразованных изображений.

После формирования требуемых векторов признаков, выполняется процесс самоорганизации, чтобы упорядочить узлы сети в многомерном пространстве признаков. Рисунок 2 изображает процесс сегментации.

2.3 Автоматическое определение порога

Главное отличие представленной сети от ее прежних версий – это автоматическое определение порогового значения (ПЗ), вычисляемое простой функцией перед стартом стадии самоорганизации. В НСОС значения порога определялись вручную и методом проб и ошибок. При использовании различных УЗ изображений или различных наборов обучения для того же самого изображения, требовался пересчет значения порога, и это был действительно отнимающий много времени процесс. Используя автоматическую пороговую функцию, получен стандартный метод вычислений для сегментации УЗ изображений. Таким образом, стало возможным ограничить влияние различных параметров на результат сегментации объективным способом. Иначе, если порог вычисляется вручную, любое изменение в результате сегментации может случиться из-за изменения выбранного значения порога, а не из-за непосредственного изменения самих параметров. Алгоритм обеспечивает устойчивость к ошибкам и помехам. Автоматическое значение порога для УНСОС определяется следующим образом:

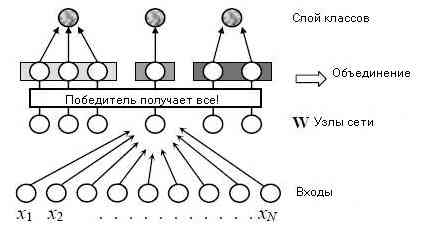
Рисунок 3. Структура УНСОС, N - размерность пространства признаков

В формуле 1 X - матрица признаков размера M*N. Каждый ряд матрицы составлен из элементов векторов признаков, следовательно, X содержит М N-размерных векторов признаков. M_j обозначает среднее значение признака по колонке j.

Фактически, ПЗ представляет распределение векторов признаков в многомерном пространстве признаков. Хотя выражение функции ПЗ было просто определено, оно показывает высокое качество в вычислении надлежащего значения порога в зависимости от числа признаков (размерности векторов) и распределения в пространстве признаков. Функция ПЗ была вычислена для различных УЗ изображений, и было отмечено, что предложенная функция способна определять надлежащее ПЗ.

2.4. Окрашивание узлов

Чтобы визуализировать различие между структурами ткани, использовалась схема окрашивания узлов, базируемая на техника интерполяции. Математическая формулировка метода выражена в формуле 2, где n обозначает n-ый узел в сети. C(n) обозначает серый тон узла n. d (n, a) и d (n, b) - эвклидовые расстояния в пространстве признаков между узлом n и узлами а и b, соответственно. C(a) и C(b) обозначает значения цветов двух самых отдаленных узлов (а и b) в сети. В этой схеме, прежде всего, два самых отдаленных узла (а и b), найденных вычислением эвклидовых расстояний в сети, окрашываются серыми тонами «0» и «255». Тогда, цвета оставшихся узлов назначаются согласно их расстояниям к двум прежде окрашенным узлам. Наконец, цвета сегментированного изображения формируются согласно цветам соответствующих узлов.

3. Улучшенная наращиваемая самоорганизующаяся сеть (УНСОС)

Искусственные нейронные сети (ИНС) широко используются во многих приложениях по обработке изображений. В контролируемых методах обучения, сеть изменяет свои параметры, чтобы уменьшить различие между ее собственным выходом и желаемым выходом. Наборы для обучения сети состоят из векторов признаков, которые случайно выбираются в равных количествах от каждого класса.

В обучении без учителя, сеть изменяет свои параметры, анализируя распределения классов в пространстве признаков. В этом методе нет никакого желаемого выхода, или желаемые выходы не используются в алгоритме обучения. Сеть Кохонена и УНСОС, которые используются в этом исследовании - примеры сетей, обучаемых без учителя.

УНСОС, используемая в этом исследовании – это двухслойная, самоорганизующаяся наращиваемая сеть. Это улучшенная версия прежде разработанной НСОС [9]. Поэтому, главная структура УНСОС, которая показана на рисунке 3, та же, что у НСОС.

Перед обучением УНСОС, пикселы, которые будут использоваться в процессе извлечения признаков, случайно отбираются из изображения. Было замечено, что использование только маленькой доли из общего числа пикселов изображения обеспечивает достаточные результаты сегментации. Таким образом, на стадии обучения, только некоторые пикселы изображения принимаются во внимание, но не все.

Первоначально, вектор признаков случайно выбирается из набора обучения, и назначается как первый узел в сети. Затем устанавливается скорость обучения. Шаги алгоритма обучения могут быть подытожены следующим образом:

Шаг 1 - Взять вектор признаков из обучающего множества.

Шаг 2 - Вычислить эвклидовые расстояния между этим входным вектором признаков и узлами сети, найти минимальное расстояние.

Шаг 3 - Если минимальное расстояние выше чем автоматическое пороговое значение, включить входной вектор как новый узел УНСОС. Назначить счетчик этому новому узлу, и установить его равным «0», возвратиться к первому шагу. Иначе, модернизировать веса самого близкого узла (победителя) согласно выражению (3). Увеличить значение счетчика узла-победителя на «1». Уменьшить скорость обучения.

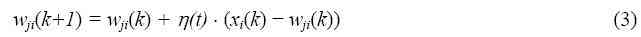
В уравнении 3, w_ji - i-ый вес j-го (победителя) узла, самого близкого ко входному вектору, x_i - i-ый элемент входного вектора, ?(t) – скорость обучения (0 < ?(t) < 1), и k- итеративное число. ? (t) становится меньше как время (t) увеличивается.

Шаг 4 - Возвращение к шагу 1 пока все обучающие вектора признаков не будут обработаны.

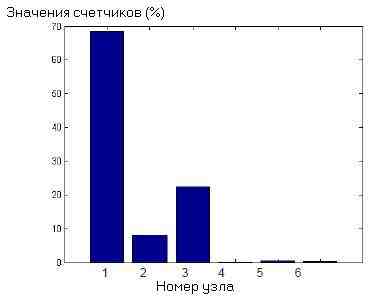
После завершения периода обучения, узлы, которые имеют более низкие значения счетчиков, могут быть удалены из сети. Эти узлы могут быть определены с помощью гистограммы, в которой ось X показывает номер узла, а ось Y показывает значения счетчика, связанного со своим узлом. Процесс удаления осуществляется назначением меток самых близких узлов, которые имеют большие значения счетчиков, удаляемым узлам. Если значение счетчика узла слишком мало, это означает, что этот узел представляет маленькую часть пикселов изображения. Без процесса удаления, поскольку каждый узел УНСОС представляет класс, время сегментации будет больше. На рисунке 4 можно видеть гистограмму счетчиков узлов принадлежащую УЗ изображению фантома. Хотя сеть произвела шесть узлов, узлы 4, 5 и 6 имеют значения счетчиков ниже 1 %. Таким образом, они могут быть удалены из УНСОС сети.

4. Компьютерное моделирование

В исследовании УЗ изображения фантома и мочевого пузыря (рисунок 5 (а, b)) были сегментированы, используя СОС Кохонена и УНСОС. 2D-БПФ и 2D-НВП (гауссовский вейвлет) использовались в процессе извлечения признаков обоих изображений. Моделирование было выполнено на PC на 2 ГГц, используя MATLAB 6.0. Изображение мочевого пузыря было сегментировано на три класса. Изображение фантома [12] было сегментировано на два класса.

Результаты сегментации приведены на рисунке 6 (a?d) и рисунке 7 (a?d). Связанные параметры, такие как время обучения (ВО), время сегментации (ВС) и число полученных узлов (ЧУ) приведены в таблице 1.

Чтобы показать качество работы сетей Кохонена и УНСОС в сравнении, 100 испытательных векторов признаков (50 на каждый класс) были сформированы из изображения фантома. Этот испытательный набор использовался для обеих сетей. Сравнение качества работы было сделано между СОС Кохонена и УНСОС согласно результатам, представленным в таблице 2.

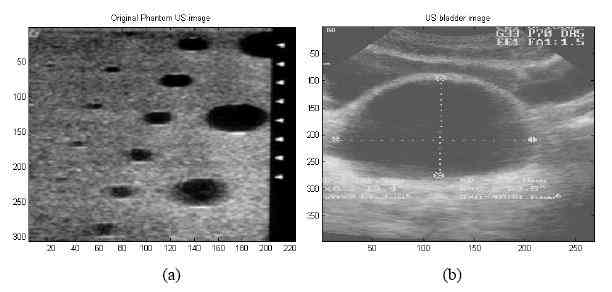
Рисунок 5. Ультразвуковое изображение (a) фантома, (b) мочевого пузыря.

Рисунок 6. Сегментированное изображение мочевого пузыря сетью (a) Кохонена, (b) УНСОС с использованием 2D-БПФ признаков. Сегментированное изображение мочевого пузыря сетью (c) Кохонена, (d) УНСОС с использованием 2D-НВП признаков.

5. Выводы

Было определено, что УНСО сеть способна к сегментации изображения фантома столь же хорошо, как и сеть Кохонена. Фактически, качество выполнения сегментации слишком чувствительно к набору обучения. Поэтому для другого набора качество работы обоих ИНС будет отличаться от ожидаемого. Хотя сеть Кохонена – это быстрый алгоритм, она – не наращиваемая сеть. Кроме того, стратегия обучения по алгоритму сети Кохонена заставляет выходные узлы распределиться в пространстве признаков гомогенно, а не концентрироваться на границах классов. Эта структура может требовать чрезмерного числа узлов в сети. Кроме того, проблема определения оптимального числа узлов и топологии сети – другой недостаток сети Кохонена. Снова, узлы сети могут быть не способны к представлению классов достаточно хорошо, если параметры сети, типа соседства и скорости обучения, не выбраны должным образом. В то же время, так как УНСОС - возрастающая сеть, то она автоматически определяет надлежащее число узлов, требуемых для сегментации. Кроме того, функция определения ПЗ значительно устраняет пороговую чувствительность прежних версий сети для сегментации УЗ изображений. УНСОС способна обнаруживать различные группы в пределах данного обучающего множества, извлекая соответствующее ПЗ в зависимости от статистики признаков.

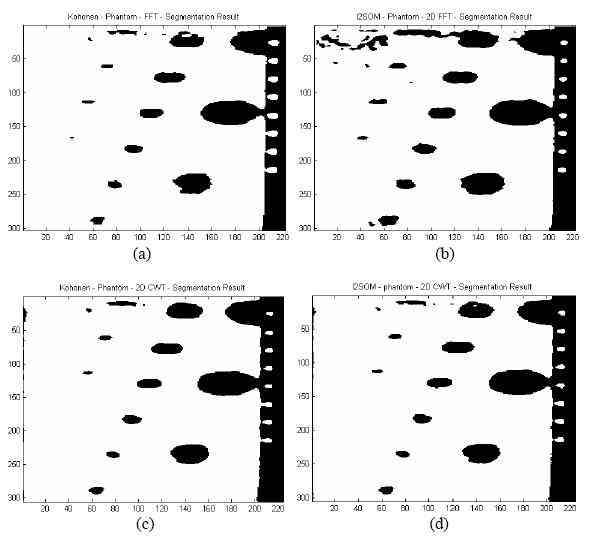
Рисунок 7. Сегментированное изображение фантома сетью (a) Кохонена, (b) УНСОС с использованием 2D-БПФ признаков. Сегментированное изображение фантома сетью (c) Кохонена, (d) УНСОС с использованием 2D-НВП признаков.

Таблица 1. Результаты сегментации с помощью ИНС

Таблица 2. Результаты качества сегментации с помощью ИНС для изображения фантома

ИНС	Извлечение признаков	Ошибочная классификация	Правильная классификация	Процент успеха (%)
Кохонен	2D-БПФ	2	98	98
УНСОС	2D-БПФ	2	98	98
Кохонен	2D-НВП	2	98	98
УНСОС	2D-НВП	3	97	97

 

Согласно результатам сегментации в таблице 1, видно, что сегментация УЗ изображений с использованием 2D-НВП признаков выполняется в более короткое время по сравнению с 2D-БПФ признаками. Однако, должно быть отмечено, что 2D-НВП преобразование было применено к целому изображению, тогда как 2D-БПФ было применено к подизображениям, которые имели размеры окна 5*5 пикселей. Таким образом, главная разница во времени была произведена из-за этих различных подходов в создании векторов признаков.

НСОС и УНСОС имеют ту же самую структуру и алгоритмы обучения. Следовательно, они дают одинаковые результаты для одинаковых ПЗ. На результаты сегментации влияют значения порогов для обеих сетей. При обучении НСОС пороговые значения могут быть определены после нескольких испытаний. Следующая процедура может использоваться для оценки порогового значения: сначала, пользователь определяет две одинаковые ткани в изображении; затем, два вектора признаков извлекаются вручную с использованием мыши компьютера; наконец, пороговое значение определяется так:

Порог ? ||V₁ - V₂||      V₁ = [I₁¹, ... I_N¹]      V₂ = [I₁², ... I_N²]     (4)

где V₁ и V₂ - векторы признаков, принадлежащие первому и второму типу ткани соответственно, I_i^k представляет i-ый признак, отобранный для k-го типа ткани, N – размерность векторов признаков. Этот поиск увеличивает время обучения НСОС. В УНСОС пороговое значение автоматически определяется перед обучением.

В обучении УНСОС нет никакого анализа окрестностей как в сети Кохонена. Таким образом, алгоритм обучения УНСОС не сложен, как может быть легко видно из шагов алгоритма обучения. Сеть Кохонена дает сходные результаты с УНСОС. Однако, много попыток производится для нахождения оптимальных параметров (размера сети и соседства) сети Кохонена. В это исследовании, результаты сегментации сетью Кохонена, полученные после поиска оптимальных параметров, представлены на рисунках 6, 7.

Полученные результаты показывают, что УНСОС - многообещающая сеть для сегментации УЗ изображений. Во время исследования, предложенная сеть была также проверена на различных медицинских УЗ изображениях, таких как, живот, грудь и простата [13]. Было отмечено, что УНСОС произвела удовлетворительные результаты для всех этих изображений. Таким образом, она может быть полезным инструментом для неопытных операторов, работающих в этой области.

Ссылки

[1] D.R. Chen, R.F. Chang, Y.L. Huang, “Breast Cancer Diagnosis Using Self-Organizing Map For Sonography,” World Federation for Ultrasound in Med. & Biol., Vol. 26(3), pp. 405–411, 2000.

[2] C. Loizou, C. Christodoulou, C.S. Pattichis, R. Istepanian, M. Pantziaris, A. Nicolaides, “Speckle Reduction in Ultrasonic Images of Atherosclerotic Carotid Plaque,” 14th International IEEE Conference on Digital Signal Processing, pp. 525-528, 2002.

[3] S. Pavlopoulos, E. Kyriacou, D. Koutsouris, K. Blekas, A. Stafylopatis, P. Zoumpoulis, “Fuzzy Neural Network Computer Assisted Characterization of Diffused Liver Diseases Using Image Texture Techniques on Ultrasonic Images,” IEEE Trans. Eng. in Medicine and Biology Magazine, Vol. 19(1), pp. 39-47, 2000.

[4] A. Kadyrov, A. Talepbour, M. Petrou, “Texture Classification With Thousands of Features,” 13th British Machine Vision Conference, Cardiff-UK, 2002.

[5] N.M. Rajpoot, “Texture Classification Using Discriminant Wavelet Packet Subbands,” 45th IEEE Midwest Symposium on Circuits and Systems, Tulsa-USA, 2002.

[6] Y. Tao, V. Muthukkumarasamy, B. Verma, M. Blumenstein, “A Texture Feature Extraction Technique Using 2D–DFT and Hamming Distance,” 5th International Conference on Computational Intelligence and Multimedia Applications, Xi’an-China, 2003. Ultrasound Image Segmentation by Using Wavelet and SOM Z. Iscan, M.N. Kurnaz, Z. Dokur, and T. Olmez 190

[7] G. Sorwar, A. Abraham, L.S. Dooley, “Texture Classification Based on DCT and Soft Computing,” 10th IEEE International Conference on Fuzzy Systems, 2001.

[8] T. Kohonen, Self-Organization and Associative Memory, Springer-Verlag, New York, 1988.

[9] M.N. Kurnaz, Z. Dokur, T. Olmez, “Segmentation of Ultrasound Images by Using an Incremental Self- Organized Map,” 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Istanbul-Turkey, 2001.

[10] R. Polikar, “Fundamental Concepts & An Overview of the Wavelet Theory,” Tutorial, http://users.rowan.edu/~polikar/WAVELETS/WTpart1.html, 1996.

[11] Z. Dokur, “Classification of ECG Beats by Using Artificial Neural Networks and Genetic Algorithms,” Ph.D. Dissertation (in Turkish), Istanbul Technical University, Institute of Science & Technology, 2000.

[12] http://www.fantom.suite.dk/571.htm

[13] Z. Iscan, “Segmentation Of Ultrasound Images by Using Artificial Neural Networks,” M.Sc. Thesis (in Turkish), Istanbul Technical University, Institute of Science & Technology, 2005.