Миргоязова Антонина Владимировна

О работе ...

         На данной странице приняты такие сокращения:

• УРБС – универсальный рельсобалочный прокатный стан;
• АСУ ТП – автоматическая система управления технологическим процессом;
• САУ – система автоматического управления;
• ЛК-регулятор – линейно-квадратичный регулятор;
• ЛКГ-регулятор – линейно-квадратичный гауссовский регулятор;
• ППП – пакет прикладных программ.

         Производство металла имеет большое значение для развития народного хозяйства и роста благосостояния людей. От успешного развития металлургии в значительной мере зависит обеспечение металлом машиностроения, строительства, транспорта, сельского хозяйства и других областей народного хозяйства.
         Технологический процесс получения готового проката является завершающей стадией металлургического производства. Через прокатные цеха проходит почти вся сталь, выплавляемая в сталеплавильных цехах, поэтому наряду с увеличением производства проката существует проблема повышения эффективности прокатного производства и качества готового продукта.
         Особенностью развития прокатного производства является переход к непрерывным процессам прокатки.
         Это позволяет существенно увеличить производительность прокатных станов и качество их продукции. Обеспечение непрерывной схемы прокатки требует существенного повышения уровня автоматизации технологических процессов и обеспечения оптимальности управления.
         Управление технологическим процессом, проблема выбора оптимальной технологии связаны с выбором критерия оценки качества. Задачу выбора таких критериев можно определить как задачу определения качества технологического процесса.
         Одним из наиболее полезных критериев, используемых при проектировании оптимальных систем управления, является показатель ошибки, характеризующий отклонение координат системы от требуемых значений. Выбор соответствующего показателя ошибки может существенно повлиять на характеристики системы управления при ее разработке.
         Актуальность системы управления состоит в том, что применяемые в настоящее время в промышленности регуляторы в большинстве случаев не обеспечивают оптимальных режимов работы прокатных станов.
         Целью данной работы является автоматизация синтеза алгоритмов оптимального управления с помощью квадратичного критерия качества процессом прокатки, являющимся многосвязным и многомерным объектом управления. Необходимость рассмотрения многосвязного объекта объясняется взаимовлиянием процессов прокатки в горизонтальном и вертикальном направлениях.

         АСУ ТП, кроме обеспечения управления процессами, которое невозможно организовать при ручном управлении, ориентирована на оптимизацию управления, целью которого является минимизация потерь производительности, материалов, энергоресурсов, качества продукции.
         Для новых рельсобалочных станов функции АСУ ТП охватывают, как правило, большее число задач, чем на реконструируемых прокатных станах, на которых наибольший эффект автоматизация способна обеспечить только при условии модернизации механического и электрического оборудования.
         Последовательное расположение технологического оборудования УРБС и автономный характер протекания технологических процессов на участках печей, клетей, пил горячей резки и холодильников обуславливают декомпозицию АСУ ТП УРБС на три автономные участковые АСУ ТП: участка нагрева заготовок; участка прокатных клетей; участка пил горячей резки и холодильников, в состав которой входит также автоматизированная система оперативного учета и контроля производства.
         Такая структура имеет ряд преимуществ. Она обеспечивает надежное управление отдельными технологическими участками, возможность поэтапного ввода и наращивания задач автоматизации как по вертикали (уровни АСУ), так и по горизонтали (участки стана), хорошо приспособлена к широкому применению микро-ЭВМ.
         Наиболее широкое применение получило управление режимами обжатий по заранее рассчитанным технологами жестким программам режимов прокатки. В то же время существенные положительные результаты можно получить в результате введения в схемы управления оптимизирующих корректирующих воздействий, учитывающих такие переменные факторы, как пластические свойства и температура проката, износ поверхности валков [3].
         Задача жесткости программного управления нажимными механизмами заключается в хранении и выдаче программ прокатки, содержащих значения растворов валков в каждом пропуске, а также формировании команд, обеспечивающих цифровое оптимальное позиционное управление электроприводом нажимного механизма. Управление скоростными режимами при реверсивной прокатке металла в универсальных клетях должно обеспечить захват металла валками клети на заданной линейной скорости захвата, затем разгон валков с металлом до максимальной линейной скорости прокатки и последующее замедление до заданной скорости выброса полосы на рольганги. При этом разгон электропривода нажимного механизма до максимальной скорости и его торможение ведется с постоянными ускорениями.
         Недостатком такого способа является то, что кривая торможения электропривода существенно изменяется под действием таких факторов, как изменение густоты смазки, нестабильность напряжения питания и др.
         Указанных недостатков лишен способ управления, при котором скорость электропривода нажимного механизма на участке торможения не измеряется, а задается в функции оставшегося пути по заданному закону торможения [2].
         При построении математических моделей и алгоритмов управления необходимо рассматривать возможности их реализации с тем, чтобы обеспечить требуемое качество и надежность управления с помощью максимально простых, дешевых и удобных в эксплуатации технических средств.
         Оптимальное функционирование САУ обеспечивается следующим: выбором оптимальной структурой САУ; подготовкой оптимальных программных воздействий или оптимальной структуры задающего устройства; оптимизацией параметров локальных регуляторов. Процедура оптимального синтеза САУ в общем случае направлена на разработку структуры и алгоритмов, наилучшим образом отвечающих требованиям к точности, колебательности и быстродействию переходных процессов; экономичности управления. Эти требования формализуются в виде задачи минимизации интегральных квадратичных функционалов качества. Такая задача может быть решена с помощью принципа максимума Понтрягина, методов классического вариационного исчисления, динамического программирования и других. Применительно к рассматриваемому объекту управления наиболее целесообразным является использование принципа максимума Понтрягина.

         Прокатный стан предназначен для формирования профилей прямоугольного сечения из нагретых металлических заготовок – блюмов. Желаемый профиль обеспечивается с помощью прокатных валков, как показано на рис. 1:

Рисунок 1 – Формирование профиля прямоугольного сечения

         Желаемая форма выдавливается из заготовки двумя парами цилиндрических валков (по одной на каждую из геометрических осей), которые перемещаются с помощью гидравлических приводов.
         Применение гидроприводов объясняется их высокой удельной энергоемкостью, небольшими габаритными размерами и массой, что определяет незначительную инерционность подвижных частей и, следовательно, высокое быстродействие и точность воспроизведения [4]. Гидравлические приводы отличают плавность и устойчивость движения подвижного элемента, простота конструкции, изготовления и эксплуатации, а также большой срок службы в результате самосмазываемости.
         Целью управления является обеспечение постоянства толщины проката по осям х и у в пределах заданных допусков. Отклонения в толщине профиля могут быть вызваны двумя причинами:

• вариацией толщины и твердости заготовки;
• наличием эксцентриситета прокатных валков.

         Для того чтобы уменьшить влияние этих возмущений, необходимо регулировать величину зазора за счет введения контура обратной связи. Поскольку зазор между валками измерить сложно, то вместо измерения толщины профиля измеряется сила нажатия валков.
         Отклонение толщины заготовки от номинального моделируется возмущением в виде "белого" шума wi, пропущенного через фильтр низких частот с передаточной функцией:

                                                                                    (1)

         где KFi - коэффициент усиления;TFi - постоянная времени.
         Возмущение, связанное с эксцентриситетом валков, - это функция, близкая к периодической, с частотой, равной частоте вращения валков. Приемлемая модель – возмущенный "белым" шумом we сигнал на выходе полосового фильтра второго порядка с передаточной функцией:

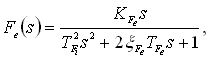                                                                            (2)

         где - коэффициент затухания.
         Сила нажатия валков - это комбинация силы, развиваемой гидравлическим приводом и возмущений, вызываемых эксцентриситетом валков и отклонением толщины заготовки от номинальной.
         На основе этих допущений можно построить следующую структурную схему для модели процесса прокатки по каждой оси:

Рисунок 2 – Структурная схема процесса прокатки по каждой координатной оси х и у

         Здесь u – управление, дельта – отклонение величины зазора от номинального (мм), f –отклонение силы нажатия валков от номинальной, g – коэффициент передачи, we , wi – " белые" шумы, имитирующие возмущения, H(s) – передаточная функция гидропривода:

                                                                            (3)

         Математическую модель разомкнутой системы по каждой из осей можно представить в виде [5]:

                                                                                    (4)

         где х(t)- вектор переменных состояния размерности (n x 1), n=5;u(t)- вектор внешних воздействий размерности (m x 1), m=3:

                                                                                             (5)

         y(t) - вектор выходных переменных размерности (r x 1), r=2:
        

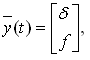                                                                                             (6)

         Выберем критерий оптимальности синтеза автоматического регулятора системы управления прокатным станом такого вида:

                                                                            (7)

         где первое слагаемое критерия характеризует точность работы системы, а второе слагаемое – затраты энергии на управление.
         Очевидно, выбирая соответствующим образом матрицы Q и R, можно получить компромиссное решение между точностью и быстродействием рассматриваемой динамической системы.
         Задача оптимизации состоит в том, чтобы найти совокупность векторов управляющих воздействий, обеспечивающих минимум критерия вида (7):

                                                                                    (8)

         где - оценка вектора переменных состояния системы; K - матрица коэффициентов оптимального управления размерности (mxn).

         Пусть после учета перекрестных связей получена математическая модель, которая описывается уравнениями

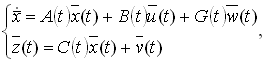                                                                            (9)

   где x(t)- вектор переменных состояния размерности (n x 1), n=10;
         u(t)- вектор управляющих воздействий размерности (m x 1), m=2;
         w(t)- вектор входных возмущений размерности (k x 1), k=4;
         z(t)- наблюдаемый вектор выходных переменных размерности (r x 1), r=4;
         v(t)- вектор шумов измерений размерности (r x 1);
         A(t) - матрица коэффициентов переменных состояния размерности (n x n);
         B(t) - матрица коэффициентов управляющих воздействий размерности (n x m);
         G(t) – матрица коэффициентов входных возмущений размерности (n x k);
         C(t) – матрица измерений выходных величии размерности (r x n).
         Решая эту задачу с помощью принципа максимума Понтрягина, получаем уравнение Риккати:

                                                  (10)

         с граничным условием P(tf)=S. Решение матричного уравнения Риккати необходимо проводить в обратном направлении, от tf к t0 , построив матрицу:

                                                                            (11)

                                                                                    (12)

         На основании полученных в аналитической форме алгоритмов оптимального управления разработано прикладное программное обеспечение для автоматизации аналитического конструирования линейно-квадратичных регуляторов, применяемых при управлении приводами рельсобалочного прокатного стана.
         Результаты работы программы:

Рисунок 3 – Отклонение толщины профиля при разомкнутой (голубой) и замкнутой (черный) одномерной системе для оси х, а затем у

         При замкнутой системе, т.е. при ЛКГ-регуляторе отклонение толщины профиля уменьшается примерно в четыре раза, как для оси х,так и для у.

Рисунок 4 – Реакция на возмущения разомкнутого (голубой) и замкнутого (черный) контуров системы с ЛКГ-регулятором, рассчитанным для многомерной системы без учета перекрестных связей для оси х, а затем у

         Из представленных графиков следует, что характеристики регулирования ухудшились, поскольку максимальное отклонение толщины проката приблизительно в четыре раза больше, чем при моделировании одномерных систем. Следовательно, синтез ЛКГ-регулятора без учета перекрестных связей нельзя признать удовлетворительным при реальном уровне взаимовлияния каналов.
         С целью улучшения качества управления произведем синтез многомерного ЛКГ-регулятора для полной системы с учетом влияния перекрестных связей:

Рисунок 5 – Переходные процессы в разомкнутом (голубой) и замкнутом (черный) контурах управления при использовании в обратной связи многомерного ЛКГ-регулятора для оси х, а затем у

         Уровень отклонений толщины проката при использовании многомерного ЛКГ-регулятора сопоставим с отклонениями, полученными для одномерных систем. Результаты, полученные при экспериментальном моделировании, иллюстрируют значительные преимущества прямого синтеза многомерных регуляторов.

1. Полухин П.И., Федосов Н.М. и др. Прокатное производство: Учебник для вузов, 3-е изд - М. Металлургия, 1982.
2. АСУ ТП современных балочных прокатных станов / Под ред. Б.Б. Тимофеева и В.И. Попельнуха. -М.Металлургия, 1984.
3. Файнберг Ю.М. Автоматизация непрерывных станов горячей прокатки - М.: Металлургия, 1963.
4. Солодовников В.В., Плотников В.Н., Яковлев А.В. Основы теории и элементы систем автоматического регулирования-М.: Машиностроение, 1985.
5. Медведев B.C., Потемкин В.Г. Control System Toolbox. Matlab 5 для студентов / Под ред. В.Г. Потемкина-М.: Диалог-МИФИ, 1999.