Оптимальный регулятор для управления приводами рельсобалочного прокатного стана

Выполнила:
Ст. гр. СУА-06м
Миргоязова А. В.

         Технологический процесс получения готового проката является завершающей стадией металлургического производства. Через прокатные цехи проходит почти вся сталь, выплавляемая в сталеплавильных цехах, поэтому наряду с увеличением производства проката существует проблема повышения эффективности прокатного производства и качества готового продукта.
         Актуальность системы управления прокатным станом состоит в том, что применяемые в настоящее время в промышленности регуляторы в большинстве случаев не обеспечивают оптимальных режимов работы.
         Прокатный стан предназначен для формирования профилей прямоугольного сечения из нагретых металлических заготовок - блюмов. Желаемая форма обеспечивается с помощью прокатных валков (рис.1).

Рисунок 1 - Формирование профиля прямоугольного сечения

         Целью управления приводами стана является обеспечение постоянства толщины проката по осям х и у в пределах заданных допусков. Отклонения в толщине профиля могут быть вызваны двумя причинами:

1. вариацией толщины и твердости заготовки;
2. наличием эксцентриситета прокатных валков.

         Для того чтобы уменьшить влияние этих возмущений, необходимо регулировать величину зазора за счет введения контура обратной связи. Поскольку зазор между валками измерить сложно, то вместо измерения толщины профиля измеряется сила нажатия валков.
         Как правило, физические системы, над которыми должно осуществляться управление, трудно рассматривать как детерминированные, поскольку наблюдениям доступны лишь искаженные шумом некоторые переменные их состояния. Таким образом, более реалистичными моделями таких систем в задачах управления являются модели, содержащие случайные процессы. При таких моделях требуется принимать решение или определять управление на основе результатов измерений, полученных в прошлом. В этом случае обе операции - оценивание состояния и управление - могут быть включены в единый процесс выбора решения. Линейно-квадратичная гауссовская задача является одним из частных случаев этой общей задачи оптимального управления.
         Для решения данной задачи задается математическая модель в виде системы уравнений:

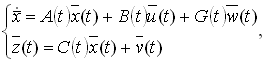                                                                            (1)

         Так как при управлении приводами прокатного стана необходимо обеспечить заданную точность толщины прокатываемого профиля, расходуя при этом минимум энергии, то автоматическая система управления будет оптимизироваться по точности и расходу энергии. Таким образом, критерий оптимальности для синтеза автоматического регулятора будет иметь вид:

                                                                            (2)

         где первое слагаемое критерия характеризует точность работы системы, а второе слагаемое - затраты энергии на управление.
         Q - симметричная, положительно полуопределенная матрица весовых коэффициентов размерности (n х n); R - симметричная положительно определенная матрица весовых коэффициентов размерности (m x m).
         Выбирая матрицы Q и R, можно получить компромиссное решение между точностью и быстродействием рассматриваемой динамической системы.
         Задача оптимизации состоит в том, чтобы найти совокупность векторов управляющих воздействий, обеспечивающих минимум критерия вида (2):

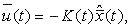                                                                                             (3)

         где - вектор оценки переменных состояния системы; K(t) - матрица коэффициентов оптимального управления размерности (m x n).
         В результате решения задачи синтеза регулятора на основе принципа максимума Понтрягина, получено уравнение Риккати:

                                                  (4)

         Решение матричного уравнения Риккати проведено в обратном направлении, от tf к t0. В результате полученного решения данного уравнения матрица К(t) алгоритма оптимального управления имеет вид:

                                                                            (5)

         На основании полученных в аналитической форме алгоритмов оптимального управления разработано прикладное программное обеспечение для автоматизации аналитического конструирования линейно-квадратичных регуляторов, применяемых при управлении приводами рельсобалочного прокатного стана. С целью улучшения качества управления произведен синтез многомерного регулятора для полной системы с учетом влияния перекрестных связей. Полученный регулятор по точности работы явно превосходит раздельные регуляторы по каждой оси. Результаты, полученные при экспериментальном моделировании, подтверждают правильность полученных алгоритмов синтеза линейно-квадратичных регуляторов и иллюстрируют значительные преимущества прямого синтеза многомерных регуляторов.

1. АСУ ТП современных балочных прокатных станов / Под ред. Б.Б. Тимофеева и В.И. Попельнуха. - М.Металлургия, 1984.
2. Файнберг Ю.М. Автоматизация непрерывных станов горячей прокатки - М.: Металлургия, 1963.
3. Медведев B.C., Потемкин В.Г. Control System Toolbox. Matlab 5 для студентов / Под ред. В.Г. Потемкина-М.: Диалог-МИФИ, 1999.