 Efficiently Solving Dynamic Markov Random Fields
using Graph Cuts
Efficiently Solving Dynamic Markov Random Fields
using Graph Cuts 
| Library | Abstract | Links | Report about the search | Individual task |
 Efficiently Solving Dynamic Markov Random Fields
using Graph Cuts
Efficiently Solving Dynamic Markov Random Fields
using Graph Cuts 
Pushmeet Kohli Philip H.S. Torr
Department of
Computing
Oxford Brookes
University
{fpushmeet.kohli,philiptorrg}@brookes.ac.uk
http://cms.brookes.ac.uk/computervision
Abstract
In this paper we present a fast new fully dynamic algorithm for the st-mincut/max-flow problem. We show how this algorithm can be used to efficiently compute MAP estimates for dynamically changing MRF models of labelling problems in computer vision, such as image segmentation. Specifically, given the solution of the max-flow problem on a graph, we show how to efficiently compute the maximum flow in a modified version of the graph. Our experiments showed that the time taken by our algorithm is roughly proportional to the number of edges whose weights were different in the two graphs. We test the performance of our algorithm on one particular problem: the object-background segmentation problem for video and compare it with the best known st-mincut algorithm. The results show that the dynamic graph cut algorithm is much faster than its static counterpart and enables real time image segmentation. It should be noted that our method is generic and can be used to yield similar improvements in many other cases that involve dynamic change in the graph.
1. Introduction
Graph cuts are being increasingly used in computer vision as an energy minimization technique. One of the primary reasons behind this growing popularity is the availability of numerous algorithms with excellent algorithmic complexity for solving the st-mincut problem [1]. Greig et al. [11] showed that the exact maximum a-posteriori (MAP) solution of a two label pairwise Markov Random Field (MRF) can be obtained in polynomial time by finding the st-mincut on the equivalent graph. This result has been extended by [12] for MRFs with multiple labels and convex priors. This equivalence between the st-mincut problem and MAP-MRF estimation makes graph cuts extremely important, especially considering the fact that the probability distributions of interacting labels of many problems such as image segmentation, stereo, image restoration can be modelled using MRFs. It has also been shown that a strong local optima of a MRF under the generalized Potts, and linear clique potential models can be obtained using graph cuts [5]. These are excellent results considering that the size of the state-space for the labelling problem is exponential in the number of nodes (sites) and the problem in general is NP-hard.
Given the solution to a MRF, the question arises as to whether this solution can help in solving another similar MRF with slightly different energy terms. For instance, this is the case when image segmentation is performed on the frames of a video where the data (image) in the problem changes from one time instance to the next. The MAP solution of the MRF representing the problem at the previous time instant should intuitively be a good initialization for the energy minimization procedure. If the change in the MRF is relatively small from one time instant to the next, such an initialization should substantially speed up the inference process since the time taken to find a new solution should be proportional to the change in the energy function. Within this paper we show that for the st-mincut/max-flow problem, this corresponds to the use of flows obtained in the solution of the previous problem instance in finding the solution to the next problem instance as seen in figure 1.

Figure 1: Dynamic image segmentation using Graph Cuts. The images in the first column are two consecutive frames of a video sequence and their respective segmentations, with the first image showing the user segmentation seeds (which are used as soft constraints on the segmentation). In column 2, we observe the n-edge flows obtained corresponding to the MAP solution of the MRFs representing the two problems. It can be clearly seen that the flows corresponding to the segmentations are similar. The flows from the first segmentation were used for finding the segmentation for the second frame. The time taken for this procedure was much less compared to that taken for finding the flows from scratch.
Such an algorithm for the max-flow problem would belong to a broad category of algorithms which are referred to as dynamic. These algorithms solve a problem by dynamically updating the solution of the previous problem instance. Their goal is to be more efficient than a recomputation of the problem solution after every change from scratch. Given a directed weighted graph, a fully dynamic algorithm should allow for unrestricted modification of the graph.
Graph Cuts in Computer vision We chose to incorporate dynamic information in graph cuts (over other inference algorithms like belief propagation) because of the fact that graph cuts provide exact global optimal solutions for certain energy functions. They have been used to obtain excellent results for a number of problems in computer vision and a thorough analysis of their applicability has been performed by researchers. Kolmogorov and Zabih [14] defined the set of energy functions which could be minimized using graph cuts by providing certain conditions which should be satisfied by all such functions. Boykov et al. [6] proposed algorithms based on graph cuts which could efficiently find approximate solutions to many different energy functions. A number of papers have also addressed the theoretical properties of graph constructions used in vision. These properties influence the efficiency of algorithms which solve the st-mincut problem. Boykov et al. [4] proposed a specialized algorithm for finding st-mincuts, which has been experimentally shown to be faster on graphs typically used in vision applications, compared to other algorithms for the problem.
Overview of Dynamic Graph Cuts Dynamic algorithms are not new to computer vision. They have been extensively used in computational geometry for problems such as range searching, intersections, point location, convex hull, proximity and many others. For more on dynamic algorithms used in computational geometry, the reader is referred to [7].
A number of algorithms have been proposed for the dynamic generalized mincut problem. Thorup [16] proposed a method which had a O(|E|1/2) update time and took O(log n) time per edge to list the cut edges. However, the dynamic st-mincut problem has remained relatively ignored until recently when Cohen and Tamassia [8] showed how dynamic expression trees can be used for maintaining st-mincuts in series-parallel diagraphs 1 with O(log m) time for update operations.
Boykov and Jolly [3] were the first to use a partially dynamic st-mincut algorithm in a vision application by proposing a technique with which they could update capacities of certain graph edges, and recompute the st-mincut dynamically. They used this method for performing interactive image segmentation, where the user could improve segmentation results by giving additional segmentation cues (seeds) in an online fashion. However, their scheme was restrictive and did not allow for changing the graph completely. We will explain this restriction in the context of dynamic MRFs later in the paper.
Organization of the Paper In this paper, we present a new fully dynamic algorithm for the st-mincut problem which allows for arbitrary changes in the graph. We show how this algorithm can be used to dynamically perform MAP inference in a MRF. Such an inference procedure is extremely fast and can be used in a number of problems.
Section 2 provides an overview of the st-mincut/maxflow problem. In section 3, we discuss MRFs and show how they are used to model labelling problems like image segmentation and stereo, and how MAP estimates for MRFs can be found using graph cuts. In section 4, we show how MAP solutions for dynamically changing MRFs can be efficiently computed by updating data structures used for solving the max-flow problem. Specifically, we describe how we transform the residual graph to reflect the changes in the original graph, and discuss issues related to the computational complexity of the dynamic algorithm. In section 5, we describe how the process of recomputing the st-mincut/max-flow can be further optimized by using recycled search trees. In section 6, we use the dynamic algorithm to perform image segmentation on video sequences, and compare its performance with that of the st-mincut algorithm described in [4].
2. Preliminaries
In this section we provide a general overview of the st-mincut/ maxflow problem, and give the notation used in the paper. A directed weighted graph G(V; E; C) with non-negative edge weights, is defined by a set of nodes V, a set of directed edges E, and an edge cost function C defined as:
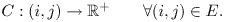 |
(1) |
Further, n and m denote the number of nodes |V| and the
number of edges |E| in the graph respectively. Graphs used
in the st-mincut problem have certain special nodes called
the terminal nodes, namely the source s, and the sink t. The
edges in the graph can be divided into two disjoint categories,
t-edges which connect a node to a terminal node, and n-edges
which connect nodes other than the terminal nodes with each
other. We make the following assumptions in our notation:
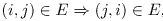 , and
, and 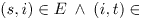 for all
for all
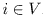 . These assumptions are non-restrictive as edges with
zero edge weights are allowed in our formulation. Thus we
can conform to our notation without changing the problem.
. These assumptions are non-restrictive as edges with
zero edge weights are allowed in our formulation. Thus we
can conform to our notation without changing the problem.
Definition 1 A cut is a partition of the node set V into two
parts S and 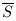 =V - S, and is defined by the set of edges
(i,j) such that i
=V - S, and is defined by the set of edges
(i,j) such that i  S and j
S and j 
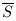 . The cost of the cut (S,
. The cost of the cut (S,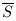 ) is
given as
) is
given as  . An st-cut is a cut satisfying
the properties s
. An st-cut is a cut satisfying
the properties s  S and t
S and t 
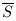 .
.
Given a directed weighted graph G, the st-mincut problem is that of finding a st-cut with the smallest cost. By the Ford-Fulkerson theorem [10], this is equivalent to computing the maximum flow from the source to the sink with the capacity of each edge equal to cij [1].
2.1. Formulating The Max-Flow Problem
For a network G(V; E) with a non-negative capacity cij associated with each edge, the max-flow problem is to find the maximum flow f from the source node s to the sink node t subject to the edge capacity and mass balance constraints:
 |
(2) | |
 |
(3) |
where fij is the flow from node i to node j, lij is the lower bound on the flow fij (which in our case is zero) and N(x) is the neighbourhood of x. Note here that we can initialize the flows in the t-edges as fsx=fxt=min(csx;cxt). This corresponds to pushing flow through the shortest augmenting path (defined later) from the source to the sink. The residual capacities of the terminal edges thus become:
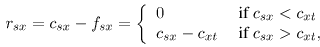 |
and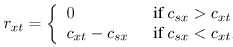 |
We observe here that the solution of the maximum flow problem is invariant to the absolute value of the terminal edge capacities csx and ctx. It only depends on the difference of these capacities (ctx - csx). Adding or subtracting a constant to these capacities changes the objective function by a constant and does not effect the overall solution. This property of the problem will be used later in the paper for updating the residual graph when the original graph has been modified.
2.2. Augmenting Paths and Residual Graphs
Given a flow fij, the residual capacity rij
of an edge (i; j)  E is the maximum additional flow that can be sent from node
i to node j using the edges (i; j) and (j; i). The residual
capacity rij has two components: the unused capacity of the
edge (i; j) : cij - fij, and the current flow fij from node j to
i which can be reduced to increase the flow from i to j.
E is the maximum additional flow that can be sent from node
i to node j using the edges (i; j) and (j; i). The residual
capacity rij has two components: the unused capacity of the
edge (i; j) : cij - fij, and the current flow fij from node j to
i which can be reduced to increase the flow from i to j.
Definition 2 A residual graph G(f) of a weighted graph G consists of the node set V and the edges with positive residual capacity (with respect to the flow f).
The topology of G(f) is identical to G. G(f) differs only in the capacity of its edges. For no flow i.e. f = {0}, G(f) is same as G.
Definition 3 An augmenting path is a path from the source to the sink along unsaturated edges of the residual graph.
Algorithms for solving the max-flow problem can be classified into two general categories: Augmenting Path and Preflow-push algorithms. Augmenting path algorithms repeatedly find augmenting paths in the residual graph G(f) and push the maximum possible flow f' through this path resulting in the total flow (f + f') and the residual graph G(f + f'). Preflow-push algorithms flood the network and create excess flow at the graph nodes. This excess flow is then incrementally drained out by sending it from the node toward the sink or the source.
3. Markov Random Fields
Consider a set of random variables X =
{ X1,X2,...,Xn} defined on the set S, such that, each variable
Xi can take a value xi from the set L ={ l1,l2,...,ln}
of all possible values. Then X is said to be a MRF with
respect to a neighborhood system N = { Ni| i  S} if and
only if it satisfies the positivity property P(x)>0, and
Markovian property P(xi|xS-{i}) = P(xi|xNi ),
S} if and
only if it satisfies the positivity property P(x)>0, and
Markovian property P(xi|xS-{i}) = P(xi|xNi ), 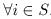 .
Here we refer to Pr(X = x) by P(x), Pr(Xi=xi) by
P(xi), and the joint event (X1 = x1,...,Xn = xn) as
X = x where x = { xi| i
.
Here we refer to Pr(X = x) by P(x), Pr(Xi=xi) by
P(xi), and the joint event (X1 = x1,...,Xn = xn) as
X = x where x = { xi| i  S} is a configuration of X
corresponding to a realization of the field.
S} is a configuration of X
corresponding to a realization of the field.
The MAP-MRF estimation can be formulated as an energy minimization problem where the energy corresponding to the configuration x is the negative log likelihood of the joint posterior probability of the MRF and is defined as
E(x)= - log Pr(x|D).
3.1. MRFs for Image Segmentation
In the context of image segmentation, S corresponds to the set of all image pixels, N is a neighbourhood defined on this set, the set L comprises of labels representing the different image segments, and the random variables in the set X denote the labelling of the pixels in the image. Note that every configuration x of the MRF defines a segmentation. The image segmentation problem can thus be solved by finding the least energy configuration of the MRF. The energy corresponding to a configuration x consists of a likelihood and a prior term as:
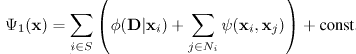 |
(5) |
where 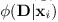 is the log likelihood which imposes individual penalties for assigning label li
to pixeli and is given by
is the log likelihood which imposes individual penalties for assigning label li
to pixeli and is given by
 if xi =lk if xi =lk |
(6) |
where Hk is the RGB distribution for Sk, the segment denoted
by label lk. Here, Pr( i  Sk | Hk )=Pr( Ii | Hk ),
where Ii is the colour intensity of the pixel i. The prior
Sk | Hk )=Pr( Ii | Hk ),
where Ii is the colour intensity of the pixel i. The prior 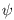 (xi,xj)
takes the form of a Generalized Potts model:
(xi,xj)
takes the form of a Generalized Potts model:
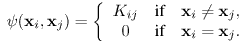 |
(7) |
In MRFs used for image segmentation, a contrast term is added which favours pixels with similar colour having the same label [2, 3, 15]. This is incorporated in the energy function by reducing the cost within the Potts model for two labels being different in proportion to the difference in intensities of their corresponding pixels. For instance, for the experiments mentioned in section 6, we use the term
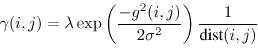 |
(8) |
where g2(i; j) measures the difference in the RGB values of pixels i and j and dist(i; j) gives the spatial distance between i and j. This term cannot be included in the prior, since the prior cannot include the data, and hence has to be added separately [15]. The energy function of the MRF now becomes
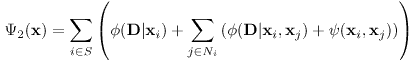 |
(9) |
The contrast term of the energy function is defined as
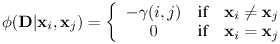 |
(10) |
3.2. Dynamic Markov Random Fields
Observe that the energy of the MRF defined earlier for image segmentation is dependent on the data (colour intensities of pixels) and the parameters used in the energy function. This also holds true for the MRF modelling the stereo labelling problem, where the label to be estimated for each MRF site (pixel) is the disparity configuration xp. When performing image segmentation on video sequences, the energy function of the MRF changes with every image frame. We refer to such a MRF as being dynamic. The stereo problem in the context of videos can be modelled using dynamic MRFs in a similar fashion [13]. The key contribution of this paper is the dynamic max-flow algorithm with which a solution of a dynamic MRF can be efficiently computed by using the solution of its previous state as shown in figure 1.
3.3. Solving MRFs using Graph Cuts
The configuration x of the MRF having the least energy corresponds
to the MAP solution of the MRF. The minimization of energies
such as the one defined in (9) can be performed
by computing graph cuts [5]. Further, a global minima
of the energy function can be computed exactly for a
pairwise MRF with convex pairwise terms by finding the st-mincut
on an equivalent graph [11, 12]. We now describe
the equivalent graph construction for the two label case, for
the multi-label case, the reader is referred to [12]. Each random
variable Xi of the MRF is represented by a vertex vi
in this graph, which is connected by n-edges to the vertices
in its neighbourhood set defined as { vk | Xk
 Ni }. The cost
of the n-edge (i; j) connecting vertices vi and vj is given by
Ni }. The cost
of the n-edge (i; j) connecting vertices vi and vj is given by
 .
.
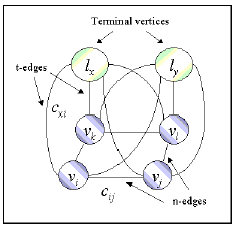
Figure 2: The graph representing an MRF with two labels lx and ly,
and four random variables xi, xj, xk, and xl.
The cost of the t-edge cxi is  and the n-edge cij is
and the n-edge cij is
 .
.
The two labels lx and ly are represented by the special vertices,
the source s and the sink t. They are connected to all
other vertices representing the latent variables in the MRF by
t-edges. The cost of a t-edge is given by the likelihood term
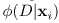 of the energy function of the MRF. An st-cut in this
graph which separates the source and the sink, defines a configuration
x of the MRF, and the cost of the cut is the energy
of x [5]. From this equivalence, by computing the minimum
cost cut we can find the MAP-solution of the MRF.
of the energy function of the MRF. An st-cut in this
graph which separates the source and the sink, defines a configuration
x of the MRF, and the cost of the cut is the energy
of x [5]. From this equivalence, by computing the minimum
cost cut we can find the MAP-solution of the MRF.
4. Estimating MAP solutions for Dynamic MRFs
We now come to the main contribution of the paper. Having shown how any energy function defining a pairwise MRF can be minimized exactly by solving a st-mincut/maxflow problem, we now show how this solution can be used to efficiently solve any similar energy function. Consider two MRFs Ma and Mb whose corresponding energy functions Ea and Eb differ by a few terms. Suppose we have found the MAP solution of Ma by solving the max-flow problem on the graph Ga representing the energy Ea and now want to find the solution of Mb. Note that the graph representing Eb i.e. Gb differs from Ga by a few edge costs. Instead of recomputing the max-flow on Gb from scratch, we dynamically update the flows obtained while solving Ea by incorporating the differences between Ga and Gb in the residual graph obtained from the max-flow solution of Ga. In this process we are able to preserve the flow from the source to the sink which is not affected by the differences in the edge capacities(costs) of Ga and Gb. After updating the flows and residual edge capacities, the max-flow algorithm is restarted on the residual graph.
Boykov and Jolly [3] in their work on interactive image segmentation, used this technique for efficiently recomputing the MAP solution when the likelihood term (6) changes (due to addition of new hard and soft constraints by the user). However, their technique was restrictive and could only handle changes in the cost of t-edges of the graph. Our new method can handle arbitrary changes in the graph. In our experiments, we used this approach to efficiently recompute the MAP solution for the image segmentation problem in videos. Note that a change of image, results in changes in both the likelihood and contrast terms of the energy function.
4.1. Updating Residual Graphs
While modifying the residual graph, certain flows may violate the new edge capacity constraints. We now show how the residual graph is transformed to make such flows consistent. We address the problem of updating edge capacities for n-edges and t-edges separately.
4.1.1 Modifying n-edge Capacities
We now discuss how we update the residual graph when n-edge capacities are changed. The reader should note here that this case was not addressed in [3]. We use c'i,j to refer to the new edge capacity, and r'i,j and f'i,j to represent the updated residual capacity and flow respectively for the edge (i; j). Observe that updating edge capacities in the residual graph is trivial if the new edge capacity c'i,j is greater than or equal to the old edge capacity c'i,j. The updated residual capacity r'i,j is obtained as:
| r'i,j =ri,j + (c'i,j - ci,j ) | (11) |
Even if c'i,j is less than ci,j , the procedure still remains trivial if the flow fi,j is less than the new edge capacity c'i,j . This is due to the fact that the reduction in the edge capacity does not affect the flow consistency of the network i.e. flow fi,j satisfies the edge capacity constraint (2) for the new edge capacity. The residual capacity of the edge can still be updated according to equation (11). The difference in this case is that (c'i,j - ci,j ) is negative and hence will result in the reduction of the residual capacity. In both these cases, the flow through the edge remains unchanged i.e. (f'i,j = fi,j ).
The problem ceases to remain trivial in the case when the new edge capacity c'i,j is less than the flow fi,j. In this case, fi,j violates the edge capacity constraint (2). To make fi,j consistent, we have to retract the excess flow (fi,j - c'i,j ) from the edge (i; j). At this point, the reader should note that a trivial solution for this operation would be to push back the flow through the augmenting path it originally came through. However such an operation would be extremely computationally expensive.
We now show how we resolve this inconsistency in constant i.e. O(1) time. We set the value of the edge flow equal to the new edge capacity i.e.f'i,j =c'i,j. This change in the flow value changes the residual capacities of the edges (i; j) and (i; j) as: ri,j =c'i,j - f'i,j = 0 and r'i,j =ci,j + f'i,j. Further, this change in the flow through edge (i; j) creates a surplus si of flow at node i and a deficiency dj of flow at node j, which violate the mass balance constraints(3) for node i and node j where si = dj = fi,j - f'i,j = fi,j - c'i,j
Satisfying the Mass Balance Constraints The mass balance constraint for node i after updating the flows becomes
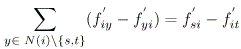 |
(12) |
Keeping flow of all n-edges other than the edge (i; j) the same i.e.
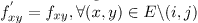 and subtracting equation (12) from (3), we get
f'si =f'it= fsi-fit-si.
Setting f'si= fsi, it becomes
f'it= fit+si.
Similarly, for node j, we get f'sj= fsj+dj.
and subtracting equation (12) from (3), we get
f'si =f'it= fsi-fit-si.
Setting f'si= fsi, it becomes
f'it= fit+si.
Similarly, for node j, we get f'sj= fsj+dj.
We now focus on the mass balance constraint of node i
(for node j, the process will be similar). The new value
of the flow from node i to the sink node t,f'it
it satisfies the mass balance constraint for node i and in effect solves our
problem. However, a problem arises if this new value of
flow violates the edge capacity constraints for the edge (i; t)
i.e. f'it >cit.
To overcome this problem we add a constant  to the capacities of both the edges (i; t) and (s; i)
to get c'it and c'si
respectively where
to the capacities of both the edges (i; t) and (s; i)
to get c'it and c'si
respectively where  = max {0, f'it - cit },
or
= max {0, f'it - cit },
or  = max {0, (fit + si) - cit },
or
= max {0, (fit + si) - cit },
or  = max {0, si - rit }.
This transformation changes the objective function value by
a constant and hence, does not change the optimal solution.
This constant can be recorded separately and ignored while
solving the problem. The residual capacities of these edges
now become
= max {0, si - rit }.
This transformation changes the objective function value by
a constant and hence, does not change the optimal solution.
This constant can be recorded separately and ignored while
solving the problem. The residual capacities of these edges
now become
r'si =(csi +  ) -
f'si ) -
f'si |
(13) |
and
r'it =(cit +  ) -
f'it ) -
f'it |
(14) |
On substituting  in (13,14) and simplifying, we get:
in (13,14) and simplifying, we get:
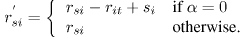
and
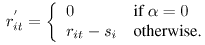
Similarly, for node j, we get:

and
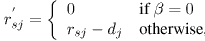
where 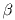 =
max{0, f'sj - csj }.
The steps to update the residual graph, in the case when the updated edge capacity
c'ij is less than the flow fij are shown in figure 3.
=
max{0, f'sj - csj }.
The steps to update the residual graph, in the case when the updated edge capacity
c'ij is less than the flow fij are shown in figure 3.
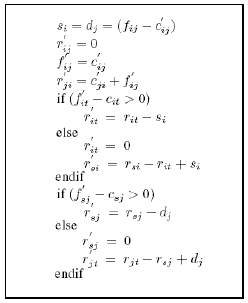
Figure 3: Pseudocode to update the residual graph when the updated edge capacity c'ij is less than the flow fij.
4.1.2 Modifying t-edge Capacities
Our method for updating terminal edges is similar to the one
used in [3]. We skip the trivial cases where the flow fsi is
less than the updated edge capacity c'si, and directly address
the case where the flow is greater than the updated edge capacity
and hence violates the edge capacity constraint (2).
To make the flow consistent, a constant  =fsi - c'si is
added to both the t -edges connected to the node i. Such a
change does not affect the solution of the st-mincut problem
as explained earlier. The residual capacities thus become:
r'si = c'si - fsi +
=fsi - c'si is
added to both the t -edges connected to the node i. Such a
change does not affect the solution of the st-mincut problem
as explained earlier. The residual capacities thus become:
r'si = c'si - fsi +  = 0
and r'it = cit - fit +
= 0
and r'it = cit - fit +  ,
or r'it = rit - c'si + fsi.
,
or r'it = rit - c'si + fsi.
4.2. Complexity Analysis of Update Operations
Modifying an edge cost in the residual graph takes constant time. Arbitrary changes in the graph like addition or deletion of nodes and edges can be expressed in terms of modifying an edge cost. The time complexity of all such changes is O(1) except for deleting a node, where the update time is O(k ), where k is degree of the node to be deleted.
After the residual graph has been updated to reflect the changes in the MRF, the generic augmenting path procedure is started to find the maximum flow. This involves repeatedly finding augmenting paths in the residual graph and saturating them. When no more augmenting paths can be found i.e. the source and sink are disconnected in the residual graph, we reach the maximum flow.
The maximum flow from the source to the sink is a loose
upper bound on the number of augmenting paths founds by
the augmenting path procedure. Also, the total change in
edge capacity bounds the increase in the flow 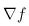 defined as:
defined as:
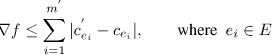 |
or, 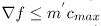 where
cmax = max( |c'ei-cei| ).
Thus we get a trivial O(m 'cmax ) bound on the number of augmentations,
where m ' is the number of edge capacity updates.
where
cmax = max( |c'ei-cei| ).
Thus we get a trivial O(m 'cmax ) bound on the number of augmentations,
where m ' is the number of edge capacity updates.
5. Optimizing the Algorithm
We have already seen how by dynamically updating the residual graph, we can reduce the time taken to compute the st-mincut. We can further improve the running time by using a technique motivated by the augmenting path based algorithm proposed in [4] for solving the st-mincut/max-flow problem. Typical augmenting path based methods start a new breadth-first search for (source to sink) paths as soon as all paths of a given length are exhausted. For instance, Dinic [9] proposed an augmenting path algorithm which builds search trees to find augmenting paths. This is a computationally expensive operation, as it involves visiting almost all nodes of the graph, and makes the algorithm slow if it has to be performed too often. To counter this, Boykov et al. [4] proposed an algorithm in which they re-used the search tree. In their experiments, this new algorithm outperformed the best-known augmenting-path and push-relabel algorithms on graphs commonly used in computer vision.
In our dynamic max-flow algorithm, we reuse the search tree available from the previous max-flow computation to find the solution in the updated residual graph. This technique saves us the cost of creating a new search tree, thus making our algorithm substantially faster. We next describe how the algorithm in [4] works and how we recycle the search trees and use them.
5.1. Reusing Search Trees
The algorithm maintains two non-overlapping search trees S and T with roots at the source s and the sink t respectively. In tree S all edges from each parent node to its children are non-saturated, while in tree T edges from children to their parents are non-saturated. The nodes that are not in S or T are called free. The nodes in the search trees S and T can be either active (can grow by acquiring new children along non-saturated edges) or passive. When an active node comes in contact with a node from the other tree, an augmenting path is found. The algorithm has three basic stages:
Growth Stage: The search trees S and T are grown until they touch resulting in an augmenting path. The active nodes explore adjacent non-saturated edges and acquire new children from the set of free nodes, which now become active. As soon as all neighbours of a given active node are explored the active node becomes passive.
Augmentation Stage: Flow is pushed through the path found in the growth stage. This results in some nodes of the trees S and T becoming orphans since the edges linking them to their parents become saturated. Note that this breaks the source and sink search trees into forests.
Adoption Stage: The search trees are then restored by finding a new valid parent (of the same set, through a non-saturated edge) for each orphan. If no qualifying parent can be found, the node is made free.
While dynamically updating the residual graph, certain edges of the trees S and T may become saturated. These edges have to be deleted breaking the trees into forests and making certain nodes orphans. We keep track of all the orphaned nodes and before recomputing the st-mincut on the modified residual graph, restore the trees by finding a new valid parent for every node.
6. Experimental Analysis
We now demonstrate the performance of our method using the object-background segmentation problem. Note that although we illustrate our algorithm on the video segmentation problem for ease of demonstration, our new algorithm can be used to efficiently find exact solutions of general dynamic pairwise MRFs with convex priors.
6.1. Fast Image Segmentation in Videos
The object-background segmentation problem aims to cut out the objects in an image so that they can be pasted in a different context [3]. In our case, this process has to be performed over all frames in the video sequence. The problem is formulated as follows.
The user specifies hard and soft constraints on the segmentation
by providing segmentation cues or seeds. The soft
constraints are used to build colour histograms for the object
and background, which are used for calculating the likelihood
term  of the energy function (9) of the MRF
[3]. The hard constraints consists of strict pixel label values
which have to be maintained through all the frames of the
video. These constraints are used for specifying pixel positions
which are guaranteed to have the same label (object or
background) throughout the video sequence and do not contribute
to the colour histograms.
of the energy function (9) of the MRF
[3]. The hard constraints consists of strict pixel label values
which have to be maintained through all the frames of the
video. These constraints are used for specifying pixel positions
which are guaranteed to have the same label (object or
background) throughout the video sequence and do not contribute
to the colour histograms.
We impose the hard constraints on the segmentation by
incorporating them in the likelihood term  . This is
done by imposing a very high cost for a label assignment
that violates the hard constraints. Figure 4 demonstrates the
use of constraints in the image segmentation process. The
segmentation results are shown in figure 5.
. This is
done by imposing a very high cost for a label assignment
that violates the hard constraints. Figure 4 demonstrates the
use of constraints in the image segmentation process. The
segmentation results are shown in figure 5.

Figure 4: Segmentation using user constraints. The first image is the input showing the soft constraints (as in [3]) represented by black (background) and white (foreground) rectangles. The second image shows the segmentation obtained using the soft constraints, which contains a certain portion of the background wrongly marked as the foreground due to similar colour intensity. The third image is the segmentation result obtained by using a hard constraint on the area along with the soft constraints.

Figure 5: Segmentation results of the human lame walk video sequence.
6.2. Performance Evaluation
We tested the dynamic graph cut algorithm on a number of video sequences and compared its performance with the dual-search tree algorithm proposed in [4], which has been experimentally shown to be the fastest for several vision problems including image segmentation. We refer this algorithm as static since it starts afresh for each problem instance.
The video sequences used in our tests had between one hundred to a thousand image frames. For all the video sequences, dynamically updating the residual graph produced a substantial decrease in the number of augmenting paths. Further, the dynamic algorithms (normal and optimized) were substantially faster than the static algorithm. The exact speed-up as expected was observed to be dependent on the amount change in the MRF. A 5-10 time speed-up was observed on high frame rate sequences. The average running times per image frame for the static, dynamic and optimized-dynamic algorithms for the human lame walk sequence 7 of size (368x256) were 91.4, 66.0, and 33.6 milliseconds and for the grazing cow sequence of size (720x578) were 188.8, 151.3, and 78.0 milliseconds respectively. The time taken by the dynamic algorithm includes the time taken to recycle the search trees. The experiments were performed on a Pentium 4 2.8 GHz machine.
7. Conclusion
In this paper, we have presented a new fully dynamic algorithm for the st-mincut problem which can be used to find exact MAP solutions for dynamically changing MRFs rapidly. It should be noted that our method is generic and finds exact solutions for all dynamic problems which can be modelled as pairwise MRFs with convex priors. The results show that our algorithm is substantially faster than the best-known st-mincut algorithm, which recomputes the solution from the start. We have demonstrated how this method can be used to perform real-time image segmentation in video sequences.
References
[1] R. Ahuja, T. Magnanti, and J. Orlin. Network Flows. Prentice
Hall, Eaglewood Cliffs, NJ, 1993.
[2] A. Blake, C. Rother, M. Brown, P. Perez, and P. Torr. Interac-tive
image segmentation using an adaptive gmmrf model. In
ECCV04, pages Vol I: 428–441, 2004.
[3] Y. Boykov and M. Jolly. Interactive graph cuts for optimal
boundary and region segmentation of objects in n-d images.
In ICCV, pages I: 105–112, 2001.
[4] Y. Boykov and V. Kolmogorov. An experimental comparison
of min-cut/max-flow algorithms for energy minimization in
vision. PAMI, 26(9):1124–1137, September 2004.
[5] Y. Boykov, O. Veksler, and R. Zabih. Markov random fields
with efficient approximations. In CVPR, pages 648–655,
1998.
[6] Y. Boykov, O. Veksler, and R. Zabih. Fast approximate en-ergy
minimization via graph cuts. In ICCV, pages I: 377–384,
1999.
[7] Y.-J. Chiang and R. Tamassia. Dynamic algorithms in com-putational
geometry. Technical Report CS-91-24, 1991.
[8] R. F. Cohen and R. Tamassia. Dynamic expression trees and
their applications. In SODA, pages 52–61, 1991.
[9] E. A. Dinic. Algorithm for solution of a problem of maximum
flow in networks with power estimation. Soviet Math. Dokl.,
11:1277–1280, 1970.
[10] L. Ford and D. Fulkerson. Flows in Networks. Princeton
University Press, Princeton, 1962.
[11] D. Greig, B. Porteous, and A. Seheult. Exact maximum a pos-teriori
estimation for binary images. RoyalStat, B: 51(2):271–
279, 1989.
[12] H. Ishikawa. Exact optimization for markov random fields
with convex priors. PAMI, 25(10):1333–1336, October 2003.
[13] P. Kohli and P. H. S. Torr. Dynamic energy minimization for
stereo. In preparation, 2005.
[14] V. Kolmogorov and R. Zabih. What energy functions can be
minimized via graph cuts? In ECCV02, page III: 65 ff., 2002.
[15] M. P. Kumar, P. H. S. Torr, and A. Zisserman. Obj cut. In
CVPR05, pages 18–5, 2005.
[16] M. Thorup. Fully-dynamic min-cut. In STOC, pages 224–
230, 2001.


| Library | Abstract | Links | Report about the search | Individual task |