 ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ ИЗОБРАЖЕНИЙ
НА ОСНОВАНИИ
ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ ИЗОБРАЖЕНИЙ
НА ОСНОВАНИИ 
МАРКОВСКИХ СЛУЧАЙНЫХ ПОЛЕЙ
| Библиотека | Реферат | Ссылки | Отчет о поиске | Индивидуальное задание |
 ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ ИЗОБРАЖЕНИЙ
НА ОСНОВАНИИ
ТЕКСТУРНАЯ СЕГМЕНТАЦИЯ ИЗОБРАЖЕНИЙ
НА ОСНОВАНИИ 
МАРКОВСКИХ СЛУЧАЙНЫХ ПОЛЕЙ
И.В. Ковтун
Первоисточник: http://irtc.org.ua/image/Files/kovtun/kovtun_usim_2003(4)_rus.pdf
В данной статье вводится модель изображения, состоящего из нескольких текстур. Особенность введенной модели состоит в том, что сегментация и каждая текстура задаются независимыми марковскими случайными полями. Данная модель позволяет избежать каких-либо дополнительных ограничений на рассматриваемые марковские случайные поля, таких, как авторегрессионность или гауссовость. Также рассматриваются возможные постановки задач сегментации, основанные на указанной модели, и исследуются возможности их решения.
Текстурна сегментація зображень на основі марковських випадкових полів
Ковтун І.В.
В даній статті вводиться модель зображення, яке складається з кількох текстур. Особливість введеної моделі полягає в тому, що сегментація і кожна текстура задаються незалежними марковськими випадковими полями. Дана модель дозволяє уникнути яких-небудь додаткових обмежень, таких, як авторегресійність або гауссовість, на марковські випадкові поля, що розглядаються. Також розглядаються можливі постановки задач сегментації, основані на вказаній моделі, і досліджуються можливі їх розв ’язки.
Texture Segmentation of Images on the basis of Markov Random Fields
Kovtun I.V.
This paper presents a new model of the textured image consisting of several textures. The segmentation and each texture are described by their own Markov random fields. Such model allows to avoid any additional restrictions on the random fields, such as autoregressivness or gaussianity. Different segmentation problem formulations based on this model and solutions to them are considered as well.
Текстурная сегментация изображений на основании марковских случайных полей
Ковтун І.В.
1. Введение
Текстуры являются важной характеристикой изображений естественных объектов и важным элементом зрительного восприятия. Машинному анализу текстурных изображений посвящено значительное количество исследований [1]. В круге этих исследований существенную часть занимает проблема сегментации изображений по текстурным признакам. В многолетних исследованиях этой проблемы можно выделить следующие три основные группы.
1. В первую группу работ мы включаем обширные исследования, выполненные в этой области до опубликования основополагающей работы Джименов [2]. Эти исследования характеризуются тем, что на основании определенных разумных или интуитивных, эвристических соображений постулируются те или иные текстурные признаки, вычисляемые для каждого пиксела на основании некоторой окрестности этого пиксела. Поэтому эти алгоритмы еще называются windows-like алгоритмами. Алгоритмы текстурной сегментации конструируются не как решение формально поставленных задач, а на неформальных соображениях. Предполагается, что текстурный признак внутри одного сегмента меняется не слишком сильно, а на разных сегментах принимает существенно различные значения. Достаточно часто алгоритмы этого класса принимают вид известных под названием "наращивание " или "слияние " областей. Весьма распространены алгоритмы, в которых на основании выбранных признаков выделяются контуры, то есть границы между двумя сегментами, а затем тем или иным способом строятся области в соответствии с выделенными границами. Эвристические работы такого характера выполнялись как до работы Джименов [2], так и после нее. Относя эти работы к доджименовскому периоду, мы хотим подчеркнуть основополагающее значение работ Джименов, в которых задача текстурной сегментации получила четкую математическую формулировку.
2. В работе Джименов задача текстурной сегментации сформулирована на основе марковских моделей изображения и состоит в поиске реализации скрытого марковского поля с наибольшей апостериорной вероятностью. Эта задача сводится к оптимизационным задачам чрезвычайной сложности, за исключением некоторых частных случаев, когда, например, марковское поле является авторегрессионным или гауссовым. Для решения общей задачи предложен метод моделируемого отжига (simulated annealing), который до этого успешно применялся для практического решения других теоретически безнадежных задач [3,4]. По-видимому, именно после работы Джименов метод моделируемого отжига стал широко применятся в обработке и распознавании изображений. Известно, однако, что моделируемый отжиг не определяет однозначно алгоритм отыскания глобального оптимума, а лишь указывает, что искомый алгоритм принадлежит обширному классу алгоритмов, отличающихся друг от друга процессом изменения специального параметра- так называемой "температуры " отжига. Только при определенной зависимости этой температуры от времени алгоритмы моделируемого отжига обеспечивают сходимость к глобальному максимуму оптимизируемой функции. Выбор зависимости температуры от времени составлял основную проблему при использовании рекомендаций Джименов при решении практических задач.
3. Дальнейший прогресс в задачах текстурной сегментации определили результаты в области структурного распознавания, исследованного с точки зрения Байесовской теории статистических решений [5,6,7]. Стало известно, что отыскание сегментации с наибольшей апостериорной вероятностью является решением лишь одной из нескольких возможных байесовских задач распознавания. Более того, в ряде приложений такое решение является просто неразумным, что следует из функции потерь, которая в этом случае является совершенно неестественной. Эти результаты дали возможность построения новых алгоритмов распознавания скрытых марковских полей [8,9,10,11,12]. По своему характеру эти алгоритмы весьма близки к алгоритмам стохастической релаксации Джименов, но при этом оказалось ненужным решать трудную и до сих пор нерешенную проблему о скорости уменьшения "температуры ". Задачи распознавания скрытых марковских полей, в частности, текстурной сегментации изображений оказались погруженными в более общую проблему моделирования и генерирования марковских случайных полей. В этом круге исследований проблема собственно сегментации изображений потеряла свою специфику.
В данной работе делается попытка выделить проблему текстурной сегментации из общего класса задач генерирования и моделирования марковских случайных полей. Мы построим алгоритмы текстурной сегментации, которые учитывают специфику этого подкласса задач в общей задаче генерирования марковских случайных полей. Эти алгоритмы будут построены не на основании общей марковской модели изображений, а на основании модели именно таких изображений, которые составлены из нескольких сегментов, каждый из которых является случайной реализацией марковского случайного поля, своего для каждого сегмента.
В следующих двух разделах, втором и третьем, даются базовые определения, необходимые для точной формулировки задачи. В четвертом разделе вводится модель изображения, состоящего из нескольких текстур. В пятом разделе приводятся возможные постановки задач текстурной сегментации в рамках байесовской теории распознавания. В шестом разделе предлагается метод сведения этих задач к задачам генерирования марковских случайных полей. В седьмом разделе описан алгоритм генерирования марковского случайного поля для сформулированной модели текстурного изображения. В восьмом разделе приведены примеры практической реализации предложенного алгоритма.
2. Основные определения
В данном разделе мы введем базовые определения. Нам в дальнейшем понадобится оперировать такими понятиями, как поле зрения, пиксел, палитра, цвет, изображение, разметка, метка, структура поля зрения. Большинство из этих понятий являются "интуитивно понятными ", но все же мы введем их для определенности.
Полем зрения будем называть произвольное конечное множество. В дальнейшем будем обозначать его символом T. Элементы поля зрения назовем пикселами. Одним из наиболее часто встречающихся примеров поля зрения является прямоугольный участок двумерной целочисленной решетки {(i,j) | 0<= i < I, 0<= j < J }. Без ограничений общности можно считать, что элементами поля зрения являются натуральные числа T={1,2,...,n}.
Палитрой, так же, как и полем зрения, будем называть произвольное конечное множество. В данной статье палитра обозначается символом X. Элементы палитры X будем называть цветами. Без ограничения общности можно считать, что X={1,2,...,n}.
Изображением на поле зрения T с палитрой X будем называть функцию: xT : T 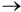 X,
которая каждому пикселу поля зрения ставит в соответствие какой-то цвет из палитры. Сужение этой функции
на подмножество поля зрения
X,
которая каждому пикселу поля зрения ставит в соответствие какой-то цвет из палитры. Сужение этой функции
на подмножество поля зрения 
 T
будем обозначать x
T
будем обозначать x , а значение функции xT в пикселе
t
, а значение функции xT в пикселе
t 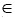 T обозначим xt.
T обозначим xt.
Разметкой поля зрения T на l сегментов будем называть функцию kT : T 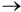 {1,2,...,l}.
При этом множество {1,2,...,l} назовем множеством меток и обозначим символом K.
Последние два определения почти идентичны. Необходимость введения двух определений
вместо одного обусловлена тем, что понятия «изображение » и «разметка » несут разную смысловую
нагрузку, и поэтому их разделение улучшает понимание изложенного материала. С теоретической же
точки зрения разметка ничем не отличается от изображения.
{1,2,...,l}.
При этом множество {1,2,...,l} назовем множеством меток и обозначим символом K.
Последние два определения почти идентичны. Необходимость введения двух определений
вместо одного обусловлена тем, что понятия «изображение » и «разметка » несут разную смысловую
нагрузку, и поэтому их разделение улучшает понимание изложенного материала. С теоретической же
точки зрения разметка ничем не отличается от изображения.
Структурой поля зрения T назовем семейство подмножеств 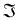 этого поля зрения
этого поля зрения
 .
.
Отметим, что множество 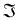 не обязано содержать в себе все подмножества поля зрения. Обычно,
но совсем не обязательно, элементы структуры поля зрения состоят не более чем из двух пикселов.
не обязано содержать в себе все подмножества поля зрения. Обычно,
но совсем не обязательно, элементы структуры поля зрения состоят не более чем из двух пикселов.
3. Понятие случайного поля, марковское случайное поле
Если на множестве всех изображений xT ={xT | xT : T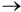 X}
задана случайная величина N, то эту случайную величину называют случайным полем. Поскольку задать непосредственно
распределение вероятностей на множестве всех изображений в силу их огромного количества
невозможно, то случайное поле N рассматривается обычно как семейство случайных величин
N={N1 | t
X}
задана случайная величина N, то эту случайную величину называют случайным полем. Поскольку задать непосредственно
распределение вероятностей на множестве всех изображений в силу их огромного количества
невозможно, то случайное поле N рассматривается обычно как семейство случайных величин
N={N1 | t 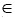 T} = {N1 , N2 ,...,Nm }.
Каждая случайная величина Nt соответствует одному пикселу t. Ее
множество значений равно X. При этом случайные величины N1 , N2 ,...,Nm
не обязаны быть независимыми друг от друга. Для заданного изображения:
xT : T
T} = {N1 , N2 ,...,Nm }.
Каждая случайная величина Nt соответствует одному пикселу t. Ее
множество значений равно X. При этом случайные величины N1 , N2 ,...,Nm
не обязаны быть независимыми друг от друга. Для заданного изображения:
xT : T 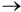 X через
p(xT ) обозначим вероятность события
(x1 =N1 , x2 =N2 ,...,xm =Nm).
Для подмножества пикселей
X через
p(xT ) обозначим вероятность события
(x1 =N1 , x2 =N2 ,...,xm =Nm).
Для подмножества пикселей  поля зрения T через
p(x
поля зрения T через
p(x ) обозначим вероятность события
{xt =Nt | t
) обозначим вероятность события
{xt =Nt | t 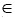
 }.
}.
В данной работе все случайные поля предполагаются марковскими, то есть такими, распределение вероятностей которых имеет вид:
 |
(1) |
где  - нормирующий множитель,
- нормирующий множитель, 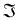 - структура поля зрения,
- структура поля зрения,
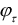 - функции, зависящие от переменных
{x
- функции, зависящие от переменных
{x ={xt | t
={xt | t 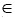
 }.
Функции
}.
Функции 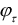 называются Гиббсовскими потенциалами.
называются Гиббсовскими потенциалами.
В работах [8,9,10,11] показано, что марковские случайные поля могут быть использованы для описания текстур. Кроме того, известен алгоритм генерирования марковского случайного поля в соответствии с распределением вероятностей (1). Этот алгоритм основан на том факте, что распределение вероятностей метки в одном пикселе при фиксированных метках во всех остальных пикселах легко вычисляется:
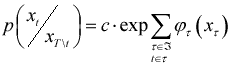 |
(2) |
где  - нормирующий множитель, обеспечивающий равенство
- нормирующий множитель, обеспечивающий равенство
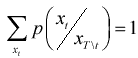 .
.
Сам же алгоритм генерирования заключается в следующем. На первом шаге алгоритма
выбирается произвольное изображение xT. Далее многократно повторяется следующая операция:
выбирается произвольный пиксел поля зрения t 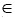 T, цвет в котором изменяется. Цвет в этом пикселе
генерируется в соответствии с распределением вероятностей (2).
T, цвет в котором изменяется. Цвет в этом пикселе
генерируется в соответствии с распределением вероятностей (2).
4. Введение базовой модели текстурного изображения, содержащего l текстур
Пусть на множестве всех изображений
xT задано l случайных полей. Распределения
вероятностей этих случайных полей будем обозначать
p1(xT ), p2(xT ),...,pl(xT ) соответственно.
Каждое из этих случайных полей соответствует определенному типу текстуры. Верхние индексы
обозначают номера текстур. Пусть также задано одно случайное поле на множестве всех разметок поля
зрения T на l сегментов. Вероятность разметки: kt: T 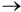 K
обозначим через pразм(kt).
K
обозначим через pразм(kt).
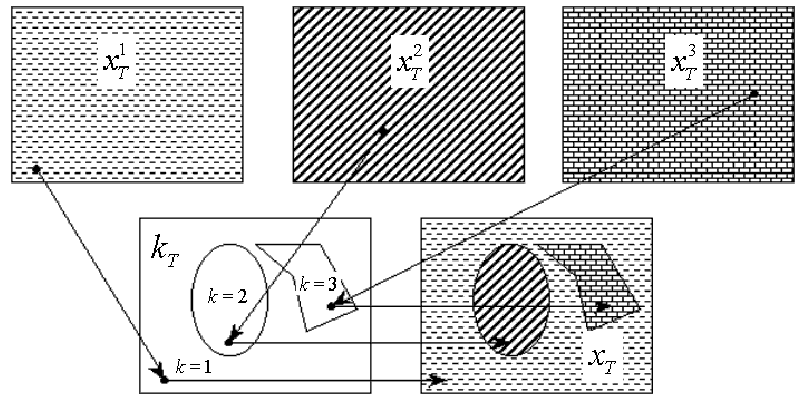
Рис. 1. Общая модель текстурного изображения, построенного согласно формуле (3).
Текстурным изображением xT назовем изображение, полученное в результате следующего
случайного процесса. Независимо друг от друга генерируются l изображений
x1T,x2T,...,xlT
и разметка kT в соответствии с распределениями
p1(xT),p2(xT),...,pl(xT)
и pразм(kt) соответственно. Далее
текстурное изображение xT строится из полученных изображений согласно следующему правилу: если
пиксел t разметки имеет метку kt 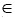 K= {1,2,...,l},
то в соответствующий пиксел xt результирующего
изображения переносится цвет из изображения k-той текстуры
xkT (см. рис. 1). Точнее, цвет xt каждого
пиксела t
K= {1,2,...,l},
то в соответствующий пиксел xt результирующего
изображения переносится цвет из изображения k-той текстуры
xkT (см. рис. 1). Точнее, цвет xt каждого
пиксела t 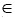 T вычисляется по формуле
T вычисляется по формуле
 |
(3) |
Из построения следует формула для совместного распределения вероятностей изображений x1T,x2T,...,xlT, kT и xT:
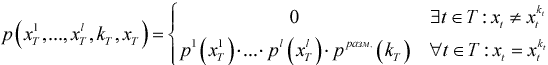 |
(4) |
Исходя из описанной модели требуется по известному изображению xT "восстановить " разметку kT.
В качестве модели случайного поля выберем марковское поле. Модель текстурного изображения будет описываться l+1 структурой поля зрения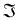 1,
1,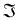 2,
...,
2,
...,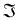 l,
l,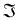 разм
и для любого i
разм
и для любого i 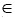 {1,2,..,l,разм}, для
любого
{1,2,..,l,разм}, для
любого 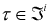 функции
функции 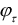 задают гиббсовские потенциалы. Распределение вероятностей изображения
текстуры xiT задается формулой
задают гиббсовские потенциалы. Распределение вероятностей изображения
текстуры xiT задается формулой 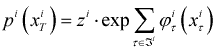 , а распределение вероятностей
разметки kT равно
, а распределение вероятностей
разметки kT равно 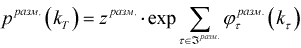 .
.
В работах Г.Л.Гимельфарба [8,9,10] и А.Залесного [10,11] предлагается рассматривать текстурную сегментацию изображений, как частный случай генерирования марковских случайных полей. При этом цвет каждого пиксела состоит из двух компонент (x,k)- цвета и метки. При этом неявно предполагается, что структура поля зрения для различных текстур совпадает. Преимущество введенной только что модели состоит в том, что разметка и каждая текстура характеризуется своими марковскими случайными полями, не зависящими друг от друга. Это позволит легко модифицировать распознающую систему. Введение новой текстуры или удаление существующей происходит в рамках введенной модели очень просто. Кроме того, в данной модели легко учитываются априорные знания о разметке.
5. Формулировка задач сегментации как байесовских задач распознавания
Зная совместное распределение вероятностей p(x1T,x2T,...,xlT, kT,xT) и изображение xT требуется найти разметку kT. Рассмотрим различные возможные постановки задач поиска этой разметки.
1) Найти наиболее вероятное состояние всех скрытых параметров модели, а именно,
изображений x1T,x2T,...,xlT
и разметки kT, в соответствии с их апостериорным распределением
вероятностей  . То есть, требуется найти
. То есть, требуется найти
 .
.
После этого предъявить найденную разметку k*T в качестве результата распознавания.
В случае, когда порядок структуры поля зрения больше единицы, решение этой задачи неизвестно.
Однако решение этой задачи не имеет статистического смысла, так как для нахождения разметки используется наиболее вероятное состояние всех скрытых параметров системы [5]. Следующая постановка задачи является более разумной.
2) Найти наиболее вероятную разметку в соответствии с ее апостериорным распределением
вероятностей 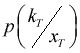 при условии заданного изображения xT. Это наиболее распространенная
формулировка задачи, называемая оценкой максимального правдоподобия.
при условии заданного изображения xT. Это наиболее распространенная
формулировка задачи, называемая оценкой максимального правдоподобия.

Эта задача еще сложнее предыдущей в том смысле, что невозможно даже сравнить апостериорные вероятности двух произвольных разметок.
3) С другой стороны, нахождение наиболее вероятной разметки - решение задачи 2) тоже не
является естественным. Это всего -навсего обозначает решение Байесовской задачи распознавания с
простейшей штрафной функцией 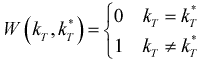 . Согласно этой штрафной функции
сегментация, отличающаяся от действительной в одном лишь пикселе считается столь же плохой, как и
сегментация, отличающаяся от действительной во всех пикселах. Разумнее было бы рассмотреть
Байесовскую задачу с аддитивной штрафной функцией
. Согласно этой штрафной функции
сегментация, отличающаяся от действительной в одном лишь пикселе считается столь же плохой, как и
сегментация, отличающаяся от действительной во всех пикселах. Разумнее было бы рассмотреть
Байесовскую задачу с аддитивной штрафной функцией  . Решение такой задачи
требует нахождения апостериорного распределения вероятностей разметки в каждом пикселе [5]:
. Решение такой задачи
требует нахождения апостериорного распределения вероятностей разметки в каждом пикселе [5]:
 .
.
Если 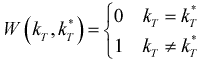 , то получим, что штраф пропорционален количеству неправильно
распознанных пикселей. Решение байесовской задачи будет следующим
, то получим, что штраф пропорционален количеству неправильно
распознанных пикселей. Решение байесовской задачи будет следующим
 .
.
Эта задача также вычислительно неразрешима.
6. Сведение вышеизложенных задач оптимизации к задачам генерирования
Заменим задачи 1), 2) и 3) на задачи 1*), 2*) и 3*) соответственно. Условие нахождения наиболее вероятного состояния заменим на умение генерировать состояние с заданной вероятностью.
Получим следующие три задачи:
1*) Построить конструктивный алгоритм генерирования изображений
x1T,x2T,...,xlT
и разметки kT в соответствии с их апостериорным распределением вероятностей
 .
.
2*) Построить конструктивный алгоритм генерирования разметки kT в соответствии с ее
апостериорным распределением вероятностей 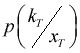 .
.
3*) Построить конструктивный алгоритм генерирования метки k в пикселе t в соответствии с ее апостериорным распределением вероятностей pt(k).
Знание ответа в любой из задач 1), 2) или 3) не позволяет решить остальные две задачи. В случае
же с задачами 1*), 2*) и 3*) все обстоит иначе. Умея генерировать изображения
x1T,x2T,...,xlT и разметку
kT согласно распределению  , то есть зная ответ к задаче 1*), легко построить также
решения задач 2*) и 3*). Для того чтобы сгенерировать разметку kT в соответствии с распределением
, то есть зная ответ к задаче 1*), легко построить также
решения задач 2*) и 3*). Для того чтобы сгенерировать разметку kT в соответствии с распределением
 , достаточно сгенерировать изображения
x1T,x2T,...,xlT
и разметку
kT согласно распределению
, достаточно сгенерировать изображения
x1T,x2T,...,xlT
и разметку
kT согласно распределению  и затем предъявить разметку
kT в качестве результата генерирования в задаче 2*). Далее, для того чтобы сгенерировать метку в пикселе
t в соответствии с распределением pt(k) можно прогенерировать разметку
kT в соответствии с распределением
и затем предъявить разметку
kT в качестве результата генерирования в задаче 2*). Далее, для того чтобы сгенерировать метку в пикселе
t в соответствии с распределением pt(k) можно прогенерировать разметку
kT в соответствии с распределением 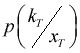 и затем предъявить метку kt в пикселе t в качестве результата
генерирования в задаче 3*).
и затем предъявить метку kt в пикселе t в качестве результата
генерирования в задаче 3*).
Заметим теперь, что прогенерировав несколько раз метку в пикселе t с распределением
pt(k) можно оценить это распределение вероятностей и использовать полученную оценку для решения
задачи 3). Таким образом, решение задачи 3*) позволяет решать задачу 3) с некоторой степенью
достоверности. Точно также, хотя и менее очевидно, решение задачи 2*) позволяет решить задачу 2), а
решение задачи 1*) позволяет решать задачу 1). Для решения задачи 2) необходимо генерировать много
раз разметку в соответствии с распределением вероятностей  и после этого в качестве решения
задачи 2) указать ту разметку, которая встретится большее количество раз. Аналогично, для решения
задачи 1) необходимо генерировать много раз изображения
x1T,x2T,...,xlT и разметку
kT в соответствии с распределением вероятностей
и после этого в качестве решения
задачи 2) указать ту разметку, которая встретится большее количество раз. Аналогично, для решения
задачи 1) необходимо генерировать много раз изображения
x1T,x2T,...,xlT и разметку
kT в соответствии с распределением вероятностей
 и после этого в качестве решения задачи 1) указать
такой комплект изображений x1T,x2T,...,xlT и
kT, который встретится большее количество раз. При этом
умение генерировать используется для оценки распределения вероятностей. Очевидно, что невозможно
решать задачу 1) и 2) при помощи алгоритма, описанного в последних трех предложениях, так как
объем требуемой выборки становится фантастически большим. Возможно, это происходит как раз из -за
того, что задачи 1) и 2) являются неразумно поставленными Байесовскими задачами распознавания.
и после этого в качестве решения задачи 1) указать
такой комплект изображений x1T,x2T,...,xlT и
kT, который встретится большее количество раз. При этом
умение генерировать используется для оценки распределения вероятностей. Очевидно, что невозможно
решать задачу 1) и 2) при помощи алгоритма, описанного в последних трех предложениях, так как
объем требуемой выборки становится фантастически большим. Возможно, это происходит как раз из -за
того, что задачи 1) и 2) являются неразумно поставленными Байесовскими задачами распознавания.
Далее мы будем решать только задачу 3), построив решение задачи 3*).
7. Описание метода генерирования и его усовершенствование
В данном разделе будет показано, что в построенной модели текстурного изображения
распределение вероятностей  задается марковским случайным полем. Поэтому, для
того, чтобы генерировать изображения x1T,x2T,...,xlT
и разметку kT согласно распределению
задается марковским случайным полем. Поэтому, для
того, чтобы генерировать изображения x1T,x2T,...,xlT
и разметку kT согласно распределению  можно воспользоваться стандартным алгоритмом генерирования марковских
случайных полей, описанным в третьем разделе. Дальше будет показано, что в этом случае скорость
генерирования метки в одном пикселе пропорциональна |X|l-1l. Это обозначает, что введение каждой
дополнительной текстуры замедляет алгоритм генерирования в |X| раз. Можно, однако, видоизменить
алгоритм генерирования таким образом, чтобы скорость генерирования метки в одном пикселе линейно
зависела от количества текстур, а именно, была пропорциональна |X| l. Алгоритм такого ускорения
также будет описан в данном разделе.
можно воспользоваться стандартным алгоритмом генерирования марковских
случайных полей, описанным в третьем разделе. Дальше будет показано, что в этом случае скорость
генерирования метки в одном пикселе пропорциональна |X|l-1l. Это обозначает, что введение каждой
дополнительной текстуры замедляет алгоритм генерирования в |X| раз. Можно, однако, видоизменить
алгоритм генерирования таким образом, чтобы скорость генерирования метки в одном пикселе линейно
зависела от количества текстур, а именно, была пропорциональна |X| l. Алгоритм такого ускорения
также будет описан в данном разделе.
Покажем вначале, что распределение вероятностей  является марковским на
поле зрения T.
В самом деле, апостериорная вероятность изображений
x1T,x2T,...,xlT
и разметки kT равна
является марковским на
поле зрения T.
В самом деле, апостериорная вероятность изображений
x1T,x2T,...,xlT
и разметки kT равна
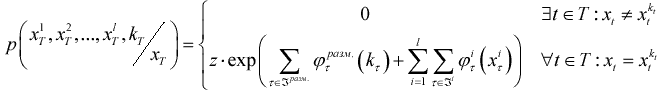 |
(5) |
z - нормирующий множитель.
Зададим теперь палитру в каждом пикселе таким образом, что в пикселе t 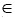 T
палитра состоит из таких наборов цветов
x1,x2,...,xl
и метки k, которые согласуются с меткой xt на наблюдаемом
изображении xT. Точнее, для пиксела t палитра равна
T
палитра состоит из таких наборов цветов
x1,x2,...,xl
и метки k, которые согласуются с меткой xt на наблюдаемом
изображении xT. Точнее, для пиксела t палитра равна  . Тогда
множество всех изображений в марковском поле совпадет с множеством тех изображений, для которых
выполняется условие
. Тогда
множество всех изображений в марковском поле совпадет с множеством тех изображений, для которых
выполняется условие
 |
(6) |
Формула (5) с учетом условия (6) перепишется в виде
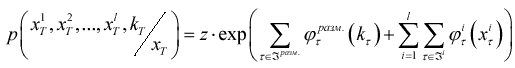 |
(7) |
что и говорит нам о том, что мы имеем дело с марковским случайным полем.
Из формулы (7) следует, что структура поля зрения равна
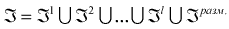 , а гиббсовские потенциалы определяются по формуле
, а гиббсовские потенциалы определяются по формуле
 . . |
Таким образом, распределение вероятностей  действительно является
марковским. Для генерирования поля, задаваемого этим распределением, требуется генерировать
вектор (x1t,x2t,...,
xlt,kt)
действительно является
марковским. Для генерирования поля, задаваемого этим распределением, требуется генерировать
вектор (x1t,x2t,...,
xlt,kt)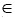 Xt
в пикселе t в соответствии с условным распределением вероятностей
Xt
в пикселе t в соответствии с условным распределением вероятностей
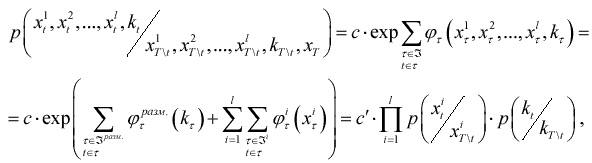 . . |
(8) |
где c и c' - нормирующие множители.
Непосредственное применение формулы (8) для генерирования метки в одном пикселе требует
|Xt| = |X| l-1 |K| = |X| l-1 l операций, так как для каждого вектора
(x1t,x2t,...,
xlt,kt)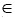 Xt необходимо
подсчитать вероятность
Xt необходимо
подсчитать вероятность  . Покажем теперь, что можно
генерировать сигнал в пикселе с распределением вероятностей (8) со скоростью, пропорциональной
|X| l .
. Покажем теперь, что можно
генерировать сигнал в пикселе с распределением вероятностей (8) со скоростью, пропорциональной
|X| l .
Улучшенное генерирование основывается на применении следующей простой формулы теории вероятностей: p(a,b) = p(a) p(b/a). Исходя из этой формулы можно генерирование случайной пары (a,b) в соответствии с распределением вероятностей p(a,b) производить таким образом: сначала прогенерируем значение a в соответствии с распределением p(a) , а затем прогенерируем b в соответствии с вероятностью p(b/a) для сгенерированного a.
Применение этой процедуры приводит к следующему алгоритму генерирования. Сначала
прогенерируем метку kt в соответствии с распределением  , затем цвета
(x1t,x2t,...,xlt,kt)
в соответствии с распределением
, затем цвета
(x1t,x2t,...,xlt,kt)
в соответствии с распределением  .
.
Подсчитаем вероятность метки в данном пикселе
 . . |
(9) |
Скорость алгоритма генерирования метки в данном пикселе в соответствии с формулой (9)
пропорциональна |X| l , так как для подсчета каждой из вероятностей 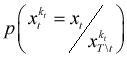 требуется |X|
операций.
требуется |X|
операций.
Распределение вероятностей цветов x1t,x2t,..., xlt при фиксированной метке kt равно
 . . |
(10) |
Формула (10) показывает, что при фиксированной метке kt цвета
независимы. Цвет каждой компоненты вектора
(x1t,x2t,...,xlt) -
xit, i<>kt генерируется в соответствии с распределением
вероятностей . Цвет
xktt при этом принимает значение xt.
Такой алгоритм генерирования цветов x1t,x2t,...,xlt
также требует |X| l операций. Описание усовершенствованного алгоритма
генерирования завершено.
. Цвет
xktt при этом принимает значение xt.
Такой алгоритм генерирования цветов x1t,x2t,...,xlt
также требует |X| l операций. Описание усовершенствованного алгоритма
генерирования завершено.
8. Экспериментальная проверка алгоритма текстурной сегментации
Как уже говорилось в разделе 7, мы решаем задачу 3), используя алгоритм генерирования - решение задачи 3*). Экспериментальная проверка алгоритма сегментации в первую очередь проводилась на искусственных примерах, так как для изображений реального мира спорным является вопрос настоящей разметки изображения.
1) В первом эксперименте вручную были заданы параметры двух марковских полей, отвечающих за два типа текстур и параметры одного марковского поля, отвечающего за сегментацию. После этого в 10 соответствии с выбранными параметрами марковского случайного поля были сгенерированы два изображения (рис.2 (a), (b)) и сегментация (рис.2 (c)). Из этих изображений согласно формуле (3) было построено изображение xT, по которому следует восстановить разметку. После этого методом генерирования были оценены апостериорные вероятности метки в каждом пикселе pt(k). На рисунке 2(е) показана восстановленная сегментация. При этом те пикселы, в которых апостериорная вероятность каждой метки меньше 0.95, обозначены черным цветом.
 |
 |
||
| (a) | (b) |
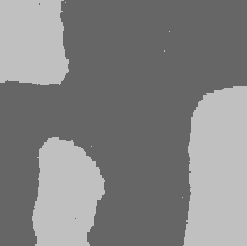 |
 |
 |
||
| (c) | (d) | (e) |
Рис. 2. Искусственный эксперимент с искусственными текстурами.
(a) и (b) Сгенерированные примеры текстур x1T
и x2T соответственно.
(c) Сгенерированный пример разметки kT.
(d) Искусственное изображение xT, полученное из изображений (a), (b) и (c) согласно
формуле (3).
(e) Восстановленная сегментация, черным цветом обозначены те пикселы, в которых
апостериорная вероятность каждой метки меньше 0.95.
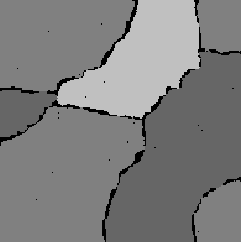
2) Во втором эксперименте параметры марковских полей были получены по примерам реальных текстур при помощи методов, описанных в работах [8,9,10,11]. Так же, как и в предыдущем примере были сгенерированы примеры текстур (рис. 3 (a), (b), (c)) и сегментации (рис. 3 (d)). Из этих изображений согласно формуле (3) было построено изображение T x, по которому следует восстановить разметку. После этого методом генерирования были оценены апостериорные вероятности метки в каждом пикселе. На рисунке 3 (f) показана восстановленная сегментация. При этом те пикселы, в которых апостериорная вероятность каждой метки меньше 0.95, обозначены черным цветом.
 |
 |
 |
||
| (a) | (b) | (c) |
 |
 |
 |
||
| (d) | (e) | (f) |
Рис. 3. Искусственный эксперимент с реальными текстурами.
(a), (b) и (c) Сгенерированные примеры трех текстур x1T,x2T
и x3T соответственно.
(d) Сгенерированный пример разметки kT.
(e) Искусственное изображение xT, полученное из изображений (a), (b), (c) и (d) согласно
формуле (3).
(f) Восстановленная сегментация, черным цветом обозначены те пикселы, в которых
апостериорная вероятность каждой метки меньше 0.95.
3) В следующем эксперименте для распознавания был выбран аэрофотоснимок. Параметры марковских полей были получены по примерам, взятым из изображения на рис. 4 (a) при помощи методов, описанных в работах [8,9,10,11]. Методом генерирования были оценены апостериорные вероятности метки в каждом пикселе. На рисунке 4 (b) показана восстановленная сегментация. При этом те пикселы, в которых апостериорная вероятность каждой метки меньше 0.95 обозначены черным цветом.
9. Заключение
До сих пор задача сегментации в основном рассматривалась, как задача нахождения наиболее вероятной разметки (maximum a posteriori probability estimation). Такая постановка задачи неадекватно отражает статистический смысл задачи восстановления разметки, так как является байесовской задачей с простейшей штрафной функцией, предполагающей, что разметка, отличающаяся от оптимальной лишь в одном пикселе столь же плоха, как и разметка, отличающаяся от оптимальной во всех пикселах. Более естественной штрафной функций является аддитивная штрафная функция, выражающая естественное представление о качестве восстановленной разметки, как о количестве правильно распознанных пикселей. Результатом данной работы является метод решения байесовской задачи восстановления разметки с аддитивной функцией штрафа. Решение этой задачи сводится к вычислению апостериорного распределения вероятности метки в каждом пикселе. Оценка этого апостериорного распределения вероятностей производится при помощи генерирования.
 |
 |
||
| (a) | (b) |
Рис. 4. Реальный пример с реальными текстурами.
(a) Исходное изображение.
(b) Восстановленная сегментация, черным цветом обозначены те пикселы, в которых
апостериорная вероятность каждой метки меньше 0.95.
10. Список литературы
1. Stan Z. Li, "Markov Random Field Modeling in Image Analysis", Computer Science Workbench,
Springer, 2001. 323 p.
2. Geman S., Geman D., "Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of
Images", IEEE Trans. on PAMI, 1984, vol. 6, no. 6, pp. 721-741.
3. Cerny V., "A thermodynamical approach to the traveling salesman problem: An efficient simulation
algorithm", Journal of Optimization Theory and Applications, 1985, vol.45, pp. 41-51.
4. Kirkpatrick S., Gellatt C.D., Vecch Jr., and M.P., "Optimization by simulated annealing", Science,
1983, vol. 220, no. 4598, pp. 671-680.
5. Schlesinger M.I., Hlavac V., "Deset prednasek z teorie statistickeho a strukturniho rozpoznavani",
Vydavatelstvi CVUT, Praha, 1999, 537 p.
6. ШлезингерМ.И., "Математические средства обработки изображений ", Киев, Наукова думка,
1989, 198 стр.
7. Bezag J., "On the statistical analysis of dirty pictures", Journal of the Royal Statistical Society, Series
B 48, pp. 259-302, 1986.
8. Gimel'farb G.L., "Texture Modelling by Multiple Pairwise Pixel Interactions", IEEE Trans.on Pattern
Anal. Machine Intell., 1996, 18:11, pp.1110-1114
9. Gimel'farb G.L., "Modeling image textures with Gibbs random fields", Pattern Recognition Letters,
1999, 20:12, pp.1123 - 1132.
10. Gimel'farb G.L., "Image Textures and Gibbs Random Fields", Kluwer Academic Publishers:
Dordrecht, 1999. 250 p.
11. Zalesny A., "Analysis and Synthesys of Textures With Pairwise Signal Interactions", Technical
report: Project 50542(EC ACTS 0740-«Vanguard», 1.3.1998-1.3.1999)
12. Zalesny A., Luc Van Gool, "A Compact Model for Viewpoint Dependent Texture Synthesis",
SMILE 2000 Workshop, Lecture notes in computer science, Vol. 2018, pp. 124-143, 2001.
| Библиотека | Реферат | Ссылки | Отчет о поиске | Индивидуальное задание |