МЕТОДЫ АНАЛИЗА И СИНТЕЗА ТЕКСТУР

А.В. Яковлев

Первоисточник: http://jakovlev.boom.ru/science/paper/paper1.pdf

2 При анализе изображений важной их характеристикой служит текстура, которая присутствует во всех изображениях, начиная с изображений, получаемых с помощью самолетных и спутниковых устройств и кончая микроскопическими изображениями в биомедицинских исследованиях. Однако, несмотря на это, концепция текстуры не очень хорошо определена и понимается даже сегодня. Харалик писал в [1]: «несмотря на повсеместное присутствие в изображениях и важность текстуры, формального подхода к описанию текстуры и строгого ее определения пока не существует, и методы различения текстур, как правило, разрабатываются отдельно для каждого конкретного случая...». Это, в большей мере, является следствием факта, что неизвестна природа информации воспринимаемой человеческой визуальной системой, когда мы рассматриваем зону изображения.

Из литературы можно выделить два типа определений текстуры:

- Во-первых, это интерпретация текстуры как повторения базовых примитивов, имеющих различную ориентацию в пространстве. То есть это определение настаивает на структурированной природе текстуры. Примерами в этом случае могут служить текстуры ткани, кирпичной стены и т.д. Сторонники такого определения ориентировали себя на спектральный анализ и представление текстуры [2].

- Во-вторых, текстура рассматривается как некий анархичный и однородный аспект, не обладающий ярко выраженными краями. Для сторонников этого метода, не существует заметных образцов или доминирующей частоты в текстуре (например дерн, кора, земля и так далее, рассматриваемые с большого расстояния), т.е. они ориентировали себя на вероятностный метод решения проблемы текстуры [3].

Фактически, лучшее определение термина «текстура» достигается синтезом обоих описанных выше методов. Текстура должна считаться двухуровневой структурой. То есть она представляет собой пространственную организацию (высший уровень) базовых примитивов (или непроизводных элементов как их называет Харалик [1]), которые сами имеют случайный аспект (низший уровень) [4].

На качественном уровне текстуры можно разделить на мелкозернистые, крупнозернистые, гладкие, гранулированные, холмистые. Такое разделение базируется на признаках базовых примитивов или пространственном взаимодействии между ними. Например, при увеличении числа различимых непроизводных элементов в пределах небольшого участка изображения и при их беспорядочной структуре получается мелкозернистая текстура. По мере того как пространственная структура становится все более определенной, а базовые элементы охватывают все большее число элементов растра, зернистость текстуры возрастает.

По степени взаимодействия базовых элементов различают слабые и сильные текстуры. В слабых текстурах пространственное взаимодействие непроизводных элементов мало. Чтобы различать такие текстуры, достаточно определить частоту повторения того или иного непроизводного элемента на некотором локальном участке изображения. Сильными называются такие текстуры, в которых пространственные взаимодействия не случайны. Для различения таких текстур достаточно вычислить частоту повторения каждой пары непроизводных элементов, связанных определенным пространственным отношением.

Текстурные математические модели обычно применяется для воспроизводства внешнего вида текстуры. Натуральные текстуры проявляют локальные свойства, которые можно обычно моделировать случайными процессами, хотя с других точек зрения эти характеристики далеко не случайны. Ниже приведено краткое описание наиболее часто встречаемых в литературе текстурных моделей [5].Текстурные математические модели обычно применяется для воспроизводства внешнего вида текстуры. Натуральные текстуры проявляют свойства, которые процессами, хотя с других точек зрения эти характеристики далеко не случайны. Ниже приведено краткое описание наиболее часто встречаемых в литературе текстурных моделей [5].

Time-series модель рассматривает периодичность в пространственном сканировании изображения. В процессе сканирования, каждый последующий пиксель V_N+1 определяется на основе предшествующих - V₁…V_N. Текстурное поле моделируется построчно, пиксель за пикселем, пока все строки не будут заполнены. Недостатком такой модели является то, что она плохо описывает структуру текстуры в направлении (направлениях) перпендикулярных сканированию.

Для моделирования натуральных ячеистых текстур используется ячеистая модель. Моделирование происходит в два этапа. На первом текстурное поле разделяется на некоторое количество ячеек и для каждой из них вычисляется центр инерции (ядро). На втором этапе происходит последовательное сканирование изображения и сравнения расстояния от точки до всех центров инерции. В результате пиксель назначается в группу, соответствующую ближайшему ядру. Проведенные эксперименты показали хорошее визуальное сходство смоделированной текстуры с натуральной ячеистой текстурой [5].

Синтаксические текстурные модели сравнивают символы формальной грамматики со структурными примитивами текстуры. Для моделирования текстур были расширены и переработаны ряд правил грамматики применительно к теории вероятности. Синтаксические модели применяются для описания сильно структурированных текстур.

Двумерная модель случайного марковского поля рассматривает условные вероятности яркостей на элементарном текстурном образце. Марковские свойства модифицируются определением переходной вероятности на окрестности смежных или несмежных точек. Этот метод достиг хороших результатов в моделировании прототипов текстур. Однако он практически не применяется на практике в связи с большим размером модели (количе ст во условных вероятностей равно G^S, если G – количе ст во уровней яркости, а S – количе ст во рассматриваемых (связанных) точек.

Для измерения и описания текстур изображения применяются ряд методов. Среди них можно выделить следующие группы:

- методы, основанные на измерении пространственной частоты (в мелкозернистых текстурах преобладают высокие, а в крупнозернистых текстурах - низкие пространственные частоты);

- методы, основанные на вычислении количе ст ва перепадов на единицу площади изображения (на крупнозернистых текстурах эта величина мала, с уменьшением зернистости текстуры она возрастает;

- методы, использующие матрицу смежности значений яркости (с ростом расстояния между оцениваемыми точками, в крупнозернистых текстурах изменение распределения яркости происходит значительно медленнее чем в мелкозернистых);

- методы, описывающие текстуры длинами серий (строки с постоянной яркостью точек, на крупнозернистых текстурах эти серии длиннее чем на мелкозернистых);

- авторегрессионые методы для описания текстуры используют коэффициенты линейных оценок яркости точечного элемента изображения по заданным значениям элементов некоторой его окрестности (эти коэффициенты почти одинаковы для крупнозернистых и существенно различны для мелкозернистых текстур);

- методы, основанные на гистограмме пространственной разности яркостей;

- методы, отыскивающие регулярность в форме структурных элементов;

- методы, основанные на анализе микроструктуры текстурного поля.

Достоинство пространственной частоты как средства описания текстуры состоит в привычности этого понятия. Однако при этом возникает существенная трудность, связанная с квантованием яркости изображения. Процедуры квантования не инвариантны даже по отношению к монотонным преобразованиям яркости.

Одним из таких методов является метод описание текстуры с помощью автокорреляционной функции. Значение автокорреляционной функции характеризует размер базовых примитивов, который, в свою очередь, определяет зернистость текстуры, т.е. крупнозернистые текстуры содержат более крупные базовые элементы, а мелкозернистые – более мелкие. Если непроизводные элементы изображения относительно велики, значение автокорреляционной функции с увеличением сдвига уменьшается достаточно медленно. Если же тоновые непроизводные элементы малы, то функция уменьшается быстрее.

Автокорреляционная функция определяется следующим выражением:

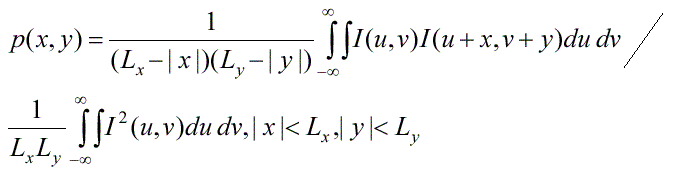
где I (u, v) - прозрачность диапозитива в точке с координатами (u, v), (вне прямоугольной площади диапозитива
0 <=u <=L и 0 <=v<=L прозрачность равна нулю)

(х, у) - величина сдвига в направлении и в направлении у.

Еще одним методом, основанным на измерении пространственной частоты, является оптический метод анализа текстуры. Этот метод основан на том, что при освещении фрагмента изображения, мы получаем создаваемое линзой распределение света, которое известно под названием «дифракционная картина Фраунгофера». Из дифракционной картины можно выделить вектор признаков, который может использоваться для распознавания фрагментов.

К этой группе методов можно также отнести метод цифровых преобразований. При анализе текстуры этим методом изображение разбивают на небольшие непересекающиеся квадратные фрагменты размера n*n пикселей. Полученные таким образом n² -мерные вектора при преобразовании выражают В некоторой новой системе координат. В преобразовании Фурье используется базис из тригонометрических функций синус и косинус, в преобразовании Адамара - базис из функций Уолша и т. д. Суть преобразований в том, что базисные векторы новой координатной системы хорошо интерпретируются в терминах пространственной частоты или порядка следования.

В качестве характеристики текстуры может использоваться количество перепадов яркости на единицу площади изображения. Приходящийся на пиксель изображения перепад можно обнаружить, сравнивая значения локальных признаков двух непересекающихся фрагментов изображения, соседствующих с этой клеткой.

В качестве локального признака может использоваться, например, градиент Робертса (сумму абсолютных значений разностей между уровнями яркости пар соседних клеток, расположенных по обе стороны от каждой диагонали) или следующие, схожие с градиентом характеристики яркости в некоторой окрестности элемента изображения:

где g_c - яркость некоторого элемента изображения, N - число элементов изображения в его окрестности, - средняя яркость этих элементов, а - некоторая метрика.

Один из аспектов текстуры связан с пространственным распределением и пространственной взаимозависимостью значений яркости локальной области изображения. Статистики пространственной взаимозависимости значений яркости вычисляются по матрицам переходов значений яркости между ближайшими соседними точками. Матрица смежности (или матрица совместной встречаемости) уровней яркости представляет собой оценку плотности распределения вероятностей второго порядка, полученную по изображению в предположений, что плотность вероятности зависит лишь от расположения двух пикселей. Обозначим эту матрицу 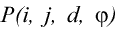, где i и j – яркости соседних точек на изображении, расположенных на расстоянии d друг от друга, при угловом направлении . Поскольку число таких матриц может быть очень большим, то обычно ограничиваются лишь рассмотрением пикселей, находящиеся в непосредственной близости либо усредняют матрицы, составленные для различных ориентаций [6]. Совершенно очевидно, что такие матрицы содержат информацию характеризующую текстуру. По матрице совместной встречаемости вычисляется около двадцати признаков, ниже приведены наиболее употребимые из них:

- степень однородности или энергия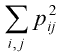

- энтропия

- максимальная вероятность max P_ij

- обратный момент разности

- коэффициент корреляции

- вероятность серии длинны n с яркостью i (изображение марковско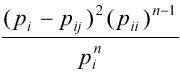е) где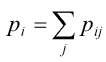

Серия - это максимальная связанная совокупность вытянутых в прямую линию пикселей одинаковой яркости. Серия характеризуется яркостью, длинной и направлением. Обозначим N_g – число возможных значений яркости, N_r – число возможных длин серий, а p(i, j) – число серий длинны j с яркостью i. Харалик [1] предложил следующие статистики величины p(i, j) для анализа текстур:

(обратные моменты увеличены при коротких сериях),

(моменты увеличены при длинных сериях),

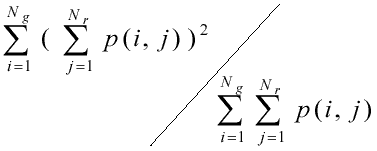
(неоднородность яркости),

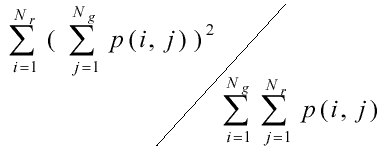
(неоднородность длинны серий).

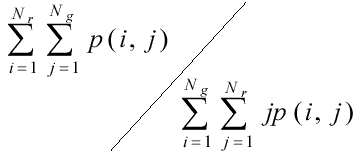
(доля изображения в сериях).

В рамках линейной авторегрессионной модели по любой заданной линейной оценке легко синтезировать текстуру. В этом смысле авторегрессионный подход позволяет получить всю информацию о текстуре. Используется одномерная и двумерная авторегрессионные модели. При использовании одномерной модели яркость следующего пикселя определяется как сумма линейной комбинации значений яркости предыдущих пикселей изображения. При использовании двумерной модели яркость пикселя определяется не просто предыдущим участком сканирования, а зависит от яркости его двумерной окрестности, состоящей из пикселей сверху и слева от рассматриваемого. Как показали исследования, двумерная авторегрессионная модель дает лучшие результаты по сравнению с одномерной.

Для анализа текстур гистограмма рассматривается не как плотность вероятности уровней яркости, измеренных в каждом элементе рассматриваемого фрагмента, а как плотность вероятности разности уровней яркости между точками каждой пары элементов, разделенных заданным расстоянием 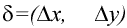, то есть строится 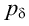, где (x, y– координаты элемента изображения). Поведение 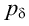гораздо ярче характеризует текстуру, чем обычная гистограмма. Для крупнозернистой текстуры (если 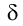много меньше размеров текстуры) большинство разностей малы, а для мелкозернистой текстуры (когда 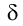сравнима с размерами элемента) – велики. Для оценки поведения текстуры могут использоваться следующие величины, вычисляемые на основе построенной гистограммы:

- контраст

- второй угловой момент

- среднее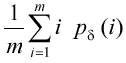

Таким образом можно акцентировать различные свойства текстуры и использовать их в качестве признаков текстуры. Например, если текстура направленная, степень разброса значений 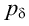изменяется с направлением 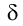, так как направленность текстуры означает разную степень грубости в различных направлениях.

Вычисляя признаки для различных расстояний и углов, можно получить многомерный вектор признаков текстур. Проведенные эксперименты [7] показывают четкую связь между числовыми значениями этих признаков и визуальными особенностями текстуры. Основная идея этого подхода состоит в следующем. Определенной формы совокупность элементов изображения (например, образующая линию или квадрат) называется структурным элементом. Путем переноса структурного элемента по изображению и стирания этим элементом фигур, образованных прилегающими друг к другу элементами растра со значением 1, получают новое бинарное изображение. Соответствующим образом параметризируя структурный элемент и определяя зависимость числа элементов в стертом изображении от введенного параметра, можно вычислить текстурные признаки. Используя более сложные структурные элементы, можно получить обобщенную ковариационную функцию, которая содержит суммарную информацию о текстуре изображения.

Эти методы метод просты в вычислительном отношении и достаточно точены. В экспериментах по классификации восьми естественных текстур получена точность классификации, превышающая 95% [8].

Один из вариантов этих методов предполагает параллельную свертку поля текстуры с девятью масками 3*3. Две маски выделяют горизон - тальные и вертикальные краевые градиенты Собела, третья выступает в роли оператора Лапласа и еще одна служит оператором взвешенного пространственного усреднения. Затем в пределах окна, обычно 17*17, вычисляют стандартное отклонение для каждой свертки поля, в результате чего образуется девятимерный вектор признаков анализируемого образца текстуры.

Текстурный синтез очень важен в обработке изображения, он может применяться, например, для восстановления изображений по характеристикам их текстур, или для генерации искусственных изображений используемых в компьют ерных симуляторах и компьют ерном видео.

Для синтеза нам необходимо знать набор характеристик текстуры, используемых как входные параметры для процедур генерации искусственных текстур. Этот набор статистик, снимаемых с натурального текстурного поля, должен правильно моделировать текстуру в соответствии с нашей визуальной системой. Проведенные эксперименты [4] по распознаванию текстур показали, что человеческая визуальная система чувствительна лишь к статистикам второго порядка, то есть на практике, визуально практически не возможно различить две текстуры имеющие различные статистики более высоких порядков и одинаковые моменты второго порядка. Таким образом, можно заключить следующее: существует минимальный набор параметров, такой что, если для двух текстур, этот набор является одинаковым, то они воспринимаются как идентичные, но если по крайней мере одни из этих параметров различны, то две текстуры будут восприниматься как различные.

Этот метод предложен Андре Гогаловичем и Сонг де Ма [4] и применяется для генерации искусственных текстур, используя априорно заданные статистики второго порядка (средние или автокорреляционные параметры второго порядка) натурального текстурного поля в качестве входных данных.

Разработанная процедура генерации позволяет синтезировать текстурное поле Tx такое, что его характеристический вектор B^Tx соответствует априорно заданному вектору B. Синтез осуществляется в два этапа. Во -первых, создается текстурное поле, которое является реализацией однородного белого шума, где только гистограмма (пространственные средние первого порядка) равны заданным. Гистограмма может быть вычислена из матрицы смежности, которая извлекается из заданного вектора B используя (4.1).

(4.1)

Затем, на втором шаге, текстура последовательно модифицируется пиксель за пикселем, пока минимизируется средняя квадратичная ошибка между векторами B и B^Tx. Проблема синтеза считается решенной, если ошибка сходится к нулю.

Ниже предложенная процедура синтеза рассматривается более подробно.

Первый этап. Для стохастического процесса распределение вероятности первого порядка p^Tx(x_i=L₁) и распределение вероятности второго порядка 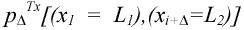не зависит от расположения i. Обозначив их соответственно p^Tx(L₁) и p^Tx(L₁,L₂) имеем:

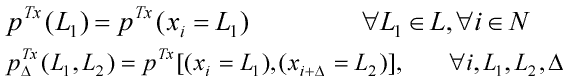		(4.2)
		(4.3)

Из заданного характеристического вектора B можно вычислить значение) 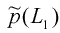гистограммы натуральной текстуры, используя (4.1). После этого, используя стохастический процесс первого порядка, генерируется поле случайного белого шума, чье распределение вероятности первого порядка равно 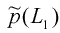(используется в качестве входных данных в процедуре синтеза). Таким образом после первого этапа синтеза имеем:

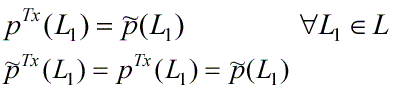(4.4)

Синтезируемая текстура Tx является такой, что ее гистограмма равна заданной гистограмме 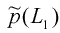. Так как она является набором взаимно-независимых случайных переменных имеющих тот же закон распределения, то равносильно следующее соотношение:

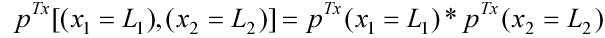(4.5)

Из свойства эргодичности Tx имеем:

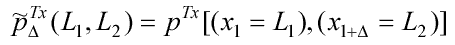(4.6)

Таким образом можно вычислить значение параметров характеристического вектора B^Tx синтезируемого текстурного поля Tx используя:

(4.7)

Если заданный характеристический вектор B оказался равным B^Tx, то процедура синтеза останавливается после первого шага. Иначе осуществляется переход ко второму этапу.

Второй этап . В общем случае B<>B^Tx после первого этапа, то есть .

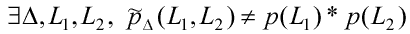На втором шаге происходит последовательная, пиксель за пикселем, модификация текстурного поля, минимизируя среднюю квадратичную ошибку . Значение В обновляется каждый раз, когда модифицируется значение яркости, в соответствии с (4.7).

Допустим на текстурном поле точка x_i имеет яркость L₁, и необходимо найти новое значение яркости L*₁ для этой точки в процессе минимизации . Так как пространственные средние второго порядка для B и B^Tx связаны с определенной окрестностью, то необходимо рассматривать все точки окрестности, в соответствии с принятыми направлениями.

Обозначим B^Tx(L₁) значение характеристического вектора, когда яркость точки x_i равна L₁. Предположим, что мы заменили L₁ на L'₁. Теперь необходимо определить порядок выбора оптимальной яркости L*₁ для точки x_i.

Каждое направление, определенное в заданной окрестности, соответствует только двум точкам текстурного поля связанным с x_i то есть и .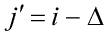

Предположим, что x_j =L₂ и x_j' =L₃. Если заменить L₁ на L^'₁, встречаемость в матрице смежности 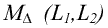измениться на (L^'₁,L₂) и соответственно (L₁,L₃) на (L^'₁,L₃). Таким образом, матрица смежности обновиться в соответствии с (4.8)

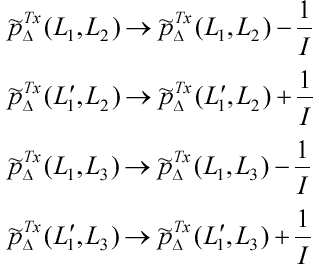(4.8)

где I – количество направлений , рассматриваемых на текстурном поле (если =(n,m) и если текстурное поле Tx имеет размер N*M, то I=(N-||n||)*M-||m||).

Для получения желаемого значения L^*₁ необходимо вычислить B^Tx(L₁) для L^'₁=0,1…L-1 (L^'₁<>L₁) и затем

В результате яркость L₁ заменяется на L^*₁, такую что

Если Err (L₁) имеет минимальное значение, то яркость в x_iне модифицируется.

Далее осуществляется переход в новую точку текстуры, то есть происходит сканирование всего изображения.

На практике не приходится вычислять значение ошибки в каждой точке изображения (что значительно замедляет обработку), а необходимо лишь обновлять ее в соответствии с (4.9).

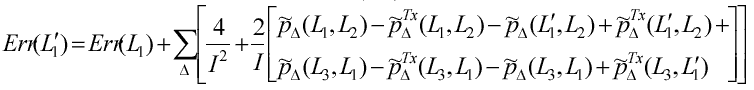(4.9)

Приведенный выше метод синтеза полутоновых текстур может быть с некоторыми дополнениями применен для синтеза цветных текстур. При синтезе цветных текстур R-G-B компоненты каждого пикселя кодируются в соответствии с некоторым алгоритмом, что позволяет заменить три (N*M) массива цветной текстуры (где N,M – размеры текстурного поля) на один (N*M) - массив кодов. Таким образом получается модель цветной текстуры, которая имеет такой же размер как и полутоновая текстура. Далее для этой модели может быть вычислен характеристический вектор B и применена приведенная выше процедура синтеза текстурного поля, где вместо значений яркости пикселей будут использоваться соответственно значения кодов пикселей.

Для кодирования цветной текстуры может быть применен динамический группирующий алгоритм рассмотренный в [9].

Предположим, что мы имеем L кодов. То гд а для инициализации группирующего алгоритма каждое значение пикселя X_i кодируется величиной Y_i = R + 256G + 2¹⁶B. Затем все значения Y_i ранжируются по возрастанию значений [Y_min,Y_max], и подразделяются на L равных сегментов. Далее каждый пиксель, лежащий в l-ом интервале назначается в группу Z_l.

Динамический группирующий алгоритм представляет собой итеративную процедуру, которая однозначно сходится после 5-8 итераций.

Ниже приведена последовательность шагов алгоритма:

1. Для каждой группы Z_l вычисляется ее центр инерции I_l.
2. Для каждой точки X_i сравнивается расстояние до всех центров инерции I_l.
3. Точ к а X_i назначается в группу, содержащую ближайший центр инерции.
4. Далее 1.

На выходе процедуры мы получаем желаемый результат. Каждый пиксель X_i кодируется одним из L возможных кодов (создается NT*MT массив кодов) и для каждого кода l сохраняются (R_l, G_l, B_l) значения финального центра инерции I_l. Таким образом получаются таблицы, которые позволят на этапе декодирования визуализировать цветную текстуру.

В настоящее время текстурная информация широко применятся в алгоритмах обработки изображения и машинной графики. Класс задач, решаемых при помощи текстуры достаточно велик. Наиболее часто применение текстуры можно встретить в задачах сегментации и моделирования трехмерных изображений (термин «трехмерные изображения» обозначает не собственно трехмерные изображения, а их двухмерные проекции).

Сегментация позволяет выделить участки изображения, кажущиеся наблюдателю одинаковыми; эта операция обеспечивает разбиение изображения на однородные области. Однородность области можно определить в категориях уровней яркости, а можно на основе текстурной информации рассматриваемой области. То есть можно сказать, что области воспринимаются наблюдателем как однородные если они обладают схожей текстурой.

Например, при использовании матрицы совместной встречаемости уровней яркости для определения характеристик текстуры, можно сформировать их для каждой группы областей отдельно, после чего сравнить построенные матрицы или вычисленные на их основе характеристики между собой. Если сравнение дало положительный результат, то объединение соответствующих областей представляет собой однородную область.

В общем случае, пусть F(R) – признак, оцениваемый на области R (в приведенном выше примере таким признаком является матрица совместной встречаемости). Если R₁₂ является объединением двух смежных, но непересекающихся областей R₁ и R₂, то критерий однородности можно задать, потребовав, чтобы оценка значения признака F(R₁₂) была близка оценкам значений признаков F(R₁) и F(R₂). Пусть R₁ – уже выделенная область, а R₂ – небольшая область, для которой проверяется возможность присоединения к R₁. Необходимо выбрать значение порога T таким образом, чтобы при абсолютном значении разности F(R₁) и F(R₂), меньше T, принималось решение об однородности области. Пороговое значение T должно быть больше дисперсии значений признака F(R), определяемой шумом.

Проблеме использования текстуры в алгоритмах сегментации посвящен ряд работ [4, 11, 12].

В [12] рассматривается применение двумерной линейной модели предсказания в сегментации текстурных изображений. Процесс сегментации осуществляется в два этапа. На первом шаге осуществляется деление исходного изображения на элементарные прямоугольные области достаточно малого размера. Предполагая, что каждая такая область однородна, оцениваются ее текстурные характеристики. Далее происходит слияние анализируемых областей, если их текстуры (или что то же самое – текстурные свойства) схожи. Таким образом, на первом этапе происходит «грубая» сегментация. На втором шаге сегментированное изображение корректируется пиксель за пикселем, с целью отыскания более лучших границ областей.

В качестве меры подобия двух смежных областей A и B в данной работе используется величина (область C является объединением областей A и B):

где 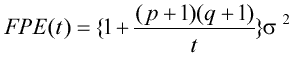ошибка предсказания;

- дисперсия входного сигнала;
t - количество пикселей в области;
p, q - размеры области.

Работа [11] посвящена исследованию применимости цветового свойства текстуры для сегментации биомедицинских изображений. Предлагаемая процедура сегментации состоит из следующих шагов: преобразование цветов (кодирование R-G-B составляющих исходного изображения), сегментация по яркости, сегментация цветной текстурой (выбирается текстурный образец, кодируются его R-G-B составляющие, осуществляется сегментация), маскирование (исключается шум – области имеющие малый размер), восстановление (восстановление изображения на основе изображения, полученного на втором этапе) и окраска (декодирование изображения).

Текстура может применяться для придания воспроизводимым трехмерным изображениям вида естественных сцен, что позволяет создать впечатление подлинной глубины.

Как отмечалось выше, текстура соответствует статистикам второго порядка, характеризующим распределение яркости на изображении. Чтобы некоторое синтезированное изображение давало зрительное впечатление текстуры, необходимо присваивать пикселю значение цвета или уровня яркости, исходя из цвета и яркости соседних с ним пикселей. Один из способов предусматривает фиксацию геометрии, определяемой S(u, v), и изменение цвета в соответствии со значениями функции C(u, v). Значения функции C(u, v) могут быть табулированы или порождаться с помощью некоторого случайного процесса. Более реалистичный подход предусматривает изменение формы поверхности, например, введением выпуклостей и складок, и создание текстурного эффекта за счет вариаций отраженного света. Один из способов моделирования такой грубой поверхности заключается в возмущении поверхности по направлению ее нормали при помощи заданной функции P(u, v). Для определения кажущейся яркости следует найти значения нормали к поверхности, подвергаемой возмущению. Уравнение одной из компонент нормали возмущенной поверхности можно записать в следующем виде:

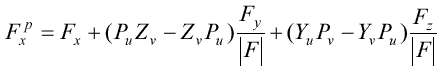где F_x, F_y, F_z,|F| - компоненты нормали к поверхности и ее норма;
P_u, P_v - частные производные P(u, v) по u и v соответственно.

Подобные уравнения можно записать и для других компонент нормали. Это означает, что нормаль к возмущенной поверхности можно определить по нормали к невозмущенной поверхности при помощи умножения последней на симметричную матрицу 3*3. Главная диагональ матрицы состоит из единиц, а выражения для всех остальных ее элементов можно получить из приведенного выше уравнения и аналогичных для компонент F^p_y и F^p_z.

В работе дан обзор наиболее часто используемых методов, применяемых для анализа и моделирования текстур. Проведенные исследования позволяют сделать следующие выводы:

- Достоинство пространственной частоты как средства описания текстуры состоит в привычности этого понятия. Однако при этом возникает существенная трудность, связанная с квантованием яркости изображения. Процедуры квантования не инвариантны даже по отношению к монотонным преобразованиям яркости. С целью компенсации возникающих эффектов можно применить вероятностное квантование, однако инвариантность квантованного изображения по отношению к монотонным преобразованиям достигается при этом ценой потери точности в передаче градаций яркости.

- Достоинство подхода к описанию текстуры с помощью структурных элементов состоит в том, что особое значение придается форме непроизводных элементов. Однако его слабость в том, что он применим только к двух градационным изображениям.

- Вычисление матрицы смежности позволяет охарактеризовать пространственные зависимости внутри совокупности значений яркости текстурного изображения, причем сделать это можно инвариантно к монотонным преобразованиям яркости. Недостаток такого подхода в том, что теряется информация о форме тоновых непроизводных элементов, что, по -видимому, должно приводить к существенному ухудшению результатов анализа текстур с непроизводными элементами большого размера.

- В рамках линейной авторегрессионной модели по любой заданной линейной оценке легко синтезировать текстуру. В этом смысле авторегрессионный подход позволяет получить всю информацию о текстуре. Однако описанию поддаются, как правило, лишь микроскопические текстуры.

- Достоинством подхода, основанного на гистограмме пространственной разности, является его простота и не трудоемкость. Кроме того была выявлена четкая связь между числовыми значениями вычисленных признаков и визуальными особенностями текстуры.

Литература

1. Харалик Р. М. Статистический и структурный подходы к описанию текстур ТИИРЭ 5, 1979, 98-118.
2. F. D’Astous and M.E. Jernigan Texture Discrimination Based on Detailed Measures of the Power Spectrum 83-86.
3. Patric C. Chen and T. Pavlidis. Segmentation by Texture Using Correlation. 551-553.
4. Andre Gagalowicz and Song De Ma. Sequential Synthesis of Natural Textures Computer Vision, Graphics and Image Processing 30, 1985, 289-315.
5. John-Peter Lewis Texture Synthesis for Digital Painting. Computer Graphics. Volume 18, Number 3 July 1984, 245-252.
6. Павлидис Т. Алгоритмы машинной графики и обработки изображения. Перевод с английского: - М., “Радио и связь ” 1986 г., 400 с.
7. Сидорова В.С. Текстурный анализ аэрокосмических изображений на ЭВМ. 30-36.
8. Прэтт У. К., Фожра О. Д., Гагалович А. Применение моделей стохастических текстур для обработки изображений. ТИИЭР 5, 1981, 54-64.
9. Andre Gagalowicz, Sond De Ma, Catherine Tournier-Lasserve 1-D Model for Color Texture. Computer Vision for Robots, 1985 45-49.
10. David D. Garber and Alexander A. Sawchuk, Texture Simulation Using a Best-Fit Model. Pattern Recognition and Image Processing, August 1981, 603-608.
11. Noboru Funakubu Region Segmentation of Biomedical Tissue Image Using Color Texture Feature Pattern Recognition and Image Processing, Juli30 –August 2, vol. 1, 1984, 30-32.
12. Hidefumi Kobatake and Jun Moroo Partition of Texture Image Using Two-Dimensional Linear Prediction Model.

Вверх