

Прокопенко Всеволод Анатольевич
Тема магистерской работы:
Разработка и исследование модема для сверхвысокочастотного радиоканала телекоммуникационной системы.
Научный руководитель: Воронцов А.Г.


|
Прокопенко Всеволод АнатольевичТема магистерской работы: |
| [Назад в библотеку] |
Общая постановка проблемы. Одна из современных тенденций развития телекоммуникационных систем (ТКС) заключается в использовании методов многопозиционной цифровой модуляции (МЦМ) (таких как QAM-256, SSQAM-256 и др.), которые характеризуются расширенным спектром. Обработка таких сигналов, в аппаратуре канала связи (КС), в частности в реальных усилителях мощности (УМ), вызывает определенные проблемы, связанные с расширением спектра и снижением уровня помехоустойчивости. Интермодуляционные искажения сигнала, вызванные оконечным УМ канала передачи ТКС являются одними из основных причин возникновения ошибок в КС [1].
Это явление неприемлемо для современных ТКС, так как спектр сигналов расширяется, что может привести, в условиях ограниченности радиочастотного ресурса [2], к нежелательному наложению спектра одного КС на спектр другого КС.
При проектировании, наладке и эксплуатации систем связи уже давно принято считаться с интермодуляционными компонентами (ИК) второго и третьего порядка, явления связанные с ними уже давно описаны в литературе [3]. Изучение ИК четвертого порядка не актуально т.к. все чаще применяются балансные схемы, исключающие появление четных порядков [4].
Основной задачей данной работы является изучение влияния интермодуляционных искажений пятого порядка на работу ТКС.
Решение задач и результаты исследования. Типичная передаточная характеристика реального УМ имеет вид кривой с участками насыщения. Такую характеристику можно аппроксимировать полиномом n-й степени:
| y = a0 + a1x + a2x2 + a3x3 + a4x4 + a5x5 + ... + anxn. | (1) |
Из соотношения (1) видно, что выходной сигнал усилителя кроме усиленного входного сигнала будет иметь в своем составе множество компонент, из которых интерес представляют ИК пятого порядка.
Пусть входной сигнал состоит из двух косинусоидальных компонент (это могут быть составляющие полезного сигнала либо полезный сигнал и помеха):
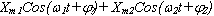
| (2) |
Далее для простоты и наглядности под w1 и w2 будем иметь в виду значения частоты и первоначальной фазы компонент (w1 t+j1 ) и (w2 t+j2 ) , а под X1 и X2 - амплитудные значения Xm1 и Xm2
Известно, что: 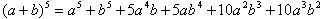
| (3) |
Подставляя вместо a и b компоненты X1Cos(w1 )
и
X2Cos(w2 )
соответственно, преобразовывая функции вида Cosn(w ) к виду Cos(mw ),
вынося за скобки повторяющиеся коэффициенты, упорядочивая члены по частотам, в соответствии с порядком частотной комбинации, получаем выражение:
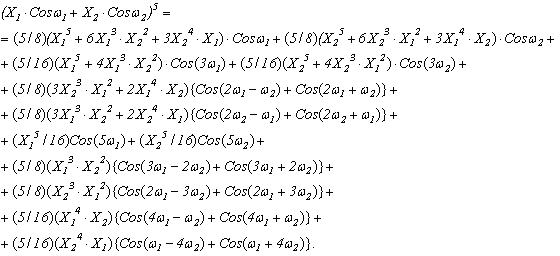
(4)
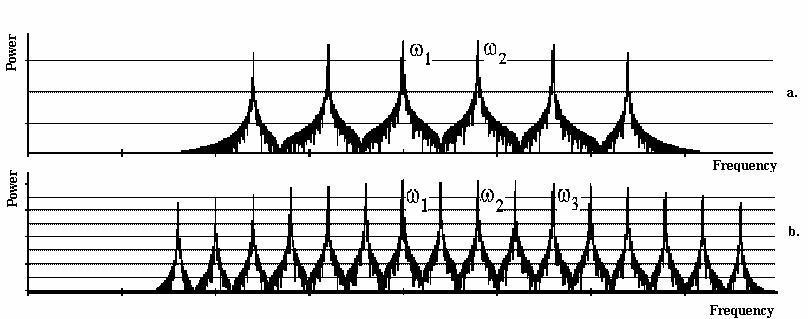
Рис.1. Частотный спектр УМ пятого порядка
При подаче на вход УМ трех компонент с частотами (w1) , (w2) , (w3) спектр сигнала расширяется, появляются ИК лежащие внутри спектра полезного сигнала.(рис1.b). Заметим что на рис1. не показаны два спектральных пучка, для каждого случая аналогичные показанным, которые лежащие в области более высоких частот
Выводы. В спектре выходного сигнала УМ пятого порядка содержится больше ИК компонент, чем в спектре УМ третьего порядка [5]. Спектр его расширяется, это может привести к наложению на спектр других КС. При прохождении через НП широкополосного полезного сигнала, в результате появления ИК лежащих внутри спектра полезного сигнала, может произойти сбой ТКС в результате невозможности выделения полезной информации из выходного спектра.
Уровень высших гармоник (второго и третьего "пучка") отстоит от уровня основного сигнала на 15дБ и 25дБ (соответственно). Учитывая их удаленность по частоте от полезных компонент (ПК) сигнала можно говорить о фильтрации этих гармоник при помощи полосового фильтра без особой сложности.
Переход на современные МЦМ ужесточает требования к степени линейности оконечных УМ канала связи ТКС.
Использованная литература:
1. Triquint Semiconductor GmbH, Konrad-Zuse Platz 1, 81829 Munich, Germany, March 2003y.
2. Кеннет Р. Фостер и Артур В. The Microwave Problem.-Scientific American, Inc. 1986г.
3. Андреев В.С. Теория нелинейных электрических цепей. - М. Связь 1972г.328с
4. http://ru3ga.qrz.ru/UZLY/r180381.htm Andreas Werthof
© Прокопенко В.А., 2007г.