ИСПОЛЬЗОВАНИЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ПРИ СОСТАВЛЕНИИ РАЗДЕЛА «ОРГАНИЗАЦИЯ УПРАВЛЕНИЯ   ПРОИЗВОДСТВОМ» ПРОЕКТОВ УГОЛЬНЫХ ШАХТ

Докт. техн. наук А. С. СТУГАРЕВ, кандидаты техн. наук М. А. БУРШТЕИН, В. И. ДРИГА (ЦНИЭИуголь)

 

В связи с возросшими нагрузками на все технологические звенья, повышением интенсификации и концентрации горных работ в настоящее время все большее значение приобретает проблема создания систем автоматизированного управления угольными шахтами. Согласно СН-202 проекты строительства новых шахт должны включать разделы по организации управления предприя­тием.

Под термином «оперативное управление угольной шахтой» понимается комплекс задач: оптимизация суточных и сменных за-даний (оперативное планирование), составление и контроль графиков организации работ, выработка оптимальных стратегий управления и ежесуточный анализ производственной деятельности основных участков и служб предприятий. Взаимоувязку этих за-дач иллюстрирует схема, приведённая на рисунке. На схеме при-

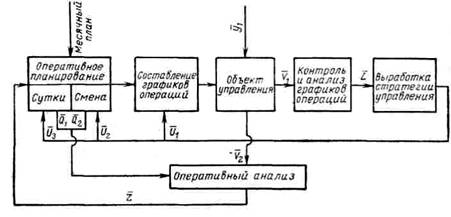
Укрупненная  структурная схема оперативного управления  угольной шахтой

 

няты следующие условные обозначения:

—векторная перемен­ная, характеризующая различные возмущающие воздействия, ко­торые оказывают влияние на функционирование объекта управле­ния;

— векторная переменная, компонентами которой являются величины, характеризующие функционирование объекта управле­ния в течение рассматриваемой смены и учитываемые при выра­ботке оптимальной стратегии управления  в данной смене;

— векторная переменная, компоненты которой характеризуют функ­ционирование объекта в течение текущей смены и суток и учиты­ваются при расчете задания на следующие сутки и смену;

— векторная величина, компонентами которой являются величины рассогласований в выполнении отдельных операций технологиче­ского процесса;

— векторные величины, компоненты ко­торых характеризуютуправляющие воздействия соответственно в течение данной смены, а также    последующих смен и суток;

_, — векторные величины, характеризующие соответственно су­точные и сменные задания;

— векторная величина, компоненты которой характеризуют результаты анализа деятельности рассмат­риваемого участка за прошедшие сутки.

Первым элементом подсистемы оперативного управления для очистных забоев является оперативное планирование. При опре­делении суточных заданий в качестве критерия оптимальности принимаем величину условной прибыли по шахте. Основой расчета является месячный план добычи; при установлении задания очи­стным забоям на текущие сутки учитываются величина ожидаемых простоев, а также разница технико-экономических показателей функционирования каждого из забоев (сдельная расценка за 1 т угля, зольность угля, постоянные затраты на добычу 1 т и пр.); за­траты, непосредственно с добычей не связанные, учитываются по шахте в целом.

Ожидаемую прибыль шахты за принятый период оперативного планирования (месяц) можно представить как

где V — ожидаемая прибыль предприятия на конец месяца;

 — прибыль, полученная    за. рабочих дней,    прошедших с начала месяца;

V_t — прибыль, которая может    быть получена    за t рабочих дней, оставшихся до конца месяца. Задача оптимизации суточных заданий очистным забоям фор­мулируется следующим образом: нужно найти такое распределение заданий по добыче между забоями, которое бы максимизировало ожидаемую прибыль по шахте за оставшиеся    до конца месяца t рабочих дней.

Целевая функция решаемой задачи имеет вид

при ограничениях

 

 

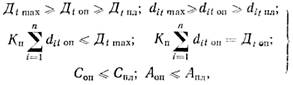
где

d_it — добыча из i-го очистного забоя за время t, т;

i = l, 2, .., n — число очистных забоев на шахте;

Ц — расчетная цена  1 т угля по шахте, руб.;

К_п — коэффициент выхода угля из очистных забоев;

a_1i, a_2i — расчетные коэффициенты, учитывающие основную и дополнительную заработную плату рабочим i-го очистного забоя,  а  также начисления  на  нее,  отнесенные к 1 т добываемого в данном забое угля, руб.;

b_iп — постоянные затраты на 1 т угля в i-м забое, руб.;

S_П — постоянные затраты на  1  т угля  по шахте, руб.;

S_C — постоянные суточные затраты по шахте, руб.;

Д_{t max} — максимальная добыча по шахте за время t, т;

Д_{t оп} — оптимальное задание по шахте на время t, т;

Д_{t пл} — плановая добыча по шахте за время t, т;

d_{it max} — максимальная добыча из i-го забоя за время t, т;

d_{it оп} — оптимальное задание i-му забою на время t, т;

d_{it пл} — плановая добыча из i-го забоя за время t, т;

С_пл, С_оп — соответственно   плановая   и оптимальная   себестоимость 1 т угля по шахте, руб.;

А_пл, А_оп — соответственно   плановая   и   оптимальная   средняя зольность угля по шахте, %.

 

В такой постановке задача сводится к нахождению в выпук­лом многоугольнике решений, определяемом целевой функцией и ограничениями, стационарной точки, в которой достигается мак­симум функции п переменных.

Для решения данной задачи использована одна из модифика­ций градиентного метода. Развитием суточного задания во вре­мени является сменное задание очистным забоям. Необходимо оп­ределить такую структуру нагрузок на забои в данную смену, при которой полученные в результате решения задачи (1), (2) опти­мальные значения суточной добычи, себестоимости и средней зольности по шахте не ухудшатся. Следовательно, ищется не экст­ремальная точка в многоугольнике решений, а любая из стацио­нарных точек, удовлетворяющая принятой системе ограничений.

Развитием сменного задания очистным забоям по добыче в пространстве и времени служит график организации работ. Здесь основным вопросом является установление оптимальной численно­сти комплексной бригады и расстановка рабочих. Экономико-ма­тематическая модель определения оптимального графика   органи зации работ в очистном забое, разработанная докт. эконом, наук А. С. Астаховым и канд. техн. наук  Э. И. Гойзманом,   имеет  вид

 

при ограничениях

где

λ — суммарная  трудоемкость работ в лаве   и обслуживающих лаву смежных   технологических звеньях;

Т — длительность цикла в очистном забое;

Д — добыча угля за один цикл, являющаяся посто­янной для данных условий величиной;

r — количество рабочих смен в сутках;

z — число рабочих в комплексной бригаде;

с — число рабочих «постоянного штата» в лаве и вне ее;

v_i — линейная  скорость  выполнения   i-гo  процесса одним рабочим;

i = l, 2, .., n — номер операции в планограмме работ;

Δ_k — непересекающиеся  отрезки  времени,  на  кото­рые разделена длительность технологического цикла   (операционные состояния);

k = 1, 2, ... — номер операционного состояния;

X_ik — численность звена рабочих, выполняющих i-ю операцию  в течение промежутка  времени Δ_k;

W_i — объем работ за цикл по i-й операции;

X_nk — число рабочих, простаивающих в течение  периода времени Δ_k

a_k — число рабочих, занятых в период времени Δ_k обеспечением работы добычной машины;

l(t_k) — путь,  пройденный  добычной  машиной  за  вре­мя t_k;

d — критическое   расстояние   между   местами   вы­полнения двух процессов;

T_р — суммарная    длительность    рабочих     смен    в сутки;

Q — суточное  задание  по добыче  угля  из  данного забоя;

 

Для решения задачи могут быть использованы методы спуска, которые приводят к локальному минимуму. Однако в данном слу­чае абсолютный и локальный минимумы будут эквивалентны, по­этому полученное решение является оптимальным.