Наукові праці Донецького Національного Технічного Універсітету Серія: «Обчислювальна техніка та автоматизація» вип. 107. – с. 56-61.
ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СВОЙСТВ РЕКУРРЕНТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Воронцов А.Г., Синельников В.Б.
Донецкий национальный технический университет, г. Донецк
кафедра автоматики и телекоммуникаций
E-mail: vag@fcita.dn.ua
Abstract Vorontsov O.G., Dorovikov D.A., Sinelnikov V.B. Investigation Dynamic Properties of Recurrent Fourier Transform. Estimation of transition time the recurrent spectrum generating and estima-tion of magnitude spectrum error are determined. Computer simulation of action the recurrent Fourier analyzer is adduced.
Общая постановка проблемы. Рекуррентное преобразование Фурье (РПФ) как метод получения оценки текущего спектра сигнала с помощью цифровых вычислителей впервые предложен в [1,2] и разрабатывалось в основном для нужд синтетической телефонии. Известно так же предложение использовать его в радиолокационных системах [3]. Однако сведения о динамических погрешностях оценок при воспроизведении текущего спектра сиг-нала отсутствуют, что ограничивает возможности его применения в измерительных системах.
Основной задачей данной работыявляется исследование динамических свойств РПФ, определяющих погрешности оценок текущих спектров сигналов.
Решение задач и результаты исследования.Комплексный текущий спектр искретного по времени комплекснозначного сигнала:
ý(k)=a(k)+jb(k),
где K=0,1,2... идентификатор номера отсчета в дискретном времени, может быть определен по формуле, полученной из [4]
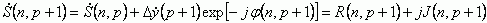 |
(1) |
где Δý(p+1)= ý(p+1) - ý(p+1-N) для P≥N-1;
и Δý(p+1)= ý(p+1) для Р< N-1;
N - размер выборки;
P=0,1,2,... - идентификатор номера выборки;
φ=(n,p+1)=2πn(p+1)/N - значение фазы n--й базисной функции для p+1й выборки;
n=0,1,2...,N/2-1- идентификатор номера базисной функции;
R(n,p+1)=R(n,p)+Y(p+1)sinφ(n, p+1) |
(2a) | J(n,p+1)=J(n,p)+Y(p+1)cosφ(n, p+1) |
(2б) |
Y(p+1)=[a(p+1)+b(p+1)-a(p+1-N)-a(b+1-N)] для P≥N-1; | |
и Y(p+1)=a(p+1)+b(p+1) для P< N-1; |
Фактически РПФ осуществляет вычисление оценок спектральных линий дискретного преобразования Фурье в скользящей системе отсчета связанной с последними отсчетами, размещаемыми в регистровой памяти, объемом в ячеек. Для большинства приложений практический интерес представляет динамический спектр амплитуд
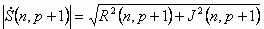 |
(3) |
Если при выполнении рекурсии (1а,б), начиная с некоторого, выполняются условия
R(n,p+1)=R(n,p) J(n,p+1)=J(n,p) |
(4) |
процесс последовательного уточнения n-й спектральной линии заканчивается.
Пусть процесс ý(k) отображает скачек на n-м отсчете:
ý(k)=1(n-k)(ao+jbo) |
(5) |
где 1(n) - единичная ступенчатая функция.
В этом случае эквивалентом условия (4) являются равенства
a(p+1)=a(p+1-N) b(p+1)=b(p+1-N) |
которые начинают выполняться с момента поступления на вход регистровой памяти N отсчетов скачка. Поступление дополнительных отсчетов сверх этих N не изменяет результата вычислений ни для одной из N/2спектральных линий, формируемых анализатором, так как величина Y(p+1), входящая в рекурсии (2а,б), для любого p < N-1 и для любого 0≤n≤N/2-1 остается неизменной.
На основании вышеизложенного, а так же учитывая линейность соотношений (2а,б) по отношению к анализируемому сигналу можно прийти к заключению, что всякое изменение в поведении сигнала ý(k)=a(k)+jb(k), на k-м отсчете адекватно отображается в спектре, вычисляемом анализатором на (k+N)-м отсчете и таким образом время, затрачиваемое анализатором на обработку N отсчетов, определяет запаздывание вносимое анализатором. Но с другой стороны, следует учитывать, что N определяет число спектральных линий, формируемых анализатором, и значение этой величины предопределяется требованиями решаемой технической задачи. Значение величины шага дискретизации tд определяется верхней границей спектра исследуемого процесса и также не может быть выбрано произвольно. Таким образом, если значения N и tд заданы внешними условиями, запаздывание в выдаче результатов анализа может быть оценено как
τ≥Ntд |
Окончание процесса уточнения уровня компонент спектра за конечное число шагов рекурсии равное N приводит к появлению неустранимой составляющей методической ошибки. Оценку этой ошибки можно получить, рассмотрев процесс формирования результатов вычисления спектра на ограниченном интервале, соответствующем N отсчетам и для случая, когда этот интервал не ограничен.
Для упрощения анализа будем считать, что анализатор формирует текущий спектр скачка (5) при нулевых начальных условиях:
|
ý(k)=a(k)+jb(k), R(n,0)=0 J(n,0)=0 |
(6) |
С учетом вышеуказанных условий, при любом значении справедливо равенство Y(p+1)=ao+jbo=Yo=const. Тогда из соотношений (2а,2б) получим
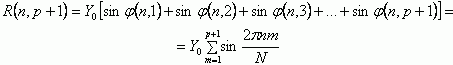 |
(7а) |
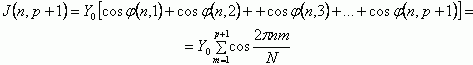 |
(7б) |
Комплексный текущий спектр для рассматриваемого случая равен
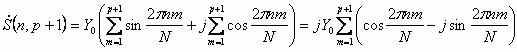 |
(8) |
После очевидных преобразований выражение (8) приобретает вид
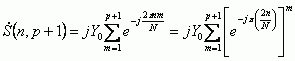 |
(9) |
Вычислив значение суммы, воспользовавшись правилам суммирования слагаемых геометрической прогрессии [5], получим
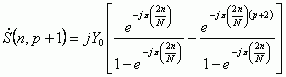 |
(10) |
Оценка спектра, формируемая рекуррентным анализатором непосредственно после поступления N-1-го отсчета, является наилучшим приближением к спектру неограниченного по времени сигнала (6).Более точный результат может быть получен при расширении объема регистровой памяти, что связано с требованием увеличения размера выборки N. При неограниченном увеличении N получим
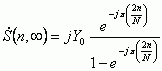 |
(11) |
Разница между (11) и (10) для p=N-1 дает комплексный спектр соответствующий погрешности оценки в сравнении с воспроизведением спектра неограниченного по длительности сигнала (6) рекуррентным анализатором
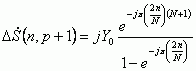 |
(12) |
Подтверждение приведенных результатов, а так же новые результаты были получены при исследовании динамических свойств рекуррентного анализатора в процессе вычисли-тельного эксперимента. Программа, осуществляющая вычисление текущего спектра ампли-туд тестового сигнала реализована на языке С++ 3.0. В качестве тестового сигнала выбран гармонический сигнал с частотой 1 Гц, нулевой начальной фазой и единичной амплитудой, помноженный на единичную ступенчатую функцию. Тестовый сигнал задается дискретно. Частота дискретизации составляет 8 Гц. Нулевой отсчет совпадает с нулем осей времени, частоты и уровня на трехмерных графиках текущих спектров. В зависимости от протяжен-ности переходного процесса становления текущего спектра обрабатывались от 192 до300 от-счетов. Размерность базового преобразования Фурье - 128 отсчётов. Результаты экспери-ментов в виде трехмерных графиков приведены на рис. 1-4.
Как видно из рис.1 установление уровня спектральной линии, отображающей гармоническую составляющую тестового сигнала, происходит по закону близкому к линейному и полностью заканчивается за N=128 отсчетов. На графике это соответствует началу первого участка стабилизации уровня основной спектральной линии и резкому уменьшению пере-ходных компонент (фона) текущего спектра. Уменьшение уровня переходных компонент после обработки N-го отсчета составляет значительную величину (120-150дБ).
Скачек фазы анализируемого тестового сигнала после установления уровня оцениваемой спектральной компоненты приводит к новому переходному процессу становления спектра, который занимает интервал протяженностью в N отсчетов. В переходном процессе уровень основной спектральной линии снижается, а затем возрастает до первоначального уровня. Значение уменьшения уровня определяется значением скачкообразного приращения фазы тестового сигнала. При скачках фазы близких к ±π уровень основной спектральной линии может оказаться ниже уровня «фона» (рис. 2). Однако и в этом наиболее сложном случае переходный процесс становления спектра заканчивается ровно за N отсчетов.
Скачки фазы тестового сигнала, следующие до окончания переходного процесса от ранее действовавшего возмущения, затягивают переходный процесс становления спектра. Он заканчивается по прошествии отсчетов с момента начала действия последнего возмущения (рис.3 и рис.4).

Рисунок 1 - Текущий спектр амплитуд тестового сигнала, включаемого на нулевом отсчете и последующим скачком фазы в 60 градусов на 135 м от-счете.

Рисунок 2 - Текущий спектр амплитуд тестового сигнала, включаемого на нулевом отсчете и последующим скачком фазы в 180 градусов на 135 м отсчете.

Рисунок 3 - Текущий спектр амплитуд тестового сигнала, включаемого на нулевом отсчете и последующими скачками фазы на 135-м отсчете (68 градусов) и 160-м отсчете (122 градуса).

Рисунок 4 - Текущий спектр амплитуд тестового сигнала, включаемого на нулевом отсчете и последующим скачком фазы в 60 градусов на 64 -м отсчете.
Выводы
- Динамические свойства рекуррентного Фурье-анализатора определяются числом ячеек регистровой памяти анализатора N и частотой дискретизации. Переходный процесс становления текущего спектра сигнала после воздействия элементарного возмущения закан-чивается за интервал времени соответствующий Nотсчетам временной дискретизации.
- В момент окончания переходного процесса резко уменьшается уровень переходных компонент (фона) текущего спектра. Однако завершение вычисления спектра любого явле-ния в сигнале за конечное число итераций может быть причиной накопления погрешностей спектральных оценок. Величина погрешности уменьшается с увеличением N.
- При считывании данных с анализатора до завершения процесса становления спектра следует принимать во внимание дополнительную погрешностью вычисления уровней оцениваемых спектральных компонент (недовычисление уровней) и фон текущего спектра.
Литература
- Лейтес Р.Д., Соболев В.Н. Цифровое моделирование систем синтетической телефонии.-М.: Связь, 1969.-120с.
- Чайковский В.И., Коваль В.Ф., Краковский В.Я. Анализатор спектра Фурье. АС №560232 СССР. Опубл. 1977, Бюл. №20.
- Устройство для вычисления дискретного «скользящего» преобразования Фурье и его применение в радиолокационной системе. Заявка №0207859 Франция. – Опубл. Изо-бретения стран мира, 1987. -№17.-Вып.17.
- Плотников В.Н., Белинский А.В., Суханов В.А., Жигулевцев Ю.Н. Цифровые анали-заторы спектра.- М.: Радио и связь, 1990. – 184с.
- Воробьев Н.Н. Теория рядов.- М.: Наука, 1975. – 368с.