МЕТОД ФОРМИРОВАНИЯ АМПЛИТУДНОГО И ЭНЕРГЕТИЧЕСКОГО ДИНАМИЧЕСКИХ СПЕКТРАЛЬНЫХ СОСТОЯНИЙ
В ЕДИНОЙ СТРУКТУРЕ
БЕЛИНСКИЙ А. В., МАШКОВ В. В., ПЛОТНИКОВ В. Н.
(Москва)
Источник: журнал «Автоматика и телемеханика» 1982 г. №8, с. 145-151.
Рассматриваются виды формирования амплитудного и энергетического динамических спектральных состояний в обобщенных рекуррентных структурах, сходные по алгоритмической реализации, с целью увеличения производительности аппаратуры
Формирование динамического спектрального состояния (ДСС) как пошаговой процедуры отображения входной дискретной последовательности в частотной области в качестве амплитудного, фазового, энергетического и других состояний довольно трудоемко в смысле затрат на вычислительные операции. Однако ряд исследований [1,2] показывает, что ДСС весьма полезно с точки зрения обработки сложных сигналов, так как дает возможность их полного и всестороннего анализа. Большая размерность объема вычислений при динамической спектральной обработке в цифровом виде приводит к ограничению числа наблюдаемых спектральных состояний особенно при требованиях работы в темпе с процессом. В широких интервалах N исходной выборки f данная задача для ДСС даже при использовании высокоэффективных алгоритмов быстрых спектральных преобразований [3 — 5] не может быть решена в реальном масштабе времени уже для диапазона квантования поступающей входной последовательности более десяти килогерц без существенного наращивания аппаратных мощностей. Так при N=128 c применением быстрого преобразования Фурье (БПФ) в скользящем режиме для уровня квантования десять килогерц потребуется около 45 × 106 операции типа алгебраического сложения в секунду.
В работе дается метод формирования динамического комплексного амплитудно-частотного п динамического энергетического спектральных состояний (ДЭСС), увязанный в одну рекуррентную процедуру с, целью увеличения производительности аппаратуры и расширения диапазона ограничений на данный вид спектральной обработки.
Обладая существенной избыточностью в своем полном объеме, динамические спектральные состояния входной дискретной последовательности обладают и тем важным качеством, что дают возможность выделения таких параметров, которые иными путями получаются либо со значительно большими по сложности обработки затратами, либо вообще недостижимы.
Рассмотрим формирование ДЭСС. Ввиду существенного объема вычислительных операций при прямом применении формы определения энергетического спектра в динамической пошаговой обработке представляется необходимым получить рекуррентную процедуру формирования ДЭСС. Под рекуррентной процедурой будем понимать форму алгоритмического обеспечения, когда последующее спектральное состояние формируется не на основе исходной дискретной выборки входного сигнала, а на основ предыдущего спектрального состояния.
Пусть спектральная плотность мощности (СПМ) определена в виде (автоэнергетический спектр):
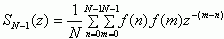 |
(1) |
где z - комплексная переменная; N - ограниченная размерность выборки ограниченных дискретных значений входной последовательности f(n); f(m) определяет автопреобразование для f(n). Тогда при смещении выборки на одно дискретное значение в окне наблюдения текущей дискретной последовательности исходного сигнала СПМ новой совокупности будет:
 |
(2) |
Определим (2) через (1). Нормирование 1/N для простоты в дальнейших выкладках опустим:
 |
(3) |
где запись {•} есть повторение предыдущих фигурных скобок; df=f(N)-f(0), т.е. исключается влияние пулевого дискретного значения f(0) и учитывается дополнение отсчетом f(N)
Динамическая спектральная обработка подразумевает пошаговую процедуру отображения исходного сигнала в частотной области, однако, зачастую требуется на отдельных участках обрабатываемого сигнала (участки квазистационарности, функциональной определенности и т. д.) реализовывать скачущее применение алгоритма. Получим обобщенное рекуррентное ДЭСС при произвольном шаге выборки tш, но при неизменной дискретизации. Для этого целесообразно представить индукцию вывода.
Пусть t=2, тогда
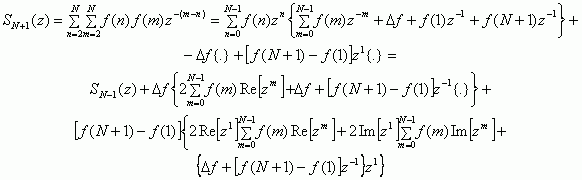 |
При t=3, проделав аналогичные преобразования, получим:
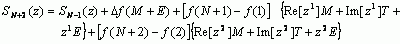 |
|
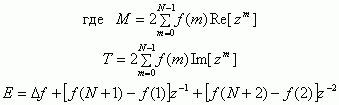 |
Таким образом. можно записать рекуррентное соотношение для произвольного шага tш ДЭСС:
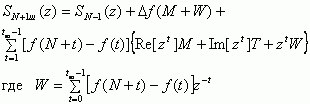 |
Если ДЭСС или динамическую СПМ реализовать на единичной окружности, то для пошаговой процедуры (скользящей) соотношение (3) примет вид:
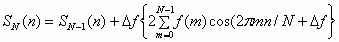 |
(4) |
Вывод: при пошаговой реализации (1) для целей динамической СПМ с каждым вновь приходящим дискретным значением необходимо выполнить 3N2 операций умножения при действительном f. Организуя вычислительный процесс, но рекуррентной процедуре вида (3), для получения последующей СПМ нужно выполнить (N+1)N операций умножения. Уменьшается также и число операции типа алгебраического сложения
Однако формула (4) оказывается приемлемой в наилучшем смысле только в организации формирования обобщенной структуры ДСС. При получении только ДЭСС более эффективно другое соотношение.
Расписав почленно (1) и объединив члены с одинаковой степенью z, получим формулу для СПМ:
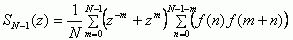 |
(5) |
Выразим SN(z) через (5). В этом случае (нормирование опустим):
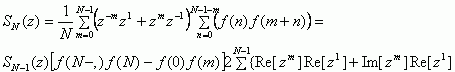 |
(6) |
Рекуррентное соотношение (6) па единичной окружности станет:
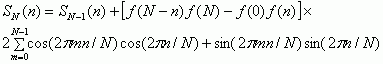 |
(7) |
Сравнивая (7) с (4), можно отметить, что если в (4) выражение и фигурных скобках содержит элементы f, которые неизвестны системе обработки до своего поступления, то в (7) выражение в фигурных скобках может быть заранее вычислено и занесено в матрицу констант организации вычислений. Следовательно, для рекуррентной процедуры (7) при формировании последующего ДЭСС из предыдущего нужно провести лишь 3N операции умножения. Это указывает на предпочтение (7) перед (4) в реализации только ДЭСС.
Но в исполнении (7) есть и отрицательное качество: наряду с увеличением быстродействия аппаратуры увеличивается и объем аппаратных средств, что в ряде случаев нежелательно.
Рассмотрим формирование рекуррентного комплексного амплитудно-частотного спектра (АЧС). Представив дискретное преобразование Фурье в виде:
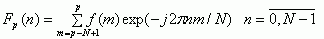 |
(8) |
Для t=1 получим следующее выражение:
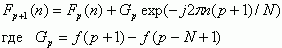 |
(9) |
При произвольном tш, исходя из (8), обобщенная рекуррентная формула имеет вид:
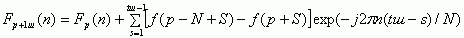 |
(10) |
Следует заметить, что представленное в [6] выражение для рекуррентного АЧС: Fp+1(n)=exp(jω1)|Fp(n)+Δf| или в более общем виде для произвольного tш (получено авторами):
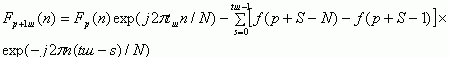 |
(11) |
имеет ряд существенных недостатков по сравнению с (10): накопление ошибки рекуррентной процедуры (11) происходит достаточно быстро и она не детерминирована, так как зависит от случайного генерирования пака погрешности при вычислении тригонометрических величин; выражение (11) требует в два раза больше операции умножения но по сравнению с (10); выражение (11) неконструктивно в смысле удобства н эффективности проектирования на его основе специализированной аппаратуры.
Рассмотрим вопрос накопления погрешности рекуррентных процедур (10) и (11) для случая t=1
Получение комплексных значения для (10) происходит по соотношениям:
 |
(10а) |
А получение комплексных значении в (11) будет реализовываться как:
 |
(11а) |
где A(n)=Re[Fp(n)]+Δf; B(n)=Im[Fp(n)]
Пусть вычисление производится на цифровой вычислительной машине общего назначения. Основная погрешность вычислительных процедур будет обусловлена усечением счетного ряда и пакете стандартной подпрограммы для тригонометрических функций. Остальные значения могут быть представлены практически с неограниченной точностью.
Запишем значения cos(2 π/N) и sin(2 π/N) в виде с±ε и d±ε соответственно, где c, d - точные значения косинуса н синуса, а ε - ошибка определения тригонометрических функций. Получим общую структуру полинома при ошибке ε1.
Полином р-го шага для (11а) будет:
 |
(соответствующий полипом р-го шага), где Δfsub>1=f(N)-f(0); Δf2=f(N+1)-f(1);…; Δfp=f(N+1)-f(p)
Для соотношения (10а) выражение формирования полинома перед ε1 определится как:
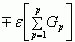 |
Пусть c=0,8; d=0,36 все значения f равны fmax тогда (10а), сравнительно с (11а) по максимальной положительной ошибке ε1 в числовых значениях, станет пошагово (четыре шага):

Таким образом, указанный недостаток (11) по накоплению ошибки рекуррентной процедуры справедлив.
Следует заметить, что формулы (10) и (11) не эквивалентны в комплексном виде. Они определяют одинаковый АЧС в виде модулей комплексных коэффициентов Фурье, что здесь и обсуждается. Истинный комплексный спектр определяет только (11).
Сравнение рекуррентных формул для целен формирования ДСС в виде АЧС с другими алгоритмами быстрого получения коэффициентов Фурье основывается главным образом па интервале между двумя обработками. Существует определенная граница скачка (интервала между двумя спектральными грезами, выраженного в единицах числа дискретных значений), для которой число операций при использовании рекуррентных формул и других алгоритмов, например БПФ, приблизительно равно.
В таблице показано количество операций умножения для различных N алгоритма БПФ (число операции умножения для БПФ взято равным Nlog2N) рекуррентной формулы (10) при различных t без оптимизации вычислительного процесса. Граница равных затрат выделена жирной линией.
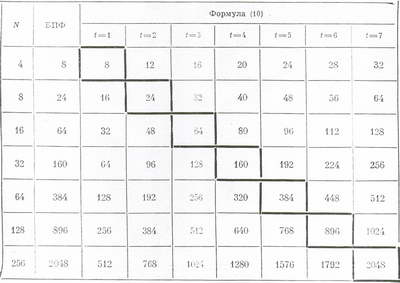
Выберем за основу формирования АЧС формулу (9). Основным действием, в (9) является умножение циклических по р констант Gp на cos(2 π (p+1)/N). Так как величина Gp неизменна по шагу р, то отпадает необходимость умножения на синус; результаты умножения на косинус переприсваиваются но массивам в универсальном исполнении или коммутируются при спецпроцессорной реализации. Достаточность информации по умножению на косинус заключена в четверти периода. Организация вычислений осуществляется по принципу умножения числа на табличные константы. Используя командные языки программирования, целочисленное представление всех величин (с оговорками на достигаемую точность), оптимизацию за счет двоичной избыточности матрицы констат, удается повысить производительность аппаратуры на два и более порядка по сравнению с обычным программным обеспечением.
Пример. Покажем реализацию способа оптимизации умножения числа табличные константы за счет двоичной избыточности.
Пусть N=16. Достаточность информации для N=16 заключена в умножении Gp па косинусы π/8, π/4, Зπ/8. Обозначим мантисы косинусов через x. В восьмиразрядном виде представления они будут:
x(2)=01011010,
x(3)=01100001
Отсюда очевидно, что в комбинациях нулей-единиц присутствуют одинаковые сочетания для трех констант. Следовательно, очевидным является то, что эффективно использовать результат умножения Gp на исходное сочетание в произведении Gpx(1) для определения результатов Gpx(2) и Gpx(3)
Пусть для рассматриваемой совокупности этим сочетанием является 11. В этом случае умножение Gp на табличные константы можно осуществить по алгоритму:
|
m1=Gp2-1+Gp, (1)=(m1+Gp2-1+m12-4)2-1, (2)=(Gp+m12-1+Gp2-5)2-1, (3)=Gp+m12-5, |
(12) |
где 2-1 условный сдвиг влево; m1, — значение Gp, умноженное на 11; (1) - результат Gpx(1); (2) - Gpx(2); (3) - Gpx(3).
Соотношение (12) требует значительно меньшого количества элементарных операций (сложения, сдвига, перехода), чем обычное умножение Gp константы х.
Отметим, что существенное внимание должно уделяться в данном способе умножения выбору базового сочетания нулей и единиц в табличных константах. Обычно существует несколько вариантов формирования структуры типа (12), потому необходим анализ по выбору из совокупности наилучшего.
Сравним формирование амплитудного и энергетического ДСС (9) и (4) в плане выполнения их на единой структуре. Если (4) представить как
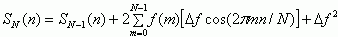 |
то, использовав результат умножения Δfcos(2πmn/N) в формировании ДЭСС, для динамического АЧС, достаточно 2N алгебраических сложении при получении АЧС последующего состояния из предыдущего.
Разработанный метод формирования и единой рекуррентной структуре динамического энергетического н динамического амплитудно-частотного состояний дает возможность значительно уменьшить объем вычислений в данном виде обработки и представляет интерес в радиолокации, цифровой обработке речевых сигналов, обработке изображения, гидроакустике и других областях.
Литература
- Файн В. С, Опознавание изображений. М.: Наука. 1970.
- Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. М.: Мир, 1978.
- Бергланд Дж. Д. Руководство к быстрому преобразованию Фурье. — Зарубежная радиоэлектроника, 1971, № 3 с 52-72.
- Гоулд Б., Рейдер Ч. Цифровая обработка сигналов. М.: Советское радио, 1973.
- Алгоритмы быстрого преобразования Фурье и их свойства.— Зарубежная радиоэлектроника, 1979, № 2 с 3-29.
- Лейтес Р. Д., Соболев В. НI. Цифровое моделирование систем синтетической теле¬фонии. М.: Связь 1969.