МОДЕЛЬ РАВНОВЕСИЯ С ФУНКЦИЕЙ СПРОСА
ТИПА КОББА-ДУГЛАСА
Источник: http://ipian.kazan.ru/science/sbornik6.html
Введение
В работе
рассматривается модель экономического равновесия в условиях совершенной
конкуренции, в которой рассматривается рынок ![]() типов товаров, а
интересы потребителей определяются функциями полезности типа Кобба-Дугласа. Мы
покажем, что соответствующая задача равновесия может быть сформулирована в виде
смешанного вариационного неравенства: найти точку
типов товаров, а
интересы потребителей определяются функциями полезности типа Кобба-Дугласа. Мы
покажем, что соответствующая задача равновесия может быть сформулирована в виде
смешанного вариационного неравенства: найти точку ![]() такую, что
такую, что
![]()
![]() , (1)
, (1)
где ![]() – выпуклая, но
необязательно дифференцируемая функция,
– выпуклая, но
необязательно дифференцируемая функция, ![]() – некоторое
отображение,
– некоторое
отображение, ![]() – непустое выпуклое подмножество
– непустое выпуклое подмножество ![]() ,
, ![]() неотрицательный
ортант в
неотрицательный
ортант в ![]() .
.
Задача вида (1)
ранее изучалась многими авторами в связи с ее многочисленными приложениями в
математической физике (см., например, [1], [2]). Она совпадает с обычным
вариационным неравенством, если ![]() . Большинство работ
посвящено случаю, когда
. Большинство работ
посвящено случаю, когда ![]() – строго (сильно)
монотонное отображение. Это свойство позволяет получить результаты существования
и единственности решения для задачи (1) и предложить различные методы решения при
достаточно общем виде множества
– строго (сильно)
монотонное отображение. Это свойство позволяет получить результаты существования
и единственности решения для задачи (1) и предложить различные методы решения при
достаточно общем виде множества ![]() .
.
Данная работа
посвящена экономическим приложениям задачи (1). Обычно при этом допустимое
множество ![]() имеет вид конуса или порядкового отрезка.
Показано, что в формулировке вида (1) задачи экономического равновесия
отображение
имеет вид конуса или порядкового отрезка.
Показано, что в формулировке вида (1) задачи экономического равновесия
отображение ![]() имеет тип P, т.е. оно обладает свойствами порядковой, а не обычной
монотонности. Подобные задачи экономического равновесия в условиях совершенной
и несовершенной конкуренции исследовались в [3]. Полученные свойства позволяют
установить ряд новых результатов существования и единственности решений и
применить для их нахождения подход, основанный на
имеет тип P, т.е. оно обладает свойствами порядковой, а не обычной
монотонности. Подобные задачи экономического равновесия в условиях совершенной
и несовершенной конкуренции исследовались в [3]. Полученные свойства позволяют
установить ряд новых результатов существования и единственности решений и
применить для их нахождения подход, основанный на ![]() -интервальных
функциях, который был предложен для таких задач в [4]. Этот подход состоит в
преобразовании задачи (1) в задачу нахождения стационарной точки дифференцируемой
функции. В результате решение исходной задачи можно найти с помощью обычных
методов дифференцируемой оптимизации, таких как градиентный метод и метод
сопряженных градиентов.
-интервальных
функциях, который был предложен для таких задач в [4]. Этот подход состоит в
преобразовании задачи (1) в задачу нахождения стационарной точки дифференцируемой
функции. В результате решение исходной задачи можно найти с помощью обычных
методов дифференцируемой оптимизации, таких как градиентный метод и метод
сопряженных градиентов.
Вспомогательные результаты
Рассмотрим вначале общее смешанное вариационное неравенство (1) при следующих предположениях:
(A1) Отображение ![]() непрерывно на
множестве
непрерывно на
множестве ![]() ;
;
(A2) Функция ![]() имеет вид:
имеет вид: 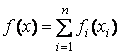 , где
, где ![]() – выпуклая непрерывная
функция для каждого
– выпуклая непрерывная
функция для каждого ![]() ;
;
(A3) Множество ![]() имеет вид
параллелепипеда, т.е.
имеет вид
параллелепипеда, т.е.  где
где ![]() для каждого
для каждого ![]() .
.
Эти предположения
будут считаться выполненными в данном разделе. Из (А3) следует, что ![]() – непустое,
выпуклое и замкнутое множество. Если
– непустое,
выпуклое и замкнутое множество. Если ![]() и
и ![]() для
для ![]() , то
, то ![]() , следовательно,
задача (1) эквивалентна задаче дополнительности с многозначным основным
отображением
, следовательно,
задача (1) эквивалентна задаче дополнительности с многозначным основным
отображением ![]() Здесь и далее
Здесь и далее ![]() обозначает субдифференциал
функции
обозначает субдифференциал
функции ![]() .
.
Для получения результатов существования и единственности решения нам потребуются следующие определения.
Определение
1 (см.,
например, [5], [6]). Квадратная матрица ![]() порядка
порядка ![]() называется:
называется:
a) ![]() -матрицей, если все её главные миноры положительные;
-матрицей, если все её главные миноры положительные;
b) ![]() -матрицей, если все её главные миноры
неотрицательные;
-матрицей, если все её главные миноры
неотрицательные;
c) ![]() -матрицей, если все её внедиагональные элементы
неположительны;
-матрицей, если все её внедиагональные элементы
неположительны;
d) ![]() -матрицей, если все её внедиагональные элементы
неположительны, и обратная матрица
-матрицей, если все её внедиагональные элементы
неположительны, и обратная матрица ![]() существует и имеет
неотрицательные элементы;
существует и имеет
неотрицательные элементы;
e) ![]() -матрицей, если она одновременно является
-матрицей, если она одновременно является ![]() - и
- и ![]() -матрицей.
-матрицей.
Следующее
утверждение является критерием для матрицы ![]() быть
быть ![]() - или
- или ![]() -матрицей.
-матрицей.
Предложение
1 (см.,
например, [6]). Предположим, что ![]() есть
есть ![]() -матрица. Если
существует вектор
-матрица. Если
существует вектор ![]() такой, что
такой, что ![]() (соответственно,
(соответственно, ![]() ), то
), то ![]() есть
есть ![]() -матрица (соответственно,
-матрица (соответственно, ![]() -матрица).
-матрица).
Эти свойства нетрудно обобщить на случай нелинейных отображений.
Определение
2. Пусть ![]() выпуклое
подмножество
выпуклое
подмножество ![]() . Отображение
. Отображение ![]() называется
называется
a) ![]() -отображением [7], если
-отображением [7], если ![]() для всех
для всех ![]() ,
, ![]() ;
;
b) строгим ![]() -отображением [4], если существует число
-отображением [4], если существует число ![]() такое, что
такое, что ![]() есть
есть ![]() -отображение (здесь
-отображение (здесь ![]() есть единичная
матрица порядка n);
есть единичная
матрица порядка n);
c) ![]() -отображением [7], если для всех
точек
-отображением [7], если для всех
точек ![]() ,
, ![]() , существует индекс
, существует индекс ![]() такой, что
такой, что ![]() и
и ![]() .
.
Если ![]() аффинно, т.е.,
аффинно, т.е., ![]() , то
, то ![]() есть
есть ![]() -отображение (
-отображение (![]() -отображение) тогда
и только тогда, когда
-отображение) тогда
и только тогда, когда ![]() есть
есть ![]() -матрица (
-матрица (![]() -матрица). В общем
нелинейном случае, если
-матрица). В общем
нелинейном случае, если ![]() есть
есть ![]() -матрица для любого элемента
-матрица для любого элемента ![]() , то
, то ![]() есть
есть ![]() -отображение, но обратное утверждение в
общем случае неверно. В то же время,
-отображение, но обратное утверждение в
общем случае неверно. В то же время, ![]() есть
есть ![]() -отображение тогда и
только тогда, когда
-отображение тогда и
только тогда, когда ![]() есть
есть ![]() -матрица. Кроме
того, если
-матрица. Кроме
того, если ![]() есть строгое
есть строгое ![]() -отображение, то
-отображение, то ![]() есть
есть ![]() -матрица (см. [4], [7], [8]).
-матрица (см. [4], [7], [8]).
Установим
зависимость между ![]() -отображением и
строгим
-отображением и
строгим ![]() -отображением.
-отображением.
Лемма
1 (см.
[3], лемма 3.6). Если ![]() есть
есть ![]() -отображение и
-отображение и ![]() , то
, то ![]() строгое P-отображение.
строгое P-отображение.
Напомним определения
свойств монотонности для отображений. Для множества S обозначим через ![]() совокупность всех
подмножеств множества S.
совокупность всех
подмножеств множества S.
Определение
3 (см.,
например, [2], [9], [10]). Пусть
![]() выпуклое подмножество в
выпуклое подмножество в ![]() . Отображение
. Отображение ![]() называется
называется
a) сильно монотонным с
константой ![]() , если для любых
, если для любых ![]() и
и ![]() ,
, ![]() , выполняется
, выполняется ![]() ;
;
b) строго монотонным, если для любых ![]() ,
, ![]() и
и ![]() ,
, ![]() выполняется
выполняется ![]() ;
;
c) монотонным, если для любых ![]() и
и ![]() ,
, ![]() выполняется
выполняется ![]() .
.
Заметим, что если
однозначное отображение ![]() монотонно
(соответственно, строго монотонно, сильно монотонно), то оно является
монотонно
(соответственно, строго монотонно, сильно монотонно), то оно является ![]() -отображением
(соответственно,
-отображением
(соответственно, ![]() -отображением, строгим
-отображением, строгим ![]() -отображением), но
обратные утверждения в общем случае неверны.
-отображением), но
обратные утверждения в общем случае неверны.
Далее напомним определения свойств выпуклости функций.
Определение
4 (см.,
например, [11]) Функция ![]() называется
называется
a) сильно выпуклой с константой ![]() , если для любых
, если для любых ![]() и
и ![]() , выполняется
, выполняется
![]() ;
;
b) строго выпуклой, если для любых ![]() ,
, ![]() и
и ![]() , выполняется
, выполняется
![]() ;
;
c) выпуклой, если для любых ![]() и
и ![]() выполняется
выполняется
![]() .
.
Приведем известные соотношения между свойствами выпуклости функций и свойствами монотонности их субдифференциалов.
Лемма
2 (см.,
например, [11]). Функция ![]() является
является
a) выпуклой тогда и только тогда, когда отображение ![]() монотонно;
монотонно;
b) строго выпуклой тогда и только тогда, когда отображение ![]() строго монотонно;
строго монотонно;
c) сильно выпуклой с константой ![]() тогда и только
тогда, когда отображение
тогда и только
тогда, когда отображение ![]() сильно монотонно с
константой
сильно монотонно с
константой ![]() .
.
Нам потребуются некоторые общие результаты существования и единственности решений задачи (1). Рассмотрим случай, когда множество K ограничено.
Предложение 2 ([3], предложение 4.2). Если множество K ограничено, то задача (1) имеет решение.
Теперь приведём
результаты существования и единственности решений из [3] для случая, когда ![]() есть
есть ![]() -отображение.
-отображение.
Предложение
3. a) ([3], теорема 4.4) Пусть
![]() есть
есть ![]() -отображение. Если
функции
-отображение. Если
функции ![]() строго выпуклые для
строго выпуклые для
![]() то задача (1) не может иметь более одного
решения.
то задача (1) не может иметь более одного
решения.
b) ([3], теорема 4.6.) Пусть ![]() есть
есть ![]() -отображение. Если
функции
-отображение. Если
функции ![]() сильно выпуклые для
сильно выпуклые для
![]() то задача (1) имеет
единственное решение.
то задача (1) имеет
единственное решение.
Из предложений 2 и 3a получаем следующее утверждение.
Следствие 1. Если дополнительно к условиям предложения 3а множество K ограничено, то задача (1) имеет единственное решение.
Для индексного
множества ![]() мы будем обозначать
мы будем обозначать ![]() и
и ![]() . Значит,
. Значит, ![]() Обозначим через
Обозначим через ![]() единичную матрицу
порядка
единичную матрицу
порядка ![]() .
.
Предложение
4 ([3],
теорема 4.7). Пусть ![]() дифференцируемое
дифференцируемое ![]() -отображение.
Предположим, что для каждого
-отображение.
Предположим, что для каждого ![]() ,
, ![]() есть
есть ![]() -матрица, и существует
-матрица, и существует
![]() такое, что
такое, что ![]() есть
есть ![]() -матрица для
фиксированного
-матрица для
фиксированного ![]() . Предположим также,
что
. Предположим также,
что ![]() ,
,
![]() – сильно выпуклые функции. Тогда задача (1) имеет единственное
решение.
– сильно выпуклые функции. Тогда задача (1) имеет единственное
решение.
Заметим, что
утверждение предложения 4 остается справедливым, если заменить индексное
множество ![]() на произвольное подмножество из
на произвольное подмножество из ![]() .
.
Для ограниченного случая предыдущий результат уточняется следующим образом.
Предложение
5 ([3],
теорема 4.8). Пусть ![]() дифференцируемое
дифференцируемое ![]() -отображение.
Предположим, что для каждого
-отображение.
Предположим, что для каждого ![]() ,
, ![]() есть
есть ![]() -матрица и
-матрица и ![]() есть
есть ![]() -матрица для
фиксированного
-матрица для
фиксированного ![]() . Предположим также,
что
. Предположим также,
что ![]() ,
,
![]() – сильно выпуклые функции и что
– сильно выпуклые функции и что ![]() – ограниченное
множество. Тогда задача (1) имеет единственное решение.
– ограниченное
множество. Тогда задача (1) имеет единственное решение.
Эти свойства позволяют получать результаты существования и единственности решений в модели экономического равновесия.
Модель экономического равновесия
Рассмотрим модель
экономического равновесия в условиях совершенной конкуренции, в которой
рассматривается рынок ![]() типов товаров. Предположим, что
каждый производитель производит единственный товар, но при этом отображение
предложения в общем случае многозначно. Это возможно, например, когда
существует несколько технологий процессов производства. Без ограничения
общности тогда можно считать, что каждый
типов товаров. Предположим, что
каждый производитель производит единственный товар, но при этом отображение
предложения в общем случае многозначно. Это возможно, например, когда
существует несколько технологий процессов производства. Без ограничения
общности тогда можно считать, что каждый ![]() -й производитель
производит единственный
-й производитель
производит единственный ![]() -й товар,
-й товар, ![]() . Тогда при данном
векторе цен
. Тогда при данном
векторе цен ![]() , отображение предложения представимо в виде
, отображение предложения представимо в виде
 , где
, где ![]() ,
, ![]() Если каждое отображение
Если каждое отображение
![]() монотонно, то
монотонно, то ![]() , где
, где ![]() – выпуклая функция
(см., например, [12]). Спрос
– выпуклая функция
(см., например, [12]). Спрос ![]() -го потребителя на
товары при данном векторе цен
-го потребителя на
товары при данном векторе цен ![]() определим следующим
образом:
определим следующим
образом:
![]() ,
,
где ![]() – вектор, задающий
запасы товаров
– вектор, задающий
запасы товаров ![]() -ого потребителя,
-ого потребителя, ![]() – функция спроса
– функция спроса ![]() -го потребителя,
которая имеет вид:
-го потребителя,
которая имеет вид: ![]() , где
, где ![]() ,
, ![]() ,
, 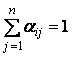 , т.е. она является
функцией типа Кобба-Дугласа.
, т.е. она является
функцией типа Кобба-Дугласа.
Обозначим через ![]() отображение
избыточного спроса, т.е.
отображение
избыточного спроса, т.е. ![]() , и положим
, и положим ![]() и
и ![]() . Заметим, что
модель не изменится, если в ней будут присутствовать потребители со спросом на
единственный товар каждый, тогда
. Заметим, что
модель не изменится, если в ней будут присутствовать потребители со спросом на
единственный товар каждый, тогда ![]() будет определяться
как отображение избыточного предложения на
будет определяться
как отображение избыточного предложения на ![]() -й товар без учета
общего спроса
-й товар без учета
общего спроса ![]() . Поэтому в дальнейшем присутствие
таких потребителей в модели явно оговариваться не будет, т.е. общий спрос
формируют
. Поэтому в дальнейшем присутствие
таких потребителей в модели явно оговариваться не будет, т.е. общий спрос
формируют ![]() потребителей.
потребителей.
Решая систему условий оптимальности для
задачи ![]() -го потребителя:
-го потребителя:
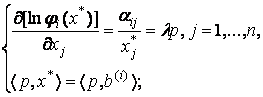
получим, что

Поэтому 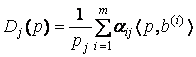 для
для ![]() . Итак, отображение спроса в данной модели
однозначно.
. Итак, отображение спроса в данной модели
однозначно.
Как известно, при
наличии только ограничений неотрицательности переменных, вектор ![]() называется вектором
равновесных цен, если он является решением следующей задачи дополнительности:
называется вектором
равновесных цен, если он является решением следующей задачи дополнительности:
![]()
см., например, [10], [13]. В данной работе будем предполагать, что допустимые цены содержатся в множестве, ограниченном параллелепипедом:
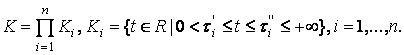
Другими словами,
цена каждого товара, вовлеченного в рынок, имеет нижнюю положительную границу и
может иметь верхнюю границу. Тогда задача нахождения равновесных цен может быть
сформулирована в виде смешанного вариационного неравенства: Найти точку ![]() такую, что
такую, что
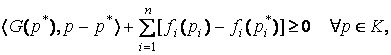 (2)
(2)
где
![]() см. [3].
см. [3].
Определение
5 (см.,
например, [13]). Отображение ![]()
a) обладает
свойством валовой заменимости, если ![]() ,
, ![]() ;
;
b) положительно однородно степени ![]() , если
, если ![]() для любого
для любого ![]() .
.
По построению,
отображение ![]() (или
(или ![]() ) положительно
однородно степени 0. Далее, мы видим, что
) положительно
однородно степени 0. Далее, мы видим, что ![]() где
где

Значит, ![]() есть
есть ![]() -матрица. Поэтому
отображение спроса
-матрица. Поэтому
отображение спроса ![]() удовлетворяет условию валовой
заменимости. Кроме того, имеем
удовлетворяет условию валовой
заменимости. Кроме того, имеем
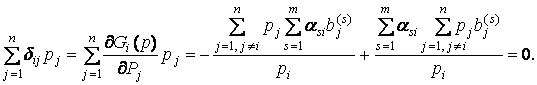 (3)
(3)
Из предложения 1 следует, что ![]() есть
есть ![]() -матрица для любого
элемента
-матрица для любого
элемента ![]() и, следовательно,
и, следовательно, ![]() есть
есть ![]() -отображение.
-отображение.
Уточним некоторые общие результаты существования и единственности решения для задачи (2).
Предложение
6. Пусть
![]() ограниченное множество. Тогда задача (2) имеет
решение. Если же отображения
ограниченное множество. Тогда задача (2) имеет
решение. Если же отображения ![]() строго монотонны
для
строго монотонны
для ![]() то задача (2) имеет
единственное решение.
то задача (2) имеет
единственное решение.
Доказательство следует из предложения 2 и следствия 1.
Предложение
7. Если отображения ![]() , строго монотонны,
то задача (2)
может иметь не более одного решения. Если же они сильно монотонны, то задача (2)
имеет единственное решение.
, строго монотонны,
то задача (2)
может иметь не более одного решения. Если же они сильно монотонны, то задача (2)
имеет единственное решение.
Доказательство следует из предложения 3a.
Кроме того,
используя полученные свойства отображения ![]() и предложения 5, 6,
получаем следующее утверждение.
и предложения 5, 6,
получаем следующее утверждение.
Предложение
8. Предположим, что для любого фиксированного ![]() функции
функции ![]() сильно выпуклые и
либо
сильно выпуклые и
либо
а) ![]() есть
есть ![]() -матрица для всех
-матрица для всех ![]() , где
, где ![]() ограниченное множество,
либо
ограниченное множество,
либо
b) ![]() такое, что
такое, что ![]() есть
есть ![]() -матрица для всех
-матрица для всех ![]() .
.
Тогда задача (2) имеет единственное решение.
Конкретизируем эти свойства для рассматриваемой задачи. Начнем с ограниченного случая.
Теорема
1. Предположим, что ![]() ограниченное
множество и существует индекс
ограниченное
множество и существует индекс ![]() такой, что
такой, что
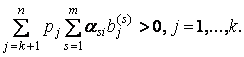
Пусть также отображения ![]() сильно монотонны.
Тогда задача (2)
имеет единственное решение.
сильно монотонны.
Тогда задача (2)
имеет единственное решение.
Доказательство.
Напомним,
что ![]() есть
есть ![]() -матрица. Из (3) и сделанных предположений следует, что
-матрица. Из (3) и сделанных предположений следует, что

![]() Согласно
предположению 1, это значит, что
Согласно
предположению 1, это значит, что ![]() есть
есть ![]() -матрица. Применяя
предложение 8a, получаем требуемый результат.
-матрица. Применяя
предложение 8a, получаем требуемый результат.
Приведем дополнительное достаточное условие для существования единственного решения для задачи (2).
Следствие 2. Пусть ![]() ограниченное
множество и
ограниченное
множество и
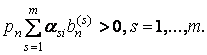 (4)
(4)
Пусть также отображения ![]() сильно монотонны.
Тогда задача (2)
имеет единственное решение.
сильно монотонны.
Тогда задача (2)
имеет единственное решение.
Доказательство следует из теоремы 1 при ![]()
Далее, поскольку все
отображения ![]() не сильно монотонны, мы можем заменить
основное отображение
не сильно монотонны, мы можем заменить
основное отображение ![]() в (2) на отображение
в (2) на отображение ![]() , элементы которого
определены следующим образом
, элементы которого
определены следующим образом
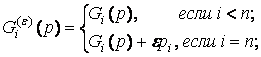
где ![]() произвольное
достаточно маленькое число. Если выполняется условие (4), то такое
"возмущенное" смешанное вариационное неравенство будет иметь
единственное решение, которое совпадает с решением исходной задачи.
произвольное
достаточно маленькое число. Если выполняется условие (4), то такое
"возмущенное" смешанное вариационное неравенство будет иметь
единственное решение, которое совпадает с решением исходной задачи.
Установим сходные результаты для неограниченного случая.
Теорема
2. Предположим, что существует ![]() и индекс
и индекс ![]() такой, что для
любого
такой, что для
любого ![]() выполняется
выполняется
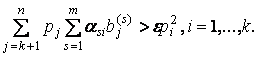
Если, дополнительно, ![]() сильно монотонны,
то задача (2)
имеет единственное решение.
сильно монотонны,
то задача (2)
имеет единственное решение.
Доказательство. Мы видим, что ![]() где
где

Напомним, что ![]() есть
есть ![]() -матрица. Из (3) и
предположений выше следует, что
-матрица. Из (3) и
предположений выше следует, что
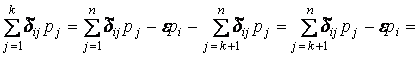
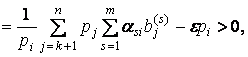
![]() .
.
Значит, ![]() есть
есть ![]() -матрица, и результат следует из предложения
8b.
-матрица, и результат следует из предложения
8b.
Приведем более простое условие, которое гарантирует единственное решение для задачи (2).
Следствие
3. Предположим, что существует ![]() такое, что для
любого
такое, что для
любого ![]() выполняется
выполняется
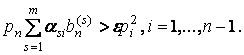
Предположим также, что ![]() сильно монотонно.
Тогда задача (2)
имеет единственное решение.
сильно монотонно.
Тогда задача (2)
имеет единственное решение.
Для доказательства
результата необходимо положить ![]() в теореме 2.
в теореме 2.
Снова, поскольку все
отображения ![]() не сильно монотонны, мы можем применить
регуляризацию. Заметим, что результаты теорем 1 и 2 остаются истинными, если мы
заменим подмножество
не сильно монотонны, мы можем применить
регуляризацию. Заметим, что результаты теорем 1 и 2 остаются истинными, если мы
заменим подмножество ![]() на произвольное подмножество из
на произвольное подмножество из ![]() . Также останутся
истинными результаты следствий 2 и 3, если заменить
. Также останутся
истинными результаты следствий 2 и 3, если заменить ![]() на произвольное
число из
на произвольное
число из ![]()
Таким образом, вместе с известными результатами существования и единственности решения для задачи экономического равновесия приведенный подход позволил нам получить некоторые новые результаты.
Решение
задачи равновесия с помощью ![]() -интервальных
функций
-интервальных
функций
Полученные свойства
позволяют найти решение задачи экономического равновесия, описанной в
предыдущем разделе, с помощью обычных методов дифференцируемой оптимизации на
основе аппарата ![]() -интервальных
функций. Определим функцию
-интервальных
функций. Определим функцию
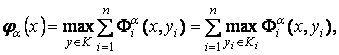 (5)
(5)
где ![]() для
для ![]() и
и ![]() . Функция
. Функция ![]() сильно вогнута,
значит существует единственное решение каждой подзадачи в (5), т.е. существует
элемент
сильно вогнута,
значит существует единственное решение каждой подзадачи в (5), т.е. существует
элемент ![]() такой, что
такой, что ![]() , для
, для ![]() . Положим
. Положим ![]() . Ясно, что точка
. Ясно, что точка ![]() является решением
задачи
является решением
задачи
![]()
для любого фиксированного ![]() . Как известно (см.,
например, [9]) функция
. Как известно (см.,
например, [9]) функция ![]() является интервальной
для задачи (2), т.е. вместо нее можно решать задачу минимизации функции
является интервальной
для задачи (2), т.е. вместо нее можно решать задачу минимизации функции ![]() на
на ![]() :
:
![]() .
.
Решение этой задачи может вызвать
дополнительные трудности из-за недифференцируемости функции ![]() . В работе [4] был
предложен иной подход, связанный с использованием
. В работе [4] был
предложен иной подход, связанный с использованием ![]() -интервальных
функций. Следуя [4], определим функцию
-интервальных
функций. Следуя [4], определим функцию ![]() , где
, где ![]() . Свойства функции
. Свойства функции ![]() называемой также
называемой также ![]() -интервальной,
формулируются следующим образом.
-интервальной,
формулируются следующим образом.
Предложение 9 ([4], предложение 8, теоремы 1 и 2).
a)
![]() для всех
для всех ![]()
b) ![]() тогда и только
тогда, когда
тогда и только
тогда, когда ![]() – решение задачи (2).
– решение задачи (2).
c) Функция ![]() непрерывно
дифференцируемая и
непрерывно
дифференцируемая и
![]()
d) Пусть ![]() есть
есть ![]() -матрица для всех
-матрица для всех ![]() . Если
. Если
![]() ,
(6)
,
(6)
то
![]() и
и ![]() решение задачи (2).
решение задачи (2).
Иначе говоря, если
якобиан основного отображения ![]() есть
есть ![]() -матрица, то
смешанное вариационное неравенство (2) эквивалентно задаче нахождения
стационарной точки непрерывно дифференцируемой функции, т.е. решению системы
нелинейных уравнений (6). Задача решения системы (6) может быть решена
стандартными методами дифференцируемой оптимизации без ограничений, например
такими, как градиентный метод или метод сопряженных градиентов. Для проверки
эффективности предложенного подхода и проведения численных расчетов были
выбраны следующие реализации этих методов применительно к решению задачи (6).
-матрица, то
смешанное вариационное неравенство (2) эквивалентно задаче нахождения
стационарной точки непрерывно дифференцируемой функции, т.е. решению системы
нелинейных уравнений (6). Задача решения системы (6) может быть решена
стандартными методами дифференцируемой оптимизации без ограничений, например
такими, как градиентный метод или метод сопряженных градиентов. Для проверки
эффективности предложенного подхода и проведения численных расчетов были
выбраны следующие реализации этих методов применительно к решению задачи (6).
Алгоритм 1. Градиентный метод (ГМ) (см., например, [14]).
Выберем начальную
точку ![]() , числа
, числа ![]() На
На ![]() -й итерации,
-й итерации, ![]() имеем точку
имеем точку ![]() .
.
Шаг 1. Полагаем ![]()
Шаг 2. Вычисляем наименьшее неотрицательное
целое ![]() такое, что
такое, что
![]()
Шаг 3. Полагаем ![]() и переходим к следующей итерации.
и переходим к следующей итерации.
Алгоритм 2. Метод сопряженных градиентов (МСГ) из [15].
Выберем начальную
точку ![]() и числа
и числа ![]()
![]() Полагаем
Полагаем ![]() ,
, ![]() . На
. На ![]() -ой итерации,
-ой итерации, ![]() имеем точку
имеем точку ![]() .
.
Шаг 1. Если ![]() алгоритм завершает
работу.
алгоритм завершает
работу.
Шаг 2. Полагаем

и выбираем ![]()
Шаг 3. Определяем
число ![]() такое, что точка
такое, что точка ![]() и вектор
и вектор
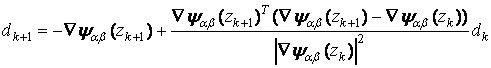
удовлетворяют условиям:
![]()
![]()
Полагаем
![]() и переходим к следующей итерации.
и переходим к следующей итерации.
При проведении
численных экспериментов для алгоритма 1 были взяты значения параметров: ![]() а для алгоритма 2
а для алгоритма 2 ![]() Параметры функции
Параметры функции ![]() были заданы
следующим образом:
были заданы
следующим образом: ![]() Функции
Функции ![]() определены в
соответствии с формулой:
определены в
соответствии с формулой:
![]()
где ![]() для всех
для всех ![]() Запасы товаров определяются
с помощью генератора случайных чисел в интервале (0, 10). Количество
потребителей
Запасы товаров определяются
с помощью генератора случайных чисел в интервале (0, 10). Количество
потребителей ![]() . Коэффициенты функции Кобба-Дугласа
были выбраны следующим образом:
. Коэффициенты функции Кобба-Дугласа
были выбраны следующим образом: ![]() ,
, ![]() . Была выбрана
стартовая точка
. Была выбрана
стартовая точка ![]() Использовался следующий критерий
останова:
Использовался следующий критерий
останова: ![]() Было проведено две серии экспериментов с
заданной точностью. В первой серии точность решения
Было проведено две серии экспериментов с
заданной точностью. В первой серии точность решения ![]() во второй серии
во второй серии ![]() Результаты
приведены в табл. 1 и 2. В таблицах It обозначает
количество итераций, t – время (сек.).
Результаты
приведены в табл. 1 и 2. В таблицах It обозначает
количество итераций, t – время (сек.).
Табл. 1.
|
ГМ |
МСГ |
Размерность |
||
|
It |
t |
It |
t |
n |
|
28 |
0.10 |
18 |
0.00 |
3 |
|
30 |
0.10 |
20 |
0.00 |
5 |
|
33 |
0.10 |
22 |
0.10 |
10 |
|
34 |
0.21 |
23 |
0.10 |
15 |
|
35 |
0.32 |
23 |
0.10 |
20 |
|
35 |
0.38 |
23 |
0.16 |
25 |
|
36 |
0.49 |
23 |
0.21 |
30 |
|
37 |
0.93 |
24 |
0.38 |
50 |
На основании
проведенных расчетов можно заключить, что оба алгоритма сходятся достаточно
быстро, но с увеличением размерности преимущество метода сопряженных градиентов
возрастает. Таким образом, этот метод, примененный к минимизации ![]() -интервальной
функции, является достаточно эффективным инструментом для решения смешанных вариационных
неравенств, следовательно, и задачи экономического равновесия с функцией спроса
типа Кобба-Дугласа.
-интервальной
функции, является достаточно эффективным инструментом для решения смешанных вариационных
неравенств, следовательно, и задачи экономического равновесия с функцией спроса
типа Кобба-Дугласа.
Табл. 2.
|
ГМ |
МСГ |
Размерность |
||
|
It |
t |
It |
t |
n |
|
71 |
0.10 |
46 |
0.00 |
3 |
|
74 |
0.16 |
48 |
0.10 |
5 |
|
77 |
0.32 |
50 |
0.10 |
10 |
|
78 |
0.49 |
51 |
0.16 |
15 |
|
78 |
0.65 |
51 |
0.21 |
20 |
|
78 |
0.87 |
51 |
0.27 |
25 |
|
79 |
1.15 |
51 |
0.38 |
30 |
|
80 |
2.30 |
52 |
0.87 |
50 |