О ПРОГНОЗИРОВАНИИ СПРОСА НА ТОВАРЫ
Источник: http://ipian.kazan.ru/science/sbornik6.html
Введение
Одной из важнейших функций управления предприятиями является прогнозирование спроса на товары. Эффективное прогнозирование спроса на основе имеющихся реальных статистических данных является во многом определяющим фактором в жесткой конкурентной борьбе. Прогнозирование спроса является ядром систем управления запасами и определяет в значительной мере их эффективность.
Подавляющее большинство работ в области прогнозирования спроса сводится к перечислению разнообразных факторов, влияющих на спрос, и к качественному анализу влияния этих факторов. Однако для создания эффективных систем прогнозирования спроса необходимы методы обработки статистических данных, обеспечивающие качественные прогнозы спроса. А для этого, прежде всего, необходимо разработать математическую модель динамики спроса. С одной стороны эта модель должна учитывать все основные факторы, влияющие на спрос. С другой стороны, количество этих факторов следует выбирать по возможности не очень большим, так как с увеличением количества оцениваемых факторов увеличивается количество оцениваемых по статистическим данным коэффициентов модели, что приводит к снижению эффективности их оценок. Кроме того, математическая модель динамики спроса должна базироваться на статистических данных, реально имеющихся на предприятии. Моделированию динамики спроса для его прогнозирования посвящена работа [1], в которой приводится перечень факторов, влияющих, по мнению авторов, на спрос, и определяются методы измерения некоторых из этих факторов. Настоящая статья является развитием работы [1] для прогнозирования спроса на товары при розничной торговле. Для этой сферы деятельности предлагается отчасти иной набор факторов, учитываемых при моделировании спроса, формируются методы измерения для всех рассматриваемых факторов. В отличие от работы [1] подробно описываются и обосновываются методы прогнозирования спроса, а также алгоритмы предварительной подготовки статистических данных и идентификации модели.
Математическая модель динамики спроса
Пусть Y(i) – спрос на некоторый товар в момент времени i. Под моментом времени понимается некоторый интервал, принимаемый за единицу измерения времени. За единицу измерения времени предлагается выбрать неделю. Выбор в качестве единицы измерения времени интервала большей длины приведет к уменьшению количества статистических данных. Выбор в качестве единицы измерения времени суток потребует учета в модели колебаний спроса в зависимости от дня недели. А для этого потребуется ввести в модель m-1 дополнительных членов, где m – количество рабочих дней стандартной недели на данном предприятии (m может быть равно 5, 6 или 7), и оценивать по статистическим данным коэффициенты при этих членах. В силу старения информации даже при значительном количестве статистических данных на оценки коэффициентов модели должно оказывать существенное влияние не очень большое количество последних данных. Поэтому увеличение числа оцениваемых коэффициентов на m-1 приведет к уменьшению среднего количества статистических данных на оценку одного коэффициента, и, следовательно, к уменьшению точности оценок коэффициентов. А это может повлечь ухудшение качества прогнозов. Прогнозировать спрос может потребоваться на интервалы времени с точностью до суток. При этом следует учитывать колебания спроса в зависимости от дня стандартной недели. Под стандартной понимается рабочая неделя, в которой отсутствуют праздничные дни. Для учета колебаний спроса в зависимости от дня стандартной недели предлагается оценивать по статистическим данным веса каждого рабочего дня стандартной недели.
Фактически данные о спросе на товары имеются за сутки.
При этом возможны пропуски статистических данных из-за праздничных дней и отсутствия
рассматриваемого товара в некоторые рабочие дни. Поэтому перед моделированием
динамики спроса необходимо провести предварительную подготовку данных. Ее целью
является оценивание весов рабочих дней стандартной недели и определение спроса
за каждую неделю. Пусть dj(i) – вес j-го
рабочего дня стандартной недели при ![]() за первые i недель.
Тогда эти веса предлагается оценивать по рекуррентной формуле
за первые i недель.
Тогда эти веса предлагается оценивать по рекуррентной формуле
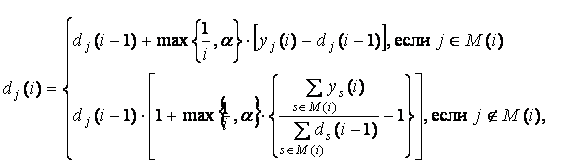 (1)
(1)
где
yj(i) – спрос на рассматриваемый товар в j-й
рабочий день i–й недели; M(i)
– множество рабочих дней i–й недели, в
которые можно было реализовать этот товар, а α – параметр настройки из
интервала [0;0,1]. Параметр α вводится для учета старения информации и
принимает тем большее значение, чем в большей степени стареет информация.
Значение α определяется при идентификации модели. Для объяснения этой
формулы заметим, что, если старение информации не учитывать, т.е. α=0, и
статистические данные имеются за все дни, т.е. ![]() для всех
для всех ![]() , то данная формула будет представлять
собой рекуррентную форму вычисления среднего арифметического спроса за j-е дни недели. А если в i-ю неделю величина
, то данная формула будет представлять
собой рекуррентную форму вычисления среднего арифметического спроса за j-е дни недели. А если в i-ю неделю величина ![]() отсутствует, то ее предлагается
восстанавливать по формуле
отсутствует, то ее предлагается
восстанавливать по формуле
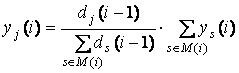 .
.
В соответствии с этим подходом спрос за i-ю неделю предлагается определять по формуле

Для любого будущего момента времени значение спроса
неизвестно. Поэтому последовательность величин ![]() при различных i
представляет собой временной ряд [2, 3], или в иной терминологии – случайный процесс
с дискретным временем. Нашей задачей в этом разделе является построение
математической модели этого временного ряда. Структура этой модели в какой-то
степени зависит от специфики товара и от цели моделирования. В данной статье
рассматривается спрос на продукты питания и алкоголь, а модель строится для
прогнозирования спроса на эти товары в процессе управления их оптовой
торговлей. Предлагаемая модель или ее отдельные компоненты могут быть
использованы для моделирования спроса на товары и иной природы. В результате
содержательного анализа экономической природы спроса на рассматриваемые товары
и реальных статистических данных по этому спросу было признано целесообразным
при моделировании спроса на эти товары учитывать следующие факторы: закономерное
изменение спроса во времени; старение информации; сезонные колебания спроса в
течение года; предпраздничное увеличение спроса; зависимость спроса от цены
товара. Рассмотрим способы измерения каждого из перечисленных факторов.
при различных i
представляет собой временной ряд [2, 3], или в иной терминологии – случайный процесс
с дискретным временем. Нашей задачей в этом разделе является построение
математической модели этого временного ряда. Структура этой модели в какой-то
степени зависит от специфики товара и от цели моделирования. В данной статье
рассматривается спрос на продукты питания и алкоголь, а модель строится для
прогнозирования спроса на эти товары в процессе управления их оптовой
торговлей. Предлагаемая модель или ее отдельные компоненты могут быть
использованы для моделирования спроса на товары и иной природы. В результате
содержательного анализа экономической природы спроса на рассматриваемые товары
и реальных статистических данных по этому спросу было признано целесообразным
при моделировании спроса на эти товары учитывать следующие факторы: закономерное
изменение спроса во времени; старение информации; сезонные колебания спроса в
течение года; предпраздничное увеличение спроса; зависимость спроса от цены
товара. Рассмотрим способы измерения каждого из перечисленных факторов.
Закономерное изменение спроса во времени, и старение информации будем
моделировать совместно. Для большинства товаров спрос имеет тенденцию на
некоторых участках времени возрастать или убывать. Причем на некотором участке
он может возрастать, а затем убывать, или наоборот. Для моделирования этого
явления предлагается ввести в модель член ![]() , который определяется выражениями
, который определяется выражениями
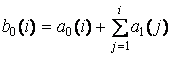 (2)
(2)
и
![]() при
при ![]() и 1,
(3)
и 1,
(3)
где ![]() и
и ![]() - последовательности некоррелированных
случайных величин, некоррелированных друг с другом, имеющих нулевые математические
ожидания и конечные не зависящие от времени дисперсии, т.е.
- последовательности некоррелированных
случайных величин, некоррелированных друг с другом, имеющих нулевые математические
ожидания и конечные не зависящие от времени дисперсии, т.е.
![]() при
при ![]() и 1, (4)
и 1, (4)
при при
 (5)
(5)
и
![]() (6)
(6)
Выражения (2) - (6) обобщают с учетом старения
информации обычную линейную функцию времени. С помощью случайных
последовательностей ![]() и
и
![]() моделируются
спонтанные изменения коэффициентов
моделируются
спонтанные изменения коэффициентов ![]() и
и ![]() временной части тренда
временной части тренда ![]() , и этим самым учитывается
старение информации. Скорость старения информации определяется параметрами
, и этим самым учитывается
старение информации. Скорость старения информации определяется параметрами ![]() и
и ![]() . Чем она больше, тем больше
должны быть значения параметров
. Чем она больше, тем больше
должны быть значения параметров ![]() и
и ![]() . Если старение информации отсутствует, то
. Если старение информации отсутствует, то ![]() =
=![]() =0, выражение (3) принимает вид
=0, выражение (3) принимает вид ![]() при k=0,1, а из выражения (2) следует, что
при k=0,1, а из выражения (2) следует, что ![]() . Для некоторых товаров
спрос может не иметь объективной тенденции ни возрастать, ни убывать ни на каких
участках временной оси. Для этих товаров временную часть тренда предлагается
определять выражением
. Для некоторых товаров
спрос может не иметь объективной тенденции ни возрастать, ни убывать ни на каких
участках временной оси. Для этих товаров временную часть тренда предлагается
определять выражением
![]() (7)
(7)
где ![]() удовлетворяет соотношениям (3) – (6).
Выражение (7) обобщает обычную константу
удовлетворяет соотношениям (3) – (6).
Выражение (7) обобщает обычную константу ![]() , в которую оно превращается, если
отсутствует старение информации и
, в которую оно превращается, если
отсутствует старение информации и ![]() =0. Предлагаемый способ учета закономерного
изменения спроса во времени и старения информации был впервые изложен в работе
[1]. Для моделирования всех, не учитываемых в явном виде факторов, предлагается
ввести в модель случайную составляющую
=0. Предлагаемый способ учета закономерного
изменения спроса во времени и старения информации был впервые изложен в работе
[1]. Для моделирования всех, не учитываемых в явном виде факторов, предлагается
ввести в модель случайную составляющую ![]() , удовлетворяющую соотношениям
, удовлетворяющую соотношениям
![]() (8)
(8)
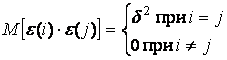 (9)
(9)
и
![]() при k=0,1. (10)
при k=0,1. (10)
Таким образом, стохастическая составляющая модели спроса будет определяться выражением
![]() (11)
(11)
где ![]() - определяется выражениями (2) – (6) или
выражениями (7) и (3) – (5). Согласно терминологии работы [3], случайный
процесс
- определяется выражениями (2) – (6) или
выражениями (7) и (3) – (5). Согласно терминологии работы [3], случайный
процесс ![]() ,
определяемый выражениями (2) – (6) и (8) – (11), называется процессом с наклонным
стохастическим трендом. Этим наклонным стохастическим трендом является величина
,
определяемый выражениями (2) – (6) и (8) – (11), называется процессом с наклонным
стохастическим трендом. Этим наклонным стохастическим трендом является величина
![]() . А если
. А если ![]() определяется
выражениями (3) – (5) и (7) – (11), то он называется процессом с горизонтальным
стохастическим трендом, роль которого играет величина
определяется
выражениями (3) – (5) и (7) – (11), то он называется процессом с горизонтальным
стохастическим трендом, роль которого играет величина ![]() .
.
Из оставшихся трех факторов наиболее заметное влияние на спрос, как правило, оказывают его сезонные колебания. В результате анализа фактических данных и в соответствии с принципом минимизации количества коэффициентов модели целесообразно использовать в течение года три периода: зиму, лето и межсезонье, включающее весну и осень. Для моделирования сезонных колебаний спроса предлагается использовать непрерывную кусочно-линейную функцию, аргументом которой является порядковый номер недели внутри года. Пики этой ломаной линии должны приходиться на середины зимы, весны, лета и осени. При этом высоты этих пиков в серединах весны и осени считаются одинаковыми. Все высоты пиков являются коэффициентами модели и должны оцениваться по статистическим данным. За середины зимы, весны, лета и осени принимаются, соответственно, 3-я, 15-я, 29-я и 42-я недели года. Тогда функция, моделирующая сезонные колебания спроса, будет иметь вид
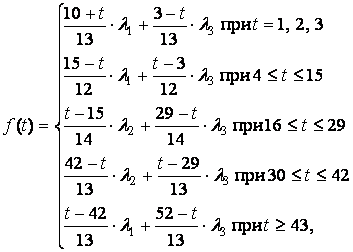 (12)
(12)
где ![]() - значение этой функции в середине зимы,
- значение этой функции в середине зимы, ![]() - значение данной
функции в середине лета и
- значение данной
функции в середине лета и ![]() - значение этой функции в середине весны и
в середине осени. Введем три базисные функции времени
- значение этой функции в середине весны и
в середине осени. Введем три базисные функции времени
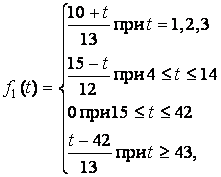 (13)
(13)
 (14)
(14)
и
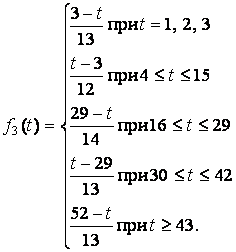 (15)
(15)
Из выражений (12) – (15) следует, что
![]() (16)
(16)
С другой стороны, из (13) – (15) имеем, что
![]()
Но тогда выражение (16) можно записать в виде
![]()
Свободный член ![]() отдельно в модели учитывать не следует,
так как он учтется вместе с членами
отдельно в модели учитывать не следует,
так как он учтется вместе с членами ![]() . Таким образом, для моделирования сезонных
колебаний спроса надо ввести в модель две базисные функции времени
. Таким образом, для моделирования сезонных
колебаний спроса надо ввести в модель две базисные функции времени ![]() и
и ![]() , определяемые выражениями (13) и
(14). Коэффициенты при этих базисных функциях будем обозначать
, определяемые выражениями (13) и
(14). Коэффициенты при этих базисных функциях будем обозначать ![]() и
и ![]() , где
, где ![]() при
при ![]() .
.
Для моделирования увеличения спроса в предпраздничные
дни предлагается использовать базисную функцию времени ![]() , определяемую следующей таблицей
, определяемую следующей таблицей
|
t |
8 |
9 |
10 |
16 |
17 |
24 |
25 |
33 |
34 |
35 |
43 |
44 |
49 |
50 |
51 |
t³52 |
|
f3(t) |
0,12 |
0,5 |
0,38 |
0,33 |
0,67 |
0,33 |
0,67 |
0,12 |
0,5 |
0,38 |
0,21 |
0,71 |
0,1×q |
0,2×q |
0,3×q |
0,4×q |
Для остальных значений t функция ![]() Интервалы увеличения
спроса в предпраздничные недели определялись экспертным путем. Веса этих недель
для каждого такого интервала определялись тоже экспертным путем. Вес увеличения
спроса перед Международным женским днем (8-е марта), майскими праздниками (1-е,
2-е и 9-е мая), сабантуем и Днем независимости Республики Татарстан принималось
за 1. Последние два праздника для Республики Татарстан. Поэтому для других
регионов России необходимо положить
Интервалы увеличения
спроса в предпраздничные недели определялись экспертным путем. Веса этих недель
для каждого такого интервала определялись тоже экспертным путем. Вес увеличения
спроса перед Международным женским днем (8-е марта), майскими праздниками (1-е,
2-е и 9-е мая), сабантуем и Днем независимости Республики Татарстан принималось
за 1. Последние два праздника для Республики Татарстан. Поэтому для других
регионов России необходимо положить ![]() при
при ![]() 24, 25, 33, 34, 35. Для праздника Дня
согласия и примирения в результате экспертного анализа вес увеличения спроса
принимался за 0,92. А увеличение спроса в предновогодние недели считается
равным параметру настройки θ. Значение этого параметра настройки
должно определяться при идентификации модели.
24, 25, 33, 34, 35. Для праздника Дня
согласия и примирения в результате экспертного анализа вес увеличения спроса
принимался за 0,92. А увеличение спроса в предновогодние недели считается
равным параметру настройки θ. Значение этого параметра настройки
должно определяться при идентификации модели.
При моделировании зависимости спроса от цены следует учитывать
запаздывание во времени и тот факт, что для некоторых потребителей спрос
зависит не от самой цены, а от ее изменения. Поэтому для моделирования
зависимости спроса от цены предлагается использовать базисную функцию ![]() , определяемую
выражением
, определяемую
выражением
![]() (17)
(17)
где ![]() - цена данного товара в i-ю
неделю, τ – параметр настройки, характеризующий запаздывание
влияния цены на спрос, γ – параметр настройки из интервала [0;1], а
- цена данного товара в i-ю
неделю, τ – параметр настройки, характеризующий запаздывание
влияния цены на спрос, γ – параметр настройки из интервала [0;1], а
![]() - изменение
цены рассматриваемого товара за i-ю неделю, определяемое
формулой
- изменение
цены рассматриваемого товара за i-ю неделю, определяемое
формулой
![]() (18)
(18)
Параметр настройки γ характеризует долю
потребителей, реагирующих на абсолютную величину цены. Параметры настройки τ
и γ должны определяться при идентификации модели. Из выражений (17)
и (18) следует, что базисная функция ![]() определяется формулой
определяется формулой
![]() (19)
(19)
Таким образом, математическая модель динамики спроса на рассматриваемый товар определяется выражением
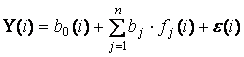 ,
(20)
,
(20)
где ![]() - временная часть тренда спроса,
учитывающая его закономерное изменение во времени и старение информации,
- временная часть тренда спроса,
учитывающая его закономерное изменение во времени и старение информации, ![]() - количество базисных
функций времени в модели,
- количество базисных
функций времени в модели, ![]() - j-я базисная
функция времени,
- j-я базисная
функция времени, ![]() -
оцениваемые по статистическим данным коэффициенты модели при
-
оцениваемые по статистическим данным коэффициенты модели при ![]() , а
, а ![]() - модельная ошибка,
удовлетворяющая условиям (8) – (10). Количество базисных функций
- модельная ошибка,
удовлетворяющая условиям (8) – (10). Количество базисных функций ![]() не превышает 4. При
этом базисные функции
не превышает 4. При
этом базисные функции ![]() и
и
![]() могут
присутствовать или отсутствовать в модели только вместе. Базисные функции
могут
присутствовать или отсутствовать в модели только вместе. Базисные функции ![]() ,
, ![]() и
и ![]() определяются, соответственно, выражениями
(13), (14) и (19), а базисная функция
определяются, соответственно, выражениями
(13), (14) и (19), а базисная функция ![]() задается таблицей. Временная часть тренда
задается таблицей. Временная часть тренда ![]() определяется
выражениями (2) – (6) или (3) – (7).
определяется
выражениями (2) – (6) или (3) – (7).