По мере развития машиностроения, прежде всего, автоматизировались наиболее сложные и трудоемкие операции, связанные с изменениями формы и размеров изделий. Загрузка и разгрузка технологического оборудования осуществлялась обычно вручную или простейшими средствами механизации. В последнее время в связи с задачами комплексной автоматизации производства и освоения новых областей деятельности человека большое внимание уделяется автоматизации операций манипулирования - перемещения и ориентации изделий и инструмента.
Современное автоматизированное сборочное оборудование (АСО) представляет собой комплекс сложных динамических систем. Сложность их обусловлена высокими требованиями к производительности и точности работы сборочного оборудования, а также разнообразием выполняемых им функций. Одним из важнейших вопросов, которые необходимо решать при проектировании и эксплуатации таких следящих систем, является вопрос об устойчивости системы. Другой не менее важный вопрос разработки - это обеспечения бесскачкообразного режима работы системы и плавности переходных процессов в системе управления.
Возникновение скачков на исполнительной оси отрицательно сказывается на качестве работы и динамической точности следящей системы АСО. Осуществление плавного режима работы следящих систем АСО возможно либо изменением конструктивных параметров системы, либо вводом в эту систему корректирующих устройств. Последний путь более предпочтителен.
В данной работе рассмотрены инженерные методы синтеза, дающие возможность определить в проектируемой следящей системе АСО наличие плавного режима работы во всем рабочем диапазоне скоростей, и, в случае его отсутствия, необходимые виды корректирующих устройств. С помощью корректирующих устройств в следящей системе одновременно добиваются больших запасов устойчивости системы, безскачкообразного режима работы исполнительной оси в рабочем диапазоне скоростей и плавности переходных процессов в системе управления. Использование конкретного вида корректирующих устройств определяется как возможностью эффективного увеличения диапазона плавных скоростей, так и условиями осуществления коррекции в конкретных следящих системах АСО.
В задачу регулирования движения манипулятора входят построение динамической модели манипулятора и выбор на основе этой модели законов управления, обеспечивающих заданное поведение системы.
При синтезе систем управления современных промышленных роботов принято рассматривать приводы сочленений манипулятора как сервомеханизмы. Такой подход неадекватно отражает переменные динамические характеристики манипулятора, поскольку не учитывает движения и конфигурации манипулятора в целом.
В ряде случаев нестабильность параметров управляемой системы делает традиционные методы управления с обратной связью практически не эффективными. При этом возрастает инерционность и колебательность процессов обработки заданных команд, что приводит к снижению точности и скорости движения рабочего органа и ограничивает область применения манипуляторов работами, не требующими высокой точности. Движение манипуляторов, управляемых указанным образом, характеризуется низкой скоростью и вредными вибрациями. Сколько-нибудь значительное улучшение качества функционирования манипулятора может быть достигнуто лишь на основе использования более точных динамических моделей, синтеза достаточно точных законов управления и применения специализированных компьютеров с параллельной обработкой данных.
В этой работе рассматриваются вопросы синтеза законов управления, дающих возможность на базе построенных динамических моделей осуществлять эффективное управление манипулятором. Этого позволяет добиться использование в качестве математического аппарата управления современных методов теории управления, а именно метода пространства состояний и теории модального управления. Применение методов пространства состояний для дискретных динамических систем к математическому описанию манипулятора является более предпочтительным в сравнении с методами для непрерывных систем, поскольку реальное управление любым манипулятором осуществляется цифровой ЭВМ дискретным способом. В связи с этим, рассмотрение динамики манипулятора в дискретном времени позволяет избежать ошибок связанных с квантованием сигналов в аналого-цифровых преобразователях, включаемых в систему управления.

Управление движением манипуляционных роботов
Если движения роботов достаточно скоротечные, быстрые, то сочленениями робота нельзя управлять независимо, поскольку динамическое взаимодействие между звеньями становится чрезвычайно большим и требуется нелинейный или комбинированный алгоритм управления. В общем случае для построения алгоритмов нелинейного управления робот разбивается на две подсистеме (минимальную и терминальную). Динамические переменные (углы, скорости, ускорения и моменты) конфигурации и далее для любого задания прилагаются компенсирующие управляющие моменты во время движения. Таким образом, задача управления заключается в том, чтобы найти необходимые моменты, которые желаемым образом управляют сочленением в каждый момент времени[2]. Очевидно, что в силу эффектов взаимного влияния инерционных, кориолисовых, центробежных и гравитационных нагрузок, которые непрерывно изменяются, чрезвычайно трудно, если вообще возможно, добиться настоящего управления в реальном времени.
В данной работе для упрощения математической модели манипулятора положим, что робот движется на невысоких скоростях. В этом случае на систему не действуют какие-либо значительные взаимовлияющие динамические силы. Простым решением управления при этом является независимое управление каждым сочленением. Это так называемый принцип пропорционального управления, который может быть применим для большинства приложений.
Устройство управления манипулятором рассмотрим на примере робота Puma серии 560[1]. Устройство управления состоит из вычислительного устройства ВУ и шести микропроцессорных устройств МП, каждый из которых имеет цифро-аналоговый преобразователь ЦАП и кодирующее устройство КУ.
ВУ выполняет две функции: 1) взаимодействие с пользователем; 2) координацию работы микропроцессоров. Основной из задач возлагаемых на ВУ является планирование траектории движения с учетом интерполяции в сочленениях, включающее приращение параметров, соответствующее каждому моменту времени с дискретностью Т1 и каждому сочленению, а также передача информации о завершении движения по всем осям в микропроцессоры, где формируются управляющие воздействия в соответствии с требованиями движения по приращениям.
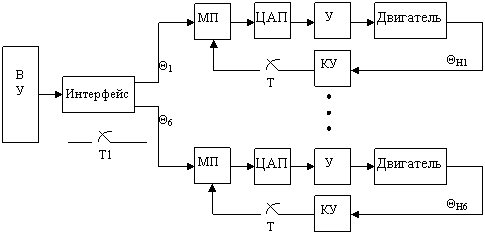
Рисунок 1 - Схема управления манипулятором
На нижнем уровне для управления каждым сочленением имеется свой контур управления, который оперирует информацией об ошибке позиционирования и обменивается данными с микропроцессором через интервалы времени Т, причем период дискретности Т должен быть намного меньше Т1.
Основными функциями микропроцессора являются:
1. получение и обработка опорных точек траектории от ВУ и проведение интерполяции между текущими и заданными значениями параметров сочленения через интервалы времени Т1;
2. считывание значений величин приращений от кодирующего устройства через время Т;
3. накопление и преобразование сигналов ошибки в электрический кодовый сигнал, который организует движение в сочленениях.
В данной работе ставится задача синтеза такого регулятора, который, будучи включенным в подсистему на нижнем уровне, путем программного определения необходимых параметров управления, обрабатываемых микропроцессором, обеспечивал бы управление движением манипулятора с необходимым качеством.

Математическая модель привода манипулятора в виде передаточной функции
При анализе одного сочленения манипулятора сначала будем рассматривать как непрерывную линейную систему, к которой может быть применен аппарат преобразования Лапласа.
Большинство промышленных роботов с электрическим приводом чаще всего оснащаются двигателями постоянного тока с независимым возбуждением в каждом сочленении. Двигатели постоянного тока сочетают в себе такие качества, как высокая мощность, плавность хода, возможность работы на малых скоростях, линейность нагрузочной характеристики и небольшие постоянные времени.
Использование постоянного магнитного поля и энергии постоянного тока обеспечивает максимальный момент при минимальной энергии, затрачиваемой на питание, и при минимальном весе. Эти параметры также позволяют снизить индуктивность двигателя и, следовательно, величину электромагнитной постоянной времени двигателя, обусловленную электрическими взаимодействиями. На рисунке 2 приведена эквивалентная схема нагруженного двигателя постоянного тока с управлением в цепи якоря, который может быть использован в сочленении манипулятора.
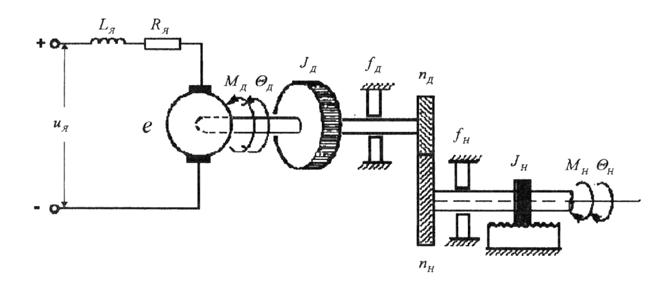
Рисунок 2 - Эквивалентная схема нагруженного двигателя постоянного тока с якорным управлением
Основными переменными в данной схеме являются:
uя – напряжение, приложенное к якорной обмотке двигателя, В;
iя – ток в цепи якоря, А;
Lя – индуктивность якорной цепи, Гн;
Rя – сопротивление якорной цепи, Ом;
е – напряжение противо-эдс, В;
Mд – момент двигателя, отнесенный к валу двигателя, Н*м/рад;
Θд – угловое перемещение вала двигателя, рад.;
Θн – угловое перемещение вала нагрузки, рад.;
Jд – момент инерции двигателя приведенный к валу двигателя, Н*м*с2/рад;
Jн – момент инерции нагрузки приведенный к валу нагрузки, Н*м*с2/рад;
fд – коэффициент вязкого трения в подшипниках двигателя приведенный к валу двигателя, Н*м*с/рад;
fн – коэффициент вязкого трения в подшипниках нагрузки приведенный к валу нагрузки, Н*м*с/рад;
nд – число зубьев шестерни редуктора на валу двигателя;
nн – число зубьев шестерни редуктора на валу нагрузки.
Текущее угловое перемещение сочленения может быть измерено с помощью фотоэлектрического первичного преобразователя с перекрытием света - оптического кодирующего устройства, включенного по схеме накапливающего типа [3]. В этом случае подаваемые на входы микропроцессора сравниваемые напряжения являются пропорциональными желаемому и действительному углам поворота сочленения манипулятора, и задаются в цифровом виде.
Таким образом, для следящих систем роботов манипуляторов с микропроцессорным управлением углы поворота задаются эквивалентными напряжениями. Соответствующая структурная схема следящей системы одного сочленения робота манипулятора представлена на рис. 3.
Передаточную функцию для разомкнутой системы, связывающую подаваемое на вход усилителя мощности напряжение рассогласования uум(f) и напряжение от датчика положения uн(t),пропорциональное углу поворота вала сочленения, можно записать выражением:
 (1)
(1)
где Кр - коэффициент передачи измерителя рассогласования, включающий коэффициент передачи датчика угла поворота выходного вала, приведенного к валу двигателя.
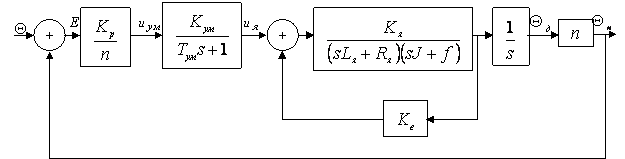
Рисунок 3 – Следящая система шарнира робота манипулятора

Описание дискретной следящей системы шарнира манипулятора в пространстве параметров состояний
В дискретном времени рекуррентное векторно-матричное уравнение данного объекта и уравнение выхода имеют вид:
 (2)
(2)
где x(k) - вектор состояния,
u(k) - вектор управления,
Ф(T) - матрица перехода состояния дискретной системы,
Н(Т) - вектор управляемого перехода дискретной системы,
Т - период дискретизации, равный интервалу времени, через который микропроцессор на нижнем уровне системы управления считывает данные о текущем угле поворота от датчика.

Синтез модального регулятора
Задача аналитического конструирования регулятора для дискретного объекта управления заключается в выборе структуры и параметров регулятора, вырабатывающего по информации поступающей с измерителя состояния, управление u(k), обеспечивающее проектируемой системе требуемую совокупность показателей качества.
Под совокупностью показателей качества будем понимать набор величин, определяющих качество переходных процессов в системе, таких как: время переходного процесса tп, перерегулирование δ, а также другие.
Поскольку, текущее значение вектора состояния x(k) объекта управления, дает полную информацию об объекте управления и внешних воздействиях в данный момент времени и включает в себя предысторию о поведении в прошлом, поэтому закон управления, вырабатываемый регулятором, является функцией состояния ОУ. Если все переменные вектора состояния ОУ доступны для измерения, то говорят об объекте управления с полной информацией. В этом случае регулятор вырабатывает закон управления как линейную функцию состояний.
 (3)
(3)
К - матрица линейных стационарных обратных связей (ЛСОС) по состояниям ОУ.
Если не все компоненты вектора состояний измеримы, в этом случае
располагают объектом управления с неполной информацией и для реализации закона
управления используют оценки состояний ОУ, и закон
управления приобретает вид:
состояний ОУ, и закон
управления приобретает вид:
 (4)
(4)
Регулятор, вырабатывающий закон управления (4), называют динамическим регулятором, поскольку для получения оценок состояния ОУ в структуру регулятора вводят дополнительные динамические звенья.
Под модальным управлением понимается изменение собственных движений замкнутой системы, а, следовательно, и полюсов системы с помощью управляющих воздействий с целью достижения требуемых показателей качества. При модальном синтезе проектируется ООС по переменным состояния таким образом, чтобы полюса системы находились в наперед заданной области и расположение которых определяло бы необходимое качество управления. Связь полюсов замкнутой системы с требуемыми показателями качества основывается на использовании стандартных полиномов, определяющих коэффициенты характеристического уравнения проектируемой системы. Стандартные полиномы задают эталонную модель системы, обладающую желаемыми показателями качества. Поэтому синтез регуляторов с помощью метода модальных управлений состоит в задании эталонной модели с желаемыми свойствами и нахождении матрицы ЛСОС по состояниям ОУ - закона управления, обеспечивающего в замкнутой системе те же самые полюса, что и в эталонной модели.
Для синтеза модального регулятора по изложенной методике зададимся эталонной моделью с биноминальным распределением корней характеристического уравнения, поскольку желаемый переходной процесс в этом случае протекает без перерегулирования.
Для системы четвертого порядка характеристическое уравнение эталонной модели определяется выражением:
 (5)
(5)

Синтез эстиматора состояния
При решении практических задач управления методами теории пространства состояний часто встречаются случаи, когда-либо все переменные состояния, либо часть компонент вектора состояния оказываются неизмеримыми. Для того чтобы воспользоваться теорией модального управления для таких объектов, необходимо оценивать неизмеримые состояния объекта по его измеримым входным и выходным координатам.
Если в следящей системе одна из компонент вектора состояния измерима и известна, то оставшиеся переменные состояния можно восстановить с помощью детерминированного эстиматора состояния пониженного порядка.
В общем случае векторно-матричное уравнение динамики эстиматора имеет вид:
 (6)
(6)
В качестве желаемых полюсов эстиматора зададим корни характеристического полинома. При этом эстиматор должен вести себя хотя бы в пять раз быстрее чем сама замкнутая система, то есть апериодический переходный процесс для эстиматора должен быть завершен примерно за время равное трем шагам дискретности системы. Этого результата можно добиться в том случае если корни характеристического полинома будут равны нулю, тогда апериодический процесс будет окончен за количество шагов равное размерности эстиматора. В веду выше сказанного, для характеристического полинома эстиматора зададим три нулевых корня z1=z2=z3=0.
Чтобы проанализировать точность расчета наблюдающего устройства, сопоставим точные значения компонент вектора состояния дискретной следящей системы и оценки, полученные в соответствии с выведенными уравнениями наблюдателя.
Ниже представлены графики динамики переменных состояния объекта управления, восстанавливаемых при помощи спроектированного эстиматора.
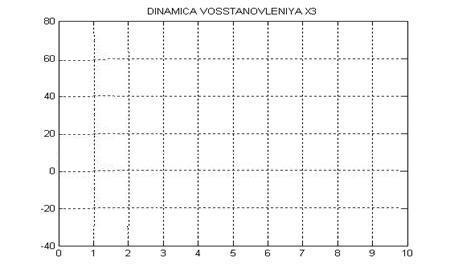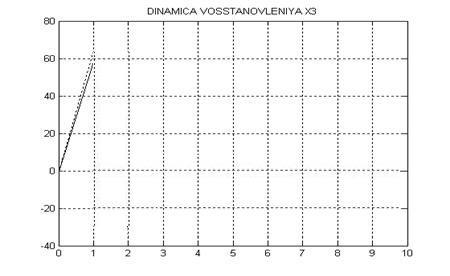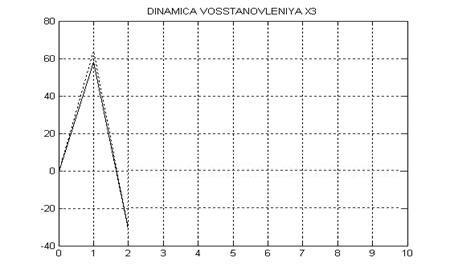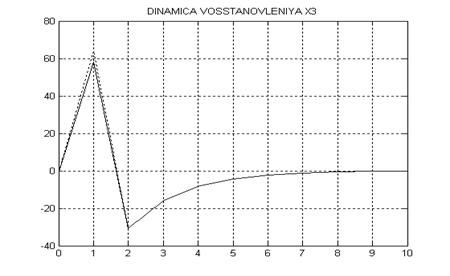
Рисунок 4 – Динамика восстановления компоненты x3

Исследование объекта с динамическим регулятором
Спроектированный в данной работе динамический регулятор для следящей системы привода шарнира манипулятора включает в свой состав модальный регулятор и эстиматор состояния. Структурная схема системы регулирования с динамическим регулятором представлена на рис. 5.
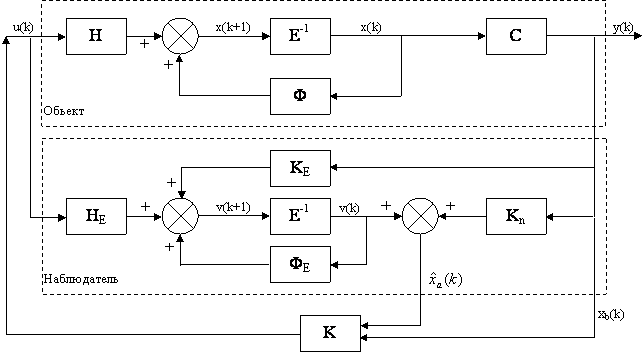
Рисунок 5 – Управляемый объект с динамическим регулятором
Исследование динамических свойств регулятора проведем путем оценки влияния изменений некоторых параметров системы на поведение переходной характеристики, при постоянных параметрах динамического регулятора.
Основными изменяющимися параметрами при работе робота манипулятора являются: момент инерции, изменяющийся вследствие изменения кинематики манипулятора и взаимного влияния его звеньев, коэффициент вязкого трения, увеличение которого обусловлено износом подшипников, а также время дискретности системы, зависящее от частоты считывания данных с датчика угла поворота.
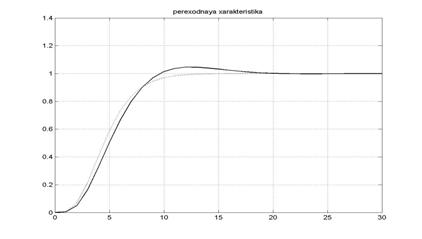
Рисунок 6 - Переходная характеристика при увеличении J на 50 %
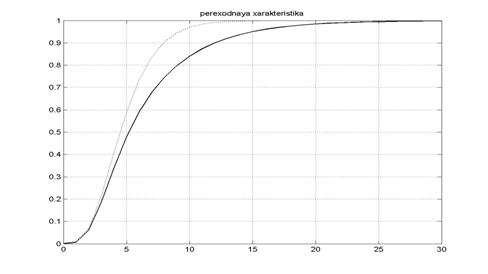
Рисунок 7 - Переходная характеристика при увеличении f на 50 %
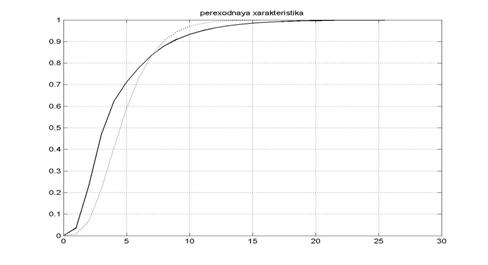
Рисунок 8 – Переходная характеристика при увеличении T в 2.5 рази и увеличении f на 100%
Рассмотренная в данной работе следящая система привода шарнира робота манипулятора как объект управления описывается уравнениями 4-го порядка. Система является одномерной, то есть имеет один вход и один выход в виде угла поворота звена манипулятора.
Для того чтобы следящая система имела необходимые для управления роботом манипулятором показатели качества, то есть управление велось с минимально возможным перерегулированием и заданным временем регулирования, синтезирован динамический регулятор, включающий в свою структуру модальный регулятор в виде матрицы линейных стационарных обратных связей по переменным состояния объекта и эстиматор состояния. Полученная таким образом система управления имеет удовлетворяющие поставленной задаче показатели, а именно время регулирования менее заданного 140 мсек. и перерегулирование близкое к нулю.
Эстиматор состояния позволяет оценить неизмеримые переменные состояния объекта. Уравнение эстиматора найдено по желаемому расположению его корней, которые выбраны равными нулю из соображений, что при таких корнях эстиматор является достаточно быстродействующим, что позволяет восстанавливать переменные состояния с достаточной точностью уже за время равное 3...5 интервалам дискретности объекта управления.
Анализ следящей системы с динамическим регулятором проведен путем оценки поведения выходной координаты системы - угла поворота звена манипулятора, при отклонении некоторых параметров системы от расчетных значений.
Так при изменении момента инерции, обусловленного постоянным взаимодействием звеньев между собой в ходе движения манипулятора, видно, что при увеличении момента инерции повышается величина перерегулирования, а при его уменьшении перерегулирование не возникает, но в обоих случаях длительность переходного процесса возрастает. Из анализа можно сказать, что данная система будет удовлетворять требованиям предъявляемым к следящим системам роботов манипуляторов, если отклонение момента инерции от расчетного значения не будет превышать во всем диапазоне движений 50 %. При таких значениях момента инерции можно говорить, что к концу интервала времени, ограниченного необходимым временем регулирования, статическая ошибка будет невелика и может быть устранена на этапе точного управления роботом манипулятором.
Увеличение значения такого показателя, как коэффициент вязкого трения, обусловленного износом подшипников, приводит к затягиванию переходных процессов во времени, при увеличении коэффициента вязкого трения на 50 % увеличение времени регулирования становится явно больше необходимого. Таким образом влияние на динамику системы, оказываемое изменением коэффициента вязкого трения значительно больше в сравнении с влиянием оказываемым изменением момента инерции, что позволяет говорить о повышенной критичности этого параметра и недопустимости значительного его отклонения.
Увеличение интервала дискретности системы, связанное с периодом опроса датчика угла поворота, позволяет сделать систему менее чувствительной к различного рода внешним возмущениям. В этом случае переходная характеристика ведет себя более быстротечно, хотя и приобретает некоторую колебательность.
На даный момент работа является не завершенной. В ближайшем будущем планируется добавить пункт "Робастное управление".

Перечень ссылок
1.
Фу, Кисан и др. Робототехника. М,: Мир 1989г.
2.
Шахинпур, Мозен. Курс робототехники. М.: Мир 1990 г.
3.
В.Г. Домрачев В.Р. Матвеевский и др. Схемотехника цифровых преобразователей перемещениям.: Машиностроение 1987г.
4.
Синтез дискретных регуляторов при помощи ЭВМ / В.В. Григорьев, В.Н.
Дроздов, В.В. Лаврентьев, А.В. Ушаков. Л.: Машиностроение 1983 г.
5.
К.И. Палк. Системы управления механической обработкой на станках Л. : Машиностроение 1984 г.
6.
Н.Т. Кузовков. Модальное управление и наблюдающие устройства. М. : Машиностроение 1976 г.
7.
Н. И. Соколов. Аналитический метод синтеза линеаризованных систем автоматического регулирования. М.: Машиностроение 1966 г.
8.
Стрейц В. Метод пространства состояний в теории дискретных линейных систем управления. - М.: Наука, 1985г.






